Question Number 104115 by bobhans last updated on 19/Jul/20
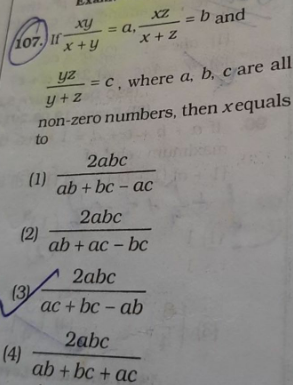
Answered by nimnim last updated on 19/Jul/20

$$\frac{{xy}}{{x}+{y}}={a},\:\frac{{xz}}{{x}+{z}}={b},\:\frac{{yz}}{{y}+{z}}={c} \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}=\frac{\mathrm{1}}{{a}},\:\:\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{z}}=\frac{\mathrm{1}}{{b}},\:\:\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}=\frac{\mathrm{1}}{{c}} \\ $$$$\mathrm{2}\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}\right)=\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}=\frac{{bc}+{ac}+{ab}}{{abc}} \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{c}}=\frac{{bc}+{ac}+{ab}}{\mathrm{2}{abc}} \\ $$$$\frac{\mathrm{1}}{{x}}=\frac{{bc}+{ac}+{ab}}{\mathrm{2}{abc}}−\frac{\mathrm{1}}{{c}} \\ $$$$\frac{\mathrm{1}}{{x}}=\frac{{bc}+{ac}+{ab}−\mathrm{2}{ab}}{\mathrm{2}{abc}}=\frac{{bc}+{ac}−{ab}}{\mathrm{2}{abc}} \\ $$$${x}=\frac{\mathrm{2}{abc}}{{ac}+{bc}−{ab}} \\ $$
Commented by bemath last updated on 19/Jul/20

$${colll} \\ $$
Commented by bobhans last updated on 19/Jul/20

$${nice}\:! \\ $$
