Question Number 104207 by PengagumRahasiamu last updated on 20/Jul/20

Answered by bemath last updated on 20/Jul/20
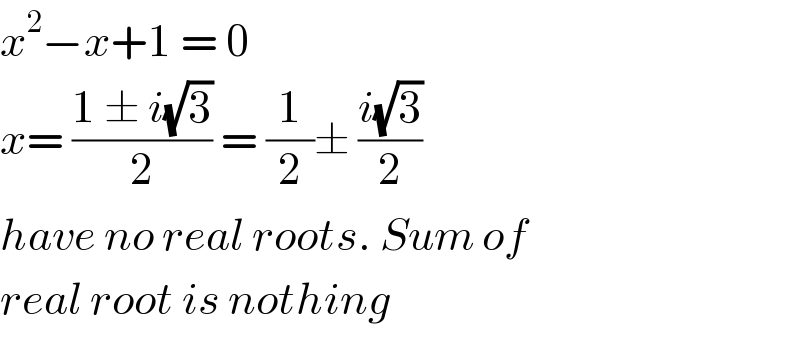
$${x}^{\mathrm{2}} −{x}+\mathrm{1}\:=\:\mathrm{0} \\ $$$${x}=\:\frac{\mathrm{1}\:\pm\:{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\pm\:\frac{{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${have}\:{no}\:{real}\:{roots}.\:{Sum}\:{of} \\ $$$${real}\:{root}\:{is}\:{nothing} \\ $$
Answered by OlafThorendsen last updated on 20/Jul/20

$$\mathrm{if}\:\mathrm{a}\:\mathrm{root}\:\mathrm{is}\:{z}\:=\:\alpha+{i}\beta \\ $$$$\mathrm{the}\:\mathrm{second}\:\mathrm{root}\:\mathrm{is}\:\overset{\_} {{z}}\:=\:\alpha−{i}\beta \\ $$$$\mathrm{The}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{its}\:\mathrm{real}\:\mathrm{root}\:\mathrm{is} \\ $$$${z}+\overset{\_} {{z}}\:=\:\mathrm{2}\alpha \\ $$$$\mathrm{In}\:\mathrm{fact}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{is}\:−\frac{{b}}{{a}}\:=\:−\frac{−\mathrm{1}}{\mathrm{1}} \\ $$$$\mathrm{So}\:{z}+\overset{\_} {{z}}\:=\:\mathrm{1} \\ $$$$\mathrm{but}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{not}\:\mathrm{clear} \\ $$$$\mathrm{you}\:\mathrm{should}\:\mathrm{answer}\:“\mathrm{nothing}'' \\ $$
