Question Number 104281 by ajfour last updated on 20/Jul/20
Commented by ajfour last updated on 20/Jul/20

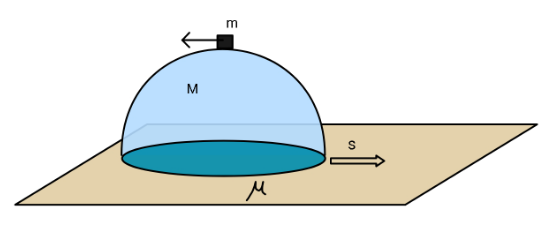
$${How}\:{far}\:\left({s}=?\right)\:{can}\:{the} \\ $$$${hemisphere}\:{slide}\:{if}\:{a}\:{block}\:{of} \\ $$$${mass}\:{m}\:{placed}\:{atop}\:{it}\:{is}\:{given}\:{a} \\ $$$${gentle}\:{tap}\:{towards}\:{left}. \\ $$$${Assume}\:{no}\:{friction}\:{between}\:{block} \\ $$$${and}\:{hemisphere},\:{but}\:{friction} \\ $$$${coefficient}\:\boldsymbol{\mu}\:{between}\:{ground}\:{and} \\ $$$${hemisphere}\:\left({solid}\right). \\ $$$$\left({Also}\:{assume}\:{that}\:{hemisphere}\right. \\ $$$${starts}\:{sliding}\:{before}\:{block}\:{breaks} \\ $$$$\left.{contact}\:{with}\:{the}\:{hemisphere}\right). \\ $$
Answered by mr W last updated on 20/Jul/20
Commented by mr W last updated on 21/Jul/20
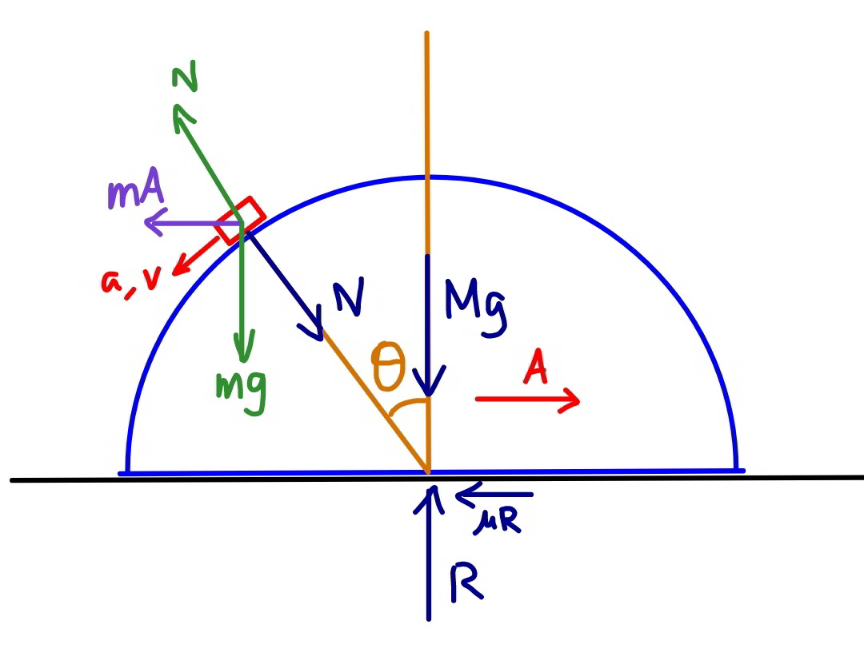
![ω=(dθ/dt) v=ωr mω^2 r=mg cos θ−N−mA sin θ ⇒N=m(g cos θ−A sin θ−ω^2 r) R=Mg+N cos θ N sin θ−μR=MA N sin θ−μ(Mg+N cos θ)=MA N(sin θ−μ cos θ)−μMg=MA (m/M)(g cos θ−ω^2 r−A sin θ)(sin θ−μ cos θ)−μg=A ⇒(m/M)(g cos θ−ω^2 r)(sin θ−μ cos θ)−μg=A[1+sin θ(sin θ−μ cos θ)] mg sin θ+mA cos θ=mr(dω/dt) (dω/dt)=ω(dω/dθ) ⇒A=(rω(dω/dθ)−g sin θ)(1/(cos θ)) ⇒(m/M)(cos θ−(r/g)ω^2 )(sin θ−μ cos θ)−μ =((r/g)ω(dω/dθ)−sin θ)((1+sin θ(sin θ−μ cos θ))/(cos θ)) ⇒ω=f(θ).....not really possible to solve ......](https://www.tinkutara.com/question/Q104334.png)
$$\omega=\frac{{d}\theta}{{dt}} \\ $$$${v}=\omega{r} \\ $$$${m}\omega^{\mathrm{2}} {r}={mg}\:\mathrm{cos}\:\theta−{N}−{mA}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow{N}={m}\left({g}\:\mathrm{cos}\:\theta−{A}\:\mathrm{sin}\:\theta−\omega^{\mathrm{2}} {r}\right) \\ $$$${R}={Mg}+{N}\:\mathrm{cos}\:\theta \\ $$$${N}\:\mathrm{sin}\:\theta−\mu{R}={MA} \\ $$$${N}\:\mathrm{sin}\:\theta−\mu\left({Mg}+{N}\:\mathrm{cos}\:\theta\right)={MA} \\ $$$${N}\left(\mathrm{sin}\:\theta−\mu\:\mathrm{cos}\:\theta\right)−\mu{Mg}={MA} \\ $$$$\frac{{m}}{{M}}\left({g}\:\mathrm{cos}\:\theta−\omega^{\mathrm{2}} {r}−{A}\:\mathrm{sin}\:\theta\right)\left(\mathrm{sin}\:\theta−\mu\:\mathrm{cos}\:\theta\right)−\mu{g}={A} \\ $$$$\Rightarrow\frac{{m}}{{M}}\left({g}\:\mathrm{cos}\:\theta−\omega^{\mathrm{2}} {r}\right)\left(\mathrm{sin}\:\theta−\mu\:\mathrm{cos}\:\theta\right)−\mu{g}={A}\left[\mathrm{1}+\mathrm{sin}\:\theta\left(\mathrm{sin}\:\theta−\mu\:\mathrm{cos}\:\theta\right)\right] \\ $$$${mg}\:\mathrm{sin}\:\theta+{mA}\:\mathrm{cos}\:\theta={mr}\frac{{d}\omega}{{dt}} \\ $$$$\frac{{d}\omega}{{dt}}=\omega\frac{{d}\omega}{{d}\theta} \\ $$$$\Rightarrow{A}=\left({r}\omega\frac{{d}\omega}{{d}\theta}−{g}\:\mathrm{sin}\:\theta\right)\frac{\mathrm{1}}{\mathrm{cos}\:\theta} \\ $$$$\Rightarrow\frac{{m}}{{M}}\left(\mathrm{cos}\:\theta−\frac{{r}}{{g}}\omega^{\mathrm{2}} \right)\left(\mathrm{sin}\:\theta−\mu\:\mathrm{cos}\:\theta\right)−\mu \\ $$$$\:\:\:=\left(\frac{{r}}{{g}}\omega\frac{{d}\omega}{{d}\theta}−\mathrm{sin}\:\theta\right)\frac{\mathrm{1}+\mathrm{sin}\:\theta\left(\mathrm{sin}\:\theta−\mu\:\mathrm{cos}\:\theta\right)}{\mathrm{cos}\:\theta} \\ $$$$\Rightarrow\omega={f}\left(\theta\right)…..{not}\:{really}\:{possible}\:{to}\:{solve} \\ $$$$…… \\ $$
Commented by mr W last updated on 21/Jul/20
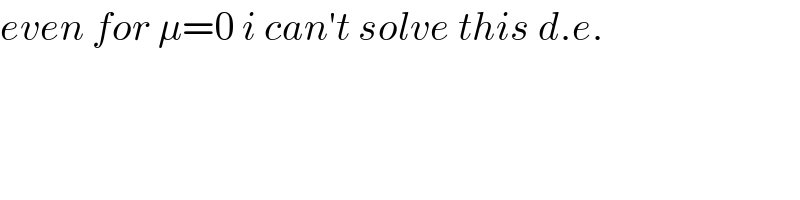
$${even}\:{for}\:\mu=\mathrm{0}\:{i}\:{can}'{t}\:{solve}\:{this}\:{d}.{e}. \\ $$
