Question Number 104302 by bobhans last updated on 20/Jul/20
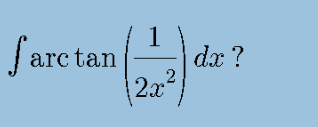
Commented by bobhans last updated on 21/Jul/20

$${by}\:{parts} \\ $$$$\begin{cases}{{u}=\mathrm{arc}\:\mathrm{tan}\:\left(\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\right)\:\Rightarrow{du}\:=\frac{−\frac{\mathrm{1}}{{x}^{\mathrm{3}} }}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}{x}^{\mathrm{4}} }}\:{dx}}\\{{dv}\:=\:{dx}\:\Rightarrow{v}\:=\:{x}}\end{cases} \\ $$$${I}=\:{x}\:\mathrm{arc}\:\mathrm{tan}\:\left(\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\right)+\int\:\frac{\mathrm{4}{x}^{\mathrm{2}} }{\mathrm{4}{x}^{\mathrm{4}} +\mathrm{1}}\:{dx} \\ $$$${I}=\:{x}\:\mathrm{arctan}\:\left(\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\right)\:+\int\:\frac{{x}}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}−\frac{{x}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}}\:{dx} \\ $$$$ \\ $$
Commented by john santu last updated on 20/Jul/20
![I= x tan^(−1) ((1/(2x^2 )))+∫(x/(2x^2 −2x+1))−(x/(2x^2 +2x+1))dx let J= ∫((2x)/(4x^2 −4x+2))−((2x)/(4x^2 +4x+2))dx J= ∫ ((2x)/((2x−1)^2 +1))−((2x)/((2x+1)^2 +1))dx J=∫((2x−1+1)/((2x−1)^2 +1))−((2x+1−1)/((2x+1)^2 +1))dx J=∫ [((2x−1)/((2x−1)^2 +1))+(1/((2x−1)^2 +1))−((2x+1)/((2x+1)^2 +1))+(1/((2x+1)^2 +1))]dx J= (1/2)ln ∣((2x^2 −2x+1)/(2x^2 +2x+1))∣ +(1/2){tan^(−1) (2x−1)+tan^(−1) (2x−1)} we conclude I= x tan^(−1) ((1/(2x^2 )))+(1/2)ln ∣((2x^2 −2x+1)/(2x^2 +2x+1))∣+ (1/2){tan^(−1) (2x−1)+tan^(−1) (2x+1)} + C (JS ⊛)](https://www.tinkutara.com/question/Q104337.png)
$${I}=\:{x}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\right)+\int\frac{{x}}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}−\frac{{x}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}}{dx} \\ $$$${let}\:{J}=\:\int\frac{\mathrm{2}{x}}{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{2}}−\frac{\mathrm{2}{x}}{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{2}}{dx} \\ $$$${J}=\:\int\:\frac{\mathrm{2}{x}}{\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{2}{x}}{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$${J}=\int\frac{\mathrm{2}{x}−\mathrm{1}+\mathrm{1}}{\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{2}{x}+\mathrm{1}−\mathrm{1}}{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$${J}=\int\:\left[\frac{\mathrm{2}{x}−\mathrm{1}}{\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{1}}{\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{2}{x}+\mathrm{1}}{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{1}}{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}\right]{dx} \\ $$$${J}=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}}\mid\:+\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}{x}−\mathrm{1}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}{x}−\mathrm{1}\right)\right\} \\ $$$${we}\:{conclude}\: \\ $$$${I}=\:{x}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}}\mid+ \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}{x}−\mathrm{1}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}{x}+\mathrm{1}\right)\right\}\:+\:{C} \\ $$$$\left({JS}\:\circledast\right)\: \\ $$
Answered by OlafThorendsen last updated on 20/Jul/20

$$\mathrm{arctan}{u}+\mathrm{arctan}\frac{\mathrm{1}}{{u}}\:=\:\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{I}\:=\:\int\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\right){dx} \\ $$$$\mathrm{I}\:=\:\frac{\pi}{\mathrm{2}}{x}−\int\mathrm{arctan}\left(\mathrm{2}{x}^{\mathrm{2}} \right){dx} \\ $$$$\mathrm{I}\:=\:\frac{\pi}{\mathrm{2}}{x}−{x}\mathrm{arctan}\left(\mathrm{2}{x}^{\mathrm{2}} \right)+\int\frac{\mathrm{4}{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{4}{x}^{\mathrm{4}} }{dx} \\ $$$$… \\ $$
Commented by Ar Brandon last updated on 20/Jul/20
![Cool !!! Mind if I continue... J=∫((4x^2 )/(1+4x^4 ))dx=∫{((2x^2 +1)/(4x^4 +1))+((2x^2 −1)/(4x^4 +1))}dx =∫{((2+(1/x^2 ))/(4x^2 +(1/x^2 )))+((2−(1/x^2 ))/(4x^2 +(1/x^2 )))}dx=∫{((2+(1/x^2 ))/((2x−(1/x))^2 +4))+((2−(1/x^2 ))/((2x+(1/x))^2 −4))}dx =(1/2)Arctan[((2x^2 −1)/(2x))]−(1/2)Arctanh[((2x^2 +1)/(2x))]+C](https://www.tinkutara.com/question/Q104314.png)
$$\mathrm{Cool}\:!!!\:\:\mathrm{Mind}\:\mathrm{if}\:\mathrm{I}\:\mathrm{continue}… \\ $$$$\mathrm{J}=\int\frac{\mathrm{4}{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{4}{x}^{\mathrm{4}} }\mathrm{d}{x}=\int\left\{\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{4}{x}^{\mathrm{4}} +\mathrm{1}}+\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{4}{x}^{\mathrm{4}} +\mathrm{1}}\right\}\mathrm{d}{x} \\ $$$$\:\:=\int\left\{\frac{\mathrm{2}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\mathrm{4}{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}+\frac{\mathrm{2}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\mathrm{4}{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\right\}\mathrm{d}{x}=\int\left\{\frac{\mathrm{2}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\left(\mathrm{2}{x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{4}}+\frac{\mathrm{2}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\left(\mathrm{2}{x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{4}}\right\}\mathrm{d}{x} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Arctan}\left[\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{x}}\right]−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Arctanh}\left[\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{x}}\right]+\mathcal{C} \\ $$
Answered by Dwaipayan Shikari last updated on 20/Jul/20
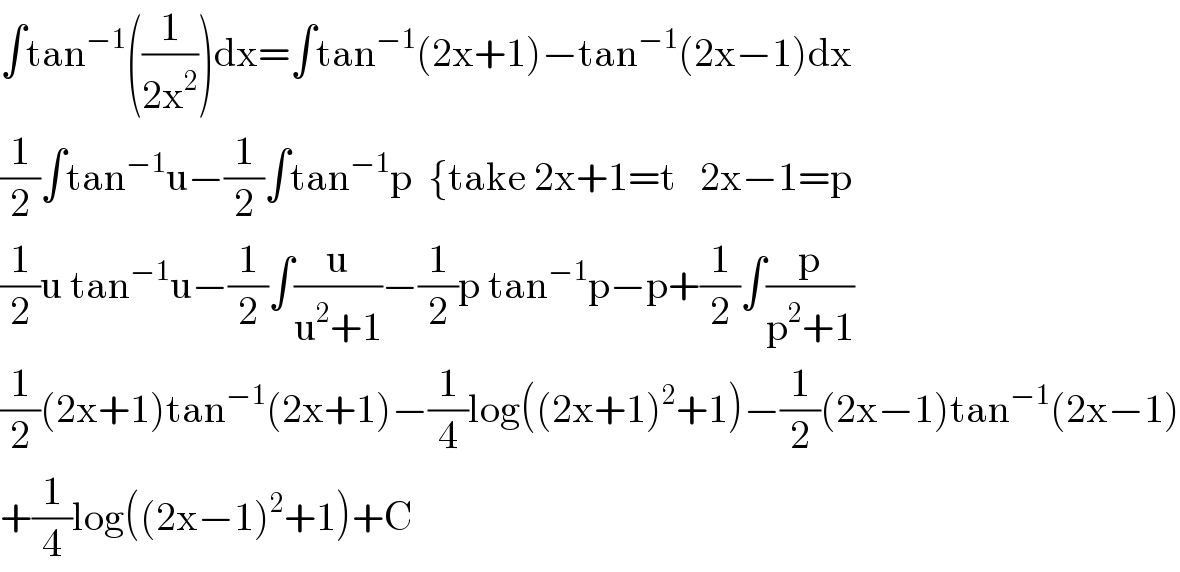
$$\int\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2x}^{\mathrm{2}} }\right)\mathrm{dx}=\int\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2x}+\mathrm{1}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2x}−\mathrm{1}\right)\mathrm{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{tan}^{−\mathrm{1}} \mathrm{u}−\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{tan}^{−\mathrm{1}} \mathrm{p}\:\:\left\{\mathrm{take}\:\mathrm{2x}+\mathrm{1}=\mathrm{t}\:\:\:\mathrm{2x}−\mathrm{1}=\mathrm{p}\right. \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{u}\:\mathrm{tan}^{−\mathrm{1}} \mathrm{u}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{u}}{\mathrm{u}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{p}\:\mathrm{tan}^{−\mathrm{1}} \mathrm{p}−\mathrm{p}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{p}}{\mathrm{p}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2x}+\mathrm{1}\right)\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2x}+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{log}\left(\left(\mathrm{2x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2x}−\mathrm{1}\right)\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2x}−\mathrm{1}\right) \\ $$$$+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{log}\left(\left(\mathrm{2x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\right)+\mathrm{C} \\ $$
Commented by Ar Brandon last updated on 20/Jul/20
wow ! that was creative ��
Commented by Dwaipayan Shikari last updated on 20/Jul/20
Sir olaftheorendsen , gives me this idea. ��
Answered by mathmax by abdo last updated on 21/Jul/20

$$\mathrm{A}\:=\int\:\:\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{2x}^{\mathrm{2}} }\right)\mathrm{dx}\:\:\:\Rightarrow\mathrm{A}=\:\int\left(\frac{\pi}{\mathrm{2}}−\mathrm{arctan}\left(\mathrm{2x}^{\mathrm{2}} \right)\right)\mathrm{dx} \\ $$$$\mathrm{A}\:=\frac{\pi\mathrm{x}}{\mathrm{2}}\:−\int\:\mathrm{arctan}\left(\mathrm{2x}^{\mathrm{2}} \right)\mathrm{dx}\:\:\mathrm{by}\:\mathrm{parts}\:\mathrm{u}^{'} \:=\mathrm{1}\:\mathrm{and}\:\mathrm{v}\:=\mathrm{arctan}\left(\mathrm{2x}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$$\int\:\mathrm{arctan}\left(\mathrm{2x}^{\mathrm{2}} \right)\mathrm{dx}\:=\mathrm{x}\:\mathrm{arctan}\left(\mathrm{2x}^{\mathrm{2}} \right)−\int\:\mathrm{x}.\frac{\mathrm{4x}}{\mathrm{1}+\mathrm{4x}^{\mathrm{4}} }\mathrm{dx} \\ $$$$=\mathrm{xarctan}\left(\mathrm{2x}^{\mathrm{2}} \right)−\mathrm{4}\:\int\:\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{4x}^{\mathrm{4}} }\:\mathrm{dx}\:\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4x}^{\mathrm{4}} \:+\mathrm{1}}\mathrm{dx}\:=\int\:\:\frac{\mathrm{x}^{\mathrm{2}} }{\left(\sqrt{\mathrm{2}}\mathrm{x}\right)^{\mathrm{4}} \:+\mathrm{1}}\:=_{\sqrt{\mathrm{2}}\mathrm{x}\:=\mathrm{t}} \:\:\:\:\int\:\:\:\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{t}^{\mathrm{4}} \:+\mathrm{1}\right)}\:\frac{\mathrm{dt}}{\:\sqrt{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int\:\:\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{4}} \:+\mathrm{1}}\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int\:\:\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\:\int\:\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\mathrm{t}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}\:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\:\int\:\:\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\left(\mathrm{t}+\frac{\mathrm{1}}{\mathrm{t}}\right)^{\mathrm{2}} −\mathrm{2}}\mathrm{dt}\left(\rightarrow\mathrm{u}\:=\mathrm{t}+\frac{\mathrm{1}}{\mathrm{t}}\right)+\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\:\int\:\:\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\left(\mathrm{t}−\frac{\mathrm{1}}{\mathrm{t}}\right)^{\mathrm{2}} +\mathrm{2}}\mathrm{dt}\left(\rightarrow\mathrm{v}\:=\mathrm{t}−\frac{\mathrm{1}}{\mathrm{t}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\:\int\:\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} −\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\:\int\:\frac{\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} \:+\mathrm{2}}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int\:\:\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} −\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int\left(\frac{\mathrm{1}}{\mathrm{u}−\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{u}+\sqrt{\mathrm{2}}}\right)\mathrm{du}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\mid\frac{\mathrm{u}−\sqrt{\mathrm{2}}}{\mathrm{u}+\sqrt{\mathrm{2}}}\mid+\mathrm{c}_{\mathrm{1}} \:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\mid\frac{\mathrm{t}+\frac{\mathrm{1}}{\mathrm{t}}−\sqrt{\mathrm{2}}}{\mathrm{t}+\frac{\mathrm{1}}{\mathrm{t}}+\sqrt{\mathrm{2}}}\mid+\mathrm{c}_{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\mid\frac{\sqrt{\mathrm{2}}\mathrm{x}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\mathrm{x}}−\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}\mathrm{x}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\mathrm{x}}+\sqrt{\mathrm{2}}}\mid\:+\mathrm{c}_{\mathrm{1}} \\ $$$$\int\:\frac{\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} \:+\mathrm{2}}\:=_{\mathrm{v}=\sqrt{\mathrm{2}}\mathrm{z}} \:\:\:\int\:\:\frac{\sqrt{\mathrm{2}}\mathrm{dz}}{\mathrm{2}\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)}\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\mathrm{arctanz}\:+\mathrm{c}_{\mathrm{2}} =\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\mathrm{arctan}\left(\frac{\mathrm{v}}{\:\sqrt{\mathrm{2}}}\right)\:+\mathrm{c}_{\mathrm{2}} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left\{\sqrt{\mathrm{2}}\mathrm{x}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\mathrm{x}}\right\}\right)\:+\mathrm{c}_{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{A}\:=\mathrm{x}\:\mathrm{arctan}\left(\mathrm{2x}^{\mathrm{2}} \right)−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left\{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\mid\frac{\mathrm{2x}^{\mathrm{2}} +\mathrm{1}−\mathrm{2x}}{\mathrm{2x}^{\mathrm{2}} +\mathrm{1}+\mathrm{2x}}\mid\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\mathrm{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\sqrt{\mathrm{2}}\mathrm{x}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\mathrm{x}}\right)\right)\:+\mathrm{C}\right. \\ $$$$\mathrm{A}\:=\mathrm{xarctan}\left(\mathrm{2x}^{\mathrm{2}} \right)−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\mid\frac{\mathrm{2x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}}{\mathrm{2x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{1}}\mid−\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{arctan}\left\{\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2x}}\right\}\:+\mathrm{C} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 21/Jul/20
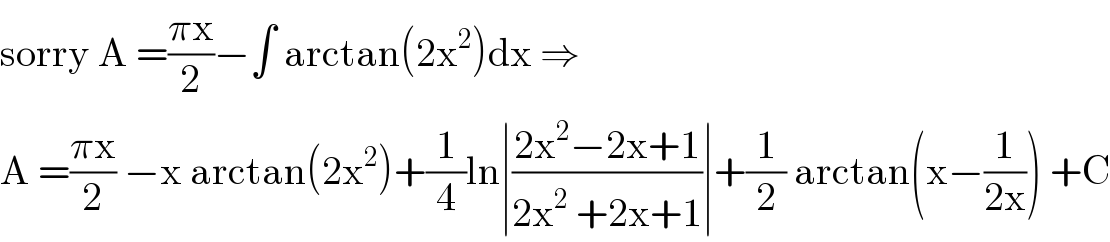
$$\mathrm{sorry}\:\mathrm{A}\:=\frac{\pi\mathrm{x}}{\mathrm{2}}−\int\:\mathrm{arctan}\left(\mathrm{2x}^{\mathrm{2}} \right)\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{A}\:=\frac{\pi\mathrm{x}}{\mathrm{2}}\:−\mathrm{x}\:\mathrm{arctan}\left(\mathrm{2x}^{\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\mid\frac{\mathrm{2x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}}{\mathrm{2x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{1}}\mid+\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{arctan}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2x}}\right)\:+\mathrm{C} \\ $$
