Question Number 104364 by ajfour last updated on 21/Jul/20

Commented by ajfour last updated on 21/Jul/20

$${Find}\:{the}\:{area}\:{of}\:{the}\:\bigtriangleup{CGI}\:; \\ $$$${C}\:{is}\:{circumcentre}\:{of}\:\bigtriangleup{PQR}, \\ $$$${G}\:{its}\:{centroid}\:{and}\:{I}\:{its}\:{incentre}. \\ $$
Answered by mr W last updated on 21/Jul/20
![c=(√(a^2 +b^2 )) radius of incircle r (((a+b+c)r)/2)=((ab)/2) ⇒r=((ab)/(a+b+c)) G((a/3),(b/3)) I(r,r) C((a/2),(b/2)) A_(ΔGCI) =(1/2)∣ determinant ((((a/2)−(a/3)),((b/2)−(b/3))),(((a/2)−r),((b/2)−r)))∣ =(1/2)∣[(a/6)((b/2)−r)−(b/6)((a/2)−r)]∣ =((ab∣a−b∣)/(12(a+b+(√(a^2 +b^2 )))))](https://www.tinkutara.com/question/Q104372.png)
$${c}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${radius}\:{of}\:{incircle}\:{r} \\ $$$$\frac{\left({a}+{b}+{c}\right){r}}{\mathrm{2}}=\frac{{ab}}{\mathrm{2}} \\ $$$$\Rightarrow{r}=\frac{{ab}}{{a}+{b}+{c}} \\ $$$${G}\left(\frac{{a}}{\mathrm{3}},\frac{{b}}{\mathrm{3}}\right) \\ $$$${I}\left({r},{r}\right) \\ $$$${C}\left(\frac{{a}}{\mathrm{2}},\frac{{b}}{\mathrm{2}}\right) \\ $$$${A}_{\Delta{GCI}} =\frac{\mathrm{1}}{\mathrm{2}}\mid\begin{vmatrix}{\frac{{a}}{\mathrm{2}}−\frac{{a}}{\mathrm{3}}}&{\frac{{b}}{\mathrm{2}}−\frac{{b}}{\mathrm{3}}}\\{\frac{{a}}{\mathrm{2}}−{r}}&{\frac{{b}}{\mathrm{2}}−{r}}\end{vmatrix}\mid \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mid\left[\frac{{a}}{\mathrm{6}}\left(\frac{{b}}{\mathrm{2}}−{r}\right)−\frac{{b}}{\mathrm{6}}\left(\frac{{a}}{\mathrm{2}}−{r}\right)\right]\mid \\ $$$$=\frac{{ab}\mid{a}−{b}\mid}{\mathrm{12}\left({a}+{b}+\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right)} \\ $$
Commented by mr W last updated on 21/Jul/20

$${yes},\:{thanks}! \\ $$
Commented by ajfour last updated on 21/Jul/20
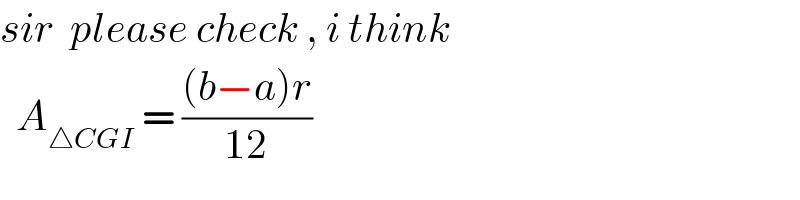
$${sir}\:\:{please}\:{check}\:,\:{i}\:{think} \\ $$$$\:\:{A}_{\bigtriangleup{CGI}} \:=\:\frac{\left({b}−{a}\right){r}}{\mathrm{12}} \\ $$
Answered by ajfour last updated on 21/Jul/20

$${let}\:{Q}\:{be}\:{origin}. \\ $$$${R}\left({a},\mathrm{0}\right)\:;\:\:{P}\left(\mathrm{0},{b}\right)\:\: \\ $$$${x}_{{I}} \:=\frac{{ax}_{\mathrm{1}} +{bx}_{\mathrm{2}} +{cx}_{\mathrm{3}} }{{a}+{b}+{c}}\: \\ $$$$\:\:\:\:=\:\frac{{a}×\mathrm{0}+{b}×{a}+{c}×\mathrm{0}}{{a}+{b}+{c}}\:=\frac{{ab}}{{a}+{b}+{c}} \\ $$$${y}_{{I}} \:=\:\frac{{ay}_{\mathrm{1}} +{by}_{\mathrm{2}} +{cy}_{\mathrm{3}} }{{a}+{b}+{c}}\:=\:\frac{{ab}}{{a}+{b}+{c}} \\ $$$$\:\:{G}\left(\frac{{a}}{\mathrm{3}},\frac{{b}}{\mathrm{3}}\right)\:\:\:;\:\:{C}\left(\frac{{a}}{\mathrm{2}},\frac{{b}}{\mathrm{2}}\right) \\ $$$${Area}\:\bigtriangleup{CGI}\:=\frac{\mathrm{1}}{\mathrm{2}}\begin{vmatrix}{\frac{{a}}{\mathrm{2}}}&{\frac{{b}}{\mathrm{2}}}&{\mathrm{1}}\\{\frac{{a}}{\mathrm{3}}}&{\frac{{b}}{\mathrm{3}}}&{\mathrm{1}}\\{\frac{{ab}}{{a}+{b}+{c}}}&{\frac{{ab}}{{a}+{b}+{c}}}&{\mathrm{1}}\end{vmatrix} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\frac{{a}}{\mathrm{2}}\left(\frac{{b}}{\mathrm{3}}−{r}\right)−\frac{{b}}{\mathrm{2}}\left(\frac{{a}}{\mathrm{3}}−{r}\right)\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{r}\left(\frac{{a}}{\mathrm{3}}−\frac{{b}}{\mathrm{3}}\right)\right\} \\ $$$$\:\:\:=\:\frac{{r}}{\mathrm{2}}\left(\frac{{b}}{\mathrm{6}}−\frac{{a}}{\mathrm{6}}\right)\:=\:\frac{{r}\left({b}−{a}\right)}{\mathrm{12}} \\ $$$$\:\bigtriangleup_{{CGI}} \:=\:\frac{{ab}\left({b}−{a}\right)}{\mathrm{12}\left({a}+{b}+\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right)}\:\bigstar \\ $$
