Question Number 104369 by quvonchbek3737 last updated on 21/Jul/20

Answered by mr W last updated on 21/Jul/20
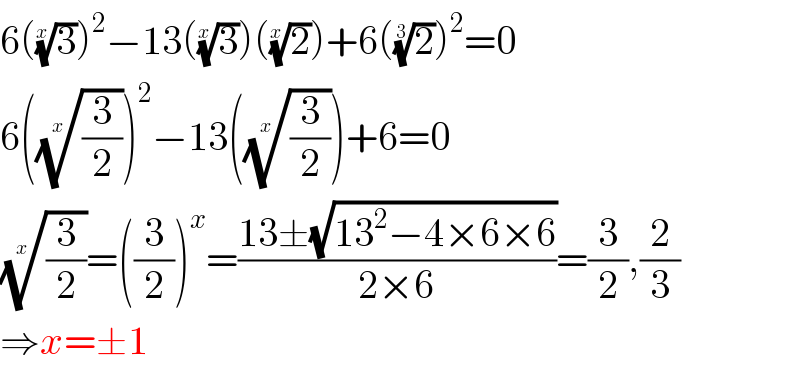
$$\mathrm{6}\left(\sqrt[{{x}}]{\mathrm{3}}\right)^{\mathrm{2}} −\mathrm{13}\left(\sqrt[{{x}}]{\mathrm{3}}\right)\left(\sqrt[{{x}}]{\mathrm{2}}\right)+\mathrm{6}\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{6}\left(\sqrt[{{x}}]{\frac{\mathrm{3}}{\mathrm{2}}}\right)^{\mathrm{2}} −\mathrm{13}\left(\sqrt[{{x}}]{\frac{\mathrm{3}}{\mathrm{2}}}\right)+\mathrm{6}=\mathrm{0} \\ $$$$\sqrt[{{x}}]{\frac{\mathrm{3}}{\mathrm{2}}}=\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{{x}} =\frac{\mathrm{13}\pm\sqrt{\mathrm{13}^{\mathrm{2}} −\mathrm{4}×\mathrm{6}×\mathrm{6}}}{\mathrm{2}×\mathrm{6}}=\frac{\mathrm{3}}{\mathrm{2}},\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow{x}=\pm\mathrm{1} \\ $$
