Question Number 104411 by ajfour last updated on 21/Jul/20

Commented by ajfour last updated on 21/Jul/20
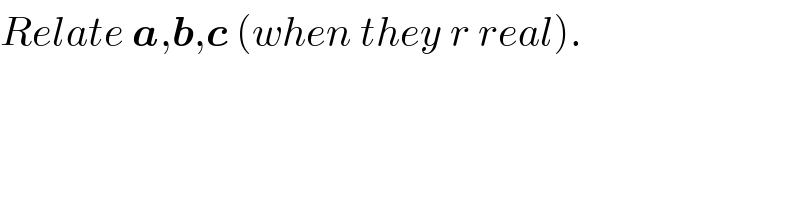
$${Relate}\:\boldsymbol{{a}},\boldsymbol{{b}},\boldsymbol{{c}}\:\left({when}\:{they}\:{r}\:{real}\right). \\ $$
Commented by mr W last updated on 21/Jul/20
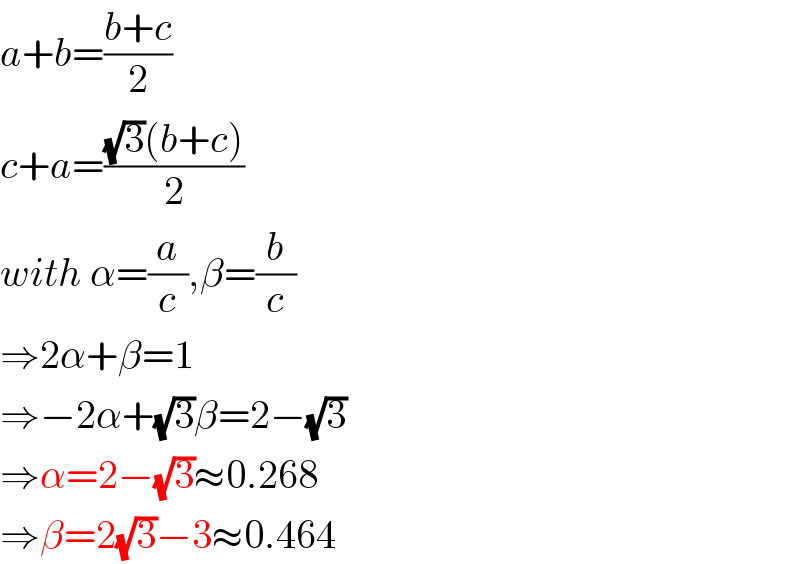
$${a}+{b}=\frac{{b}+{c}}{\mathrm{2}} \\ $$$${c}+{a}=\frac{\sqrt{\mathrm{3}}\left({b}+{c}\right)}{\mathrm{2}} \\ $$$${with}\:\alpha=\frac{{a}}{{c}},\beta=\frac{{b}}{{c}} \\ $$$$\Rightarrow\mathrm{2}\alpha+\beta=\mathrm{1} \\ $$$$\Rightarrow−\mathrm{2}\alpha+\sqrt{\mathrm{3}}\beta=\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\alpha=\mathrm{2}−\sqrt{\mathrm{3}}\approx\mathrm{0}.\mathrm{268} \\ $$$$\Rightarrow\beta=\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{3}\approx\mathrm{0}.\mathrm{464} \\ $$
Commented by ajfour last updated on 21/Jul/20

$${It}\:{isn}'{t}\:{like}\:{that}\:{Sir}… \\ $$$${please}\:{view}\:{Q}.\mathrm{104445} \\ $$
Commented by mr W last updated on 21/Jul/20
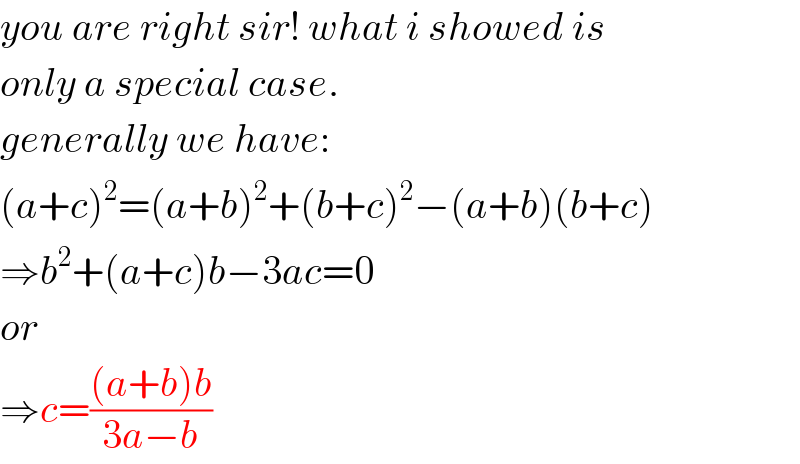
$${you}\:{are}\:{right}\:{sir}!\:{what}\:{i}\:{showed}\:{is} \\ $$$${only}\:{a}\:{special}\:{case}. \\ $$$${generally}\:{we}\:{have}: \\ $$$$\left({a}+{c}\right)^{\mathrm{2}} =\left({a}+{b}\right)^{\mathrm{2}} +\left({b}+{c}\right)^{\mathrm{2}} −\left({a}+{b}\right)\left({b}+{c}\right) \\ $$$$\Rightarrow{b}^{\mathrm{2}} +\left({a}+{c}\right){b}−\mathrm{3}{ac}=\mathrm{0} \\ $$$${or} \\ $$$$\Rightarrow{c}=\frac{\left({a}+{b}\right){b}}{\mathrm{3}{a}−{b}} \\ $$
Commented by ajfour last updated on 21/Jul/20

$${Excellent}\:{and}\:{very}\:{pragmatic}\:{notice} \\ $$$${Sir},\:{i}\:{follow}\:{it}\:{well},\:{thanks}\:{a}\:{lot}. \\ $$
