Question-104468

Question Number 104468 by ajfour last updated on 21/Jul/20

Commented by ajfour last updated on 21/Jul/20

Find r and hence area of △ABC in terms of R.

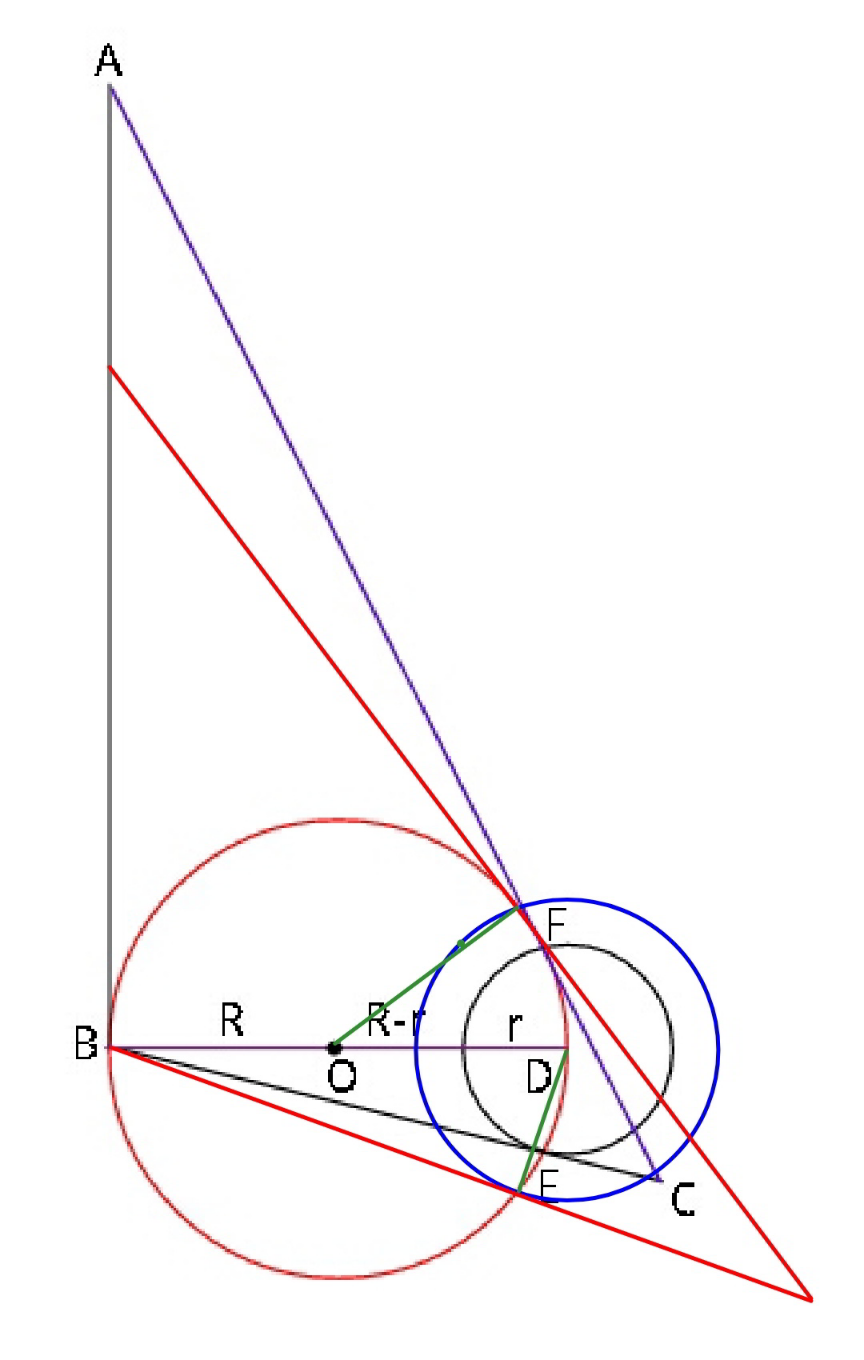
$${Find}\:{r}\:{and}\:{hence}\:{area}\:{of}\:\bigtriangleup{ABC}\:{in} \\ $$$${terms}\:{of}\:{R}. \\ $$

Commented by mr W last updated on 22/Jul/20

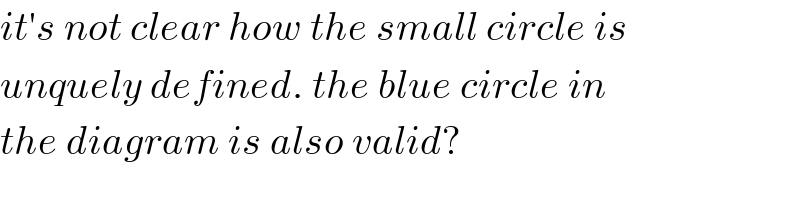
$${it}'{s}\:{not}\:{clear}\:{how}\:{the}\:{small}\:{circle}\:{is} \\ $$$${unquely}\:{defined}.\:{the}\:{blue}\:{circle}\:{in} \\ $$$${the}\:{diagram}\:{is}\:{also}\:{valid}? \\ $$

Commented by mr W last updated on 22/Jul/20

Commented by malwaan last updated on 22/Jul/20

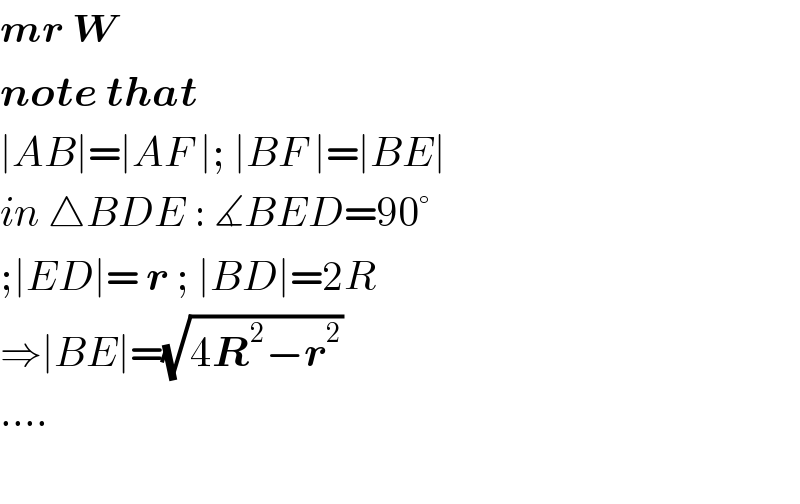
mr W note that ∣AB∣=∣AF ∣; ∣BF ∣=∣BE∣ in △BDE : ∡BED=90° ;∣ED∣= r ; ∣BD∣=2R ⇒∣BE∣=(√(4R^2 −r^2 )) ....

$$\boldsymbol{{mr}}\:\boldsymbol{{W}} \\ $$$$\boldsymbol{{note}}\:\boldsymbol{{that}} \\ $$$$\mid{AB}\mid=\mid{AF}\:\mid;\:\mid{BF}\:\mid=\mid{BE}\mid \\ $$$${in}\:\bigtriangleup{BDE}\::\:\measuredangle{BED}=\mathrm{90}° \\ $$$$;\mid{ED}\mid=\:\boldsymbol{{r}}\:;\:\mid{BD}\mid=\mathrm{2}{R} \\ $$$$\Rightarrow\mid{BE}\mid=\sqrt{\mathrm{4}\boldsymbol{{R}}^{\mathrm{2}} −\boldsymbol{{r}}^{\mathrm{2}} } \\ $$$$…. \\ $$$$ \\ $$

Commented by mr W last updated on 22/Jul/20

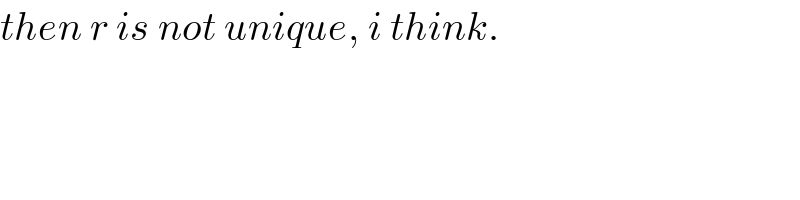
$${then}\:{r}\:{is}\:{not}\:{unique},\:{i}\:{think}. \\ $$

Commented by ajfour last updated on 22/Jul/20

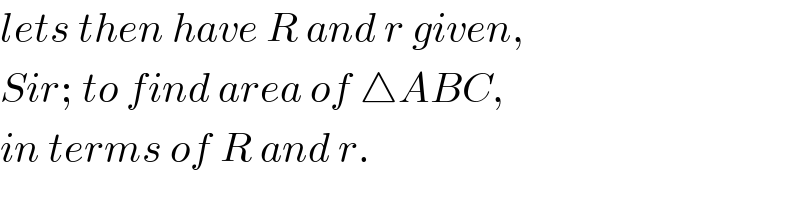
lets then have R and r given, Sir; to find area of △ABC, in terms of R and r.

$${lets}\:{then}\:{have}\:{R}\:{and}\:{r}\:{given}, \\ $$$${Sir};\:{to}\:{find}\:{area}\:{of}\:\bigtriangleup{ABC}, \\ $$$${in}\:{terms}\:{of}\:{R}\:{and}\:{r}. \\ $$

Commented by malwaan last updated on 22/Jul/20

it depend on the location of the point A SO you are absolutely right mr W

$${it}\:{depend}\:{on}\:{the}\:{location} \\ $$$${of}\:{the}\:{point}\:\boldsymbol{{A}} \\ $$$$\boldsymbol{{SO}}\:{you}\:{are}\:{absolutely}\:{right} \\ $$$${mr}\:{W} \\ $$

Answered by mr W last updated on 22/Jul/20

Commented by mr W last updated on 22/Jul/20

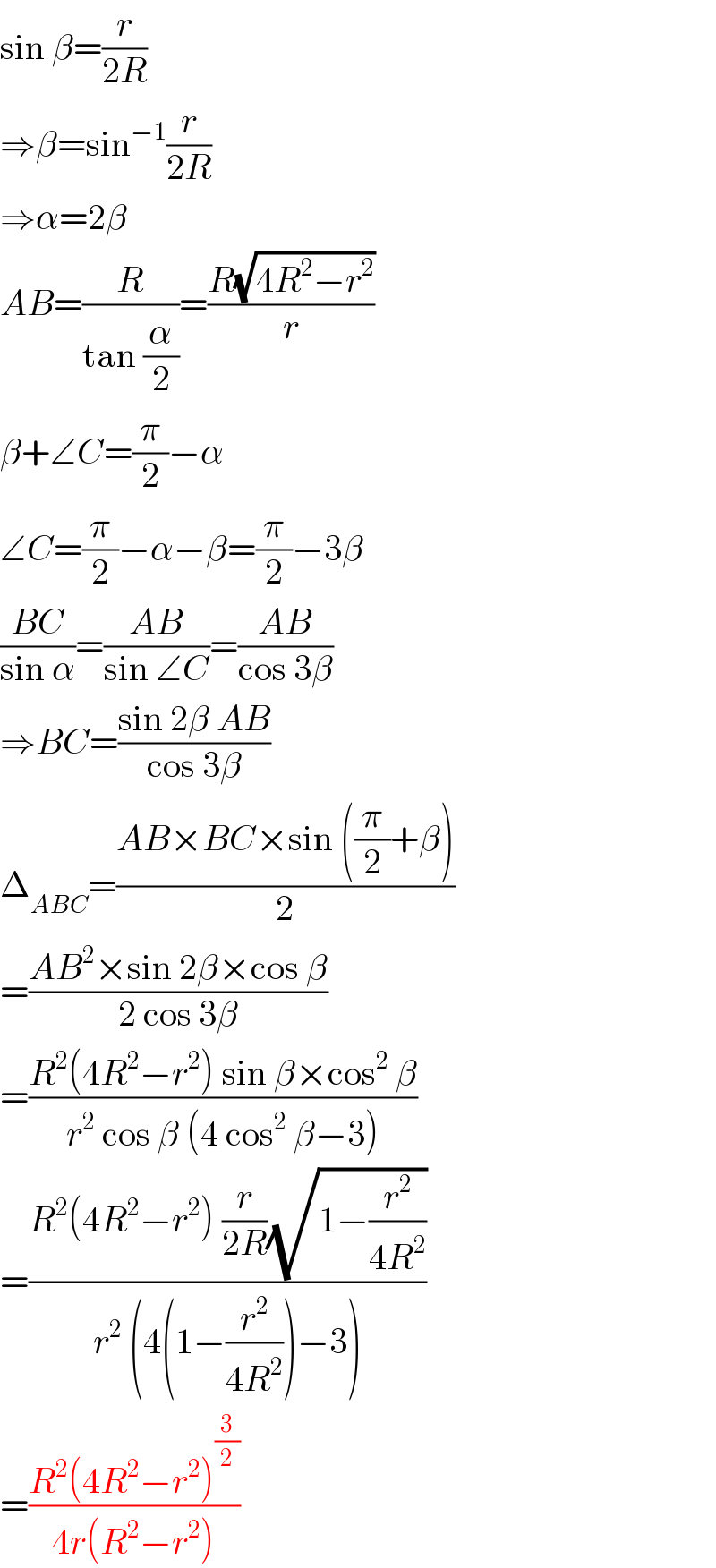
sin β=(r/(2R)) ⇒β=sin^(−1) (r/(2R)) ⇒α=2β AB=(R/(tan (α/2)))=((R(√(4R^2 −r^2 )))/r) β+∠C=(π/2)−α ∠C=(π/2)−α−β=(π/2)−3β ((BC)/(sin α))=((AB)/(sin ∠C))=((AB)/(cos 3β)) ⇒BC=((sin 2β AB)/(cos 3β)) Δ_(ABC) =((AB×BC×sin ((π/2)+β))/2) =((AB^2 ×sin 2β×cos β)/(2 cos 3β)) =((R^2 (4R^2 −r^2 ) sin β×cos^2 β)/(r^2 cos β (4 cos^2 β−3))) =((R^2 (4R^2 −r^2 ) (r/(2R))(√(1−(r^2 /(4R^2 )))))/(r^2 (4(1−(r^2 /(4R^2 )))−3))) =((R^2 (4R^2 −r^2 )^(3/2) )/(4r(R^2 −r^2 )))

$$\mathrm{sin}\:\beta=\frac{{r}}{\mathrm{2}{R}} \\ $$$$\Rightarrow\beta=\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{\mathrm{2}{R}} \\ $$$$\Rightarrow\alpha=\mathrm{2}\beta \\ $$$${AB}=\frac{{R}}{\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}}=\frac{{R}\sqrt{\mathrm{4}{R}^{\mathrm{2}} −{r}^{\mathrm{2}} }}{{r}} \\ $$$$\beta+\angle{C}=\frac{\pi}{\mathrm{2}}−\alpha \\ $$$$\angle{C}=\frac{\pi}{\mathrm{2}}−\alpha−\beta=\frac{\pi}{\mathrm{2}}−\mathrm{3}\beta \\ $$$$\frac{{BC}}{\mathrm{sin}\:\alpha}=\frac{{AB}}{\mathrm{sin}\:\angle{C}}=\frac{{AB}}{\mathrm{cos}\:\mathrm{3}\beta} \\ $$$$\Rightarrow{BC}=\frac{\mathrm{sin}\:\mathrm{2}\beta\:{AB}}{\mathrm{cos}\:\mathrm{3}\beta} \\ $$$$\Delta_{{ABC}} =\frac{{AB}×{BC}×\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}+\beta\right)}{\mathrm{2}} \\ $$$$=\frac{{AB}^{\mathrm{2}} ×\mathrm{sin}\:\mathrm{2}\beta×\mathrm{cos}\:\beta}{\mathrm{2}\:\mathrm{cos}\:\mathrm{3}\beta} \\ $$$$=\frac{{R}^{\mathrm{2}} \left(\mathrm{4}{R}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)\:\mathrm{sin}\:\beta×\mathrm{cos}^{\mathrm{2}} \:\beta}{{r}^{\mathrm{2}} \:\mathrm{cos}\:\beta\:\left(\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\beta−\mathrm{3}\right)} \\ $$$$=\frac{{R}^{\mathrm{2}} \left(\mathrm{4}{R}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)\:\frac{{r}}{\mathrm{2}{R}}\sqrt{\mathrm{1}−\frac{{r}^{\mathrm{2}} }{\mathrm{4}{R}^{\mathrm{2}} }}}{{r}^{\mathrm{2}} \:\left(\mathrm{4}\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{\mathrm{4}{R}^{\mathrm{2}} }\right)−\mathrm{3}\right)} \\ $$$$=\frac{{R}^{\mathrm{2}} \left(\mathrm{4}{R}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{4}{r}\left({R}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)} \\ $$

Commented by ajfour last updated on 24/Jul/20

$${thanks}\:{sir},\:{shall}\:{review}\:{it},\:{bit} \\ $$$${unwell}\:{again}.. \\ $$$${Elegant}\:{Solving}\:{Sir},\:{too}\:{good}\:{to} \\ $$$${follow}\:{it}\:{even},\:{thanks}\:{a}\:{lot}! \\ $$

Commented by mr W last updated on 23/Jul/20

$${get}\:{well}! \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply