Question Number 104517 by Quvonchbek last updated on 22/Jul/20

Answered by 1549442205PVT last updated on 22/Jul/20

$$\mathrm{It}\:\mathrm{is}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{see}\:\mathrm{that}\:\mathrm{the}\:\mathrm{sequence}\:\mathrm{of}\:\mathrm{numbers}: \\ $$$$\mathrm{11},\mathrm{19},\mathrm{29},\mathrm{41},…\mathrm{has}\:\mathrm{general}\:\mathrm{term}\:\mathrm{is} \\ $$$$\mathrm{n}^{\mathrm{2}} +\mathrm{3n}+\mathrm{1}\left(\mathrm{n}\in\mathbb{N}^{\ast} \right).\mathrm{Hence}, \\ $$$$\mathrm{S}=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\Sigma}}\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{3n}+\mathrm{1}}{\mathrm{n}!}=\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\Sigma}}\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{n}!}+\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\Sigma}}\frac{\mathrm{3n}}{\mathrm{n}!}+\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\Sigma}}\frac{\mathrm{1}}{\mathrm{n}!}\left(\ast\right) \\ $$$$\mathrm{On}\:\mathrm{the}\:\mathrm{other}\:\mathrm{hands},\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{e}=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\Sigma}}\frac{\mathrm{1}}{\mathrm{n}!}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{4}!}+…\mathrm{Hence}, \\ $$$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{3n}}{\mathrm{n}!}=\frac{\mathrm{3}}{\mathrm{1}!}+\frac{\mathrm{3}.\mathrm{2}}{\mathrm{2}!}+\frac{\mathrm{3}.\mathrm{3}}{\mathrm{3}!}+\frac{\mathrm{3}.\mathrm{4}}{\mathrm{4}!}+… \\ $$$$=\mathrm{3}+\frac{\mathrm{3}}{\mathrm{1}!}+\frac{\mathrm{3}}{\mathrm{2}!}+\frac{\mathrm{3}}{\mathrm{3}!}+…=\mathrm{3}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+…\right) \\ $$$$=\mathrm{3e}\left(\mathrm{1}\right).\mathrm{Also}\:\mathrm{we}\:\mathrm{have}\:\mathrm{also} \\ $$$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}!}=\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+…=\mathrm{e}−\mathrm{1}\left(\mathrm{1}\right) \\ $$$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{n}!}=\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{4}}{\mathrm{2}!}+\frac{\mathrm{9}}{\mathrm{3}!}+\frac{\mathrm{16}}{\mathrm{4}!}+… \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{2}}{\mathrm{1}!}+\frac{\mathrm{3}}{\mathrm{2}!}+\frac{\mathrm{4}}{\mathrm{3}!}+… \\ $$$$\mathrm{We}\:\mathrm{have}\:\mathrm{also}\:\mathrm{that} \\ $$$$\mathrm{e}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{4}!}+… \\ $$$$=\mathrm{1}+\frac{\mathrm{2}−\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{3}−\mathrm{2}}{\mathrm{2}!}+\frac{\mathrm{4}−\mathrm{3}}{\mathrm{3}!}+\frac{\mathrm{5}−\mathrm{4}}{\mathrm{4}!}+… \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{2}}{\mathrm{1}!}+\frac{\mathrm{3}}{\mathrm{2}!}+\frac{\mathrm{4}}{\mathrm{3}!}+\frac{\mathrm{5}}{\mathrm{4}!}+…−\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+…\right) \\ $$$$=\mathrm{1}+\frac{\mathrm{2}}{\mathrm{1}!}+\frac{\mathrm{3}}{\mathrm{2}!}+\frac{\mathrm{4}}{\mathrm{3}!}+\frac{\mathrm{5}}{\mathrm{4}!}+…−\mathrm{e} \\ $$$$\Rightarrow\mathrm{2e}=\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{2}}{\mathrm{1}!}+\frac{\mathrm{3}}{\mathrm{2}!}+\frac{\mathrm{4}}{\mathrm{3}!}+\frac{\mathrm{5}}{\mathrm{4}!}+…\left(\mathrm{2}\right) \\ $$$$\mathrm{From}\left(\ast\right),\:\left(\mathrm{1}\right)\mathrm{and}\left(\mathrm{2}\right)\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{S}=\Sigma\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{3n}+\mathrm{1}}{\mathrm{n}!}=\mathrm{e}−\mathrm{1}+\mathrm{3e}+\mathrm{2e}=\mathrm{6e}−\mathrm{1} \\ $$$$=\mathrm{ae}^{\mathrm{b}} +\mathrm{c}\Rightarrow\mathrm{a}=\mathrm{6},\mathrm{b}=\mathrm{1},\mathrm{c}=−\mathrm{1}.\mathrm{Therefore}, \\ $$$$\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{c}}=\mathrm{6} \\ $$
Commented by OlafThorendsen last updated on 22/Jul/20

$$\mathrm{The}\:\mathrm{sum}\:\mathrm{starts}\:\mathrm{at}\:\mathrm{1},\:\mathrm{not}\:\mathrm{at}\:\mathrm{0}. \\ $$$$\mathrm{Finally}\:\mathrm{the}\:\mathrm{good}\:\mathrm{result}\:\mathrm{is}\:\mathrm{6e}−\mathrm{1}\:\mathrm{sir}. \\ $$
Commented by 1549442205PVT last updated on 22/Jul/20

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}.\mathrm{I}\:\mathrm{mistaked}\:\mathrm{and} \\ $$$$\mathrm{corrected}. \\ $$
Answered by OlafThorendsen last updated on 22/Jul/20
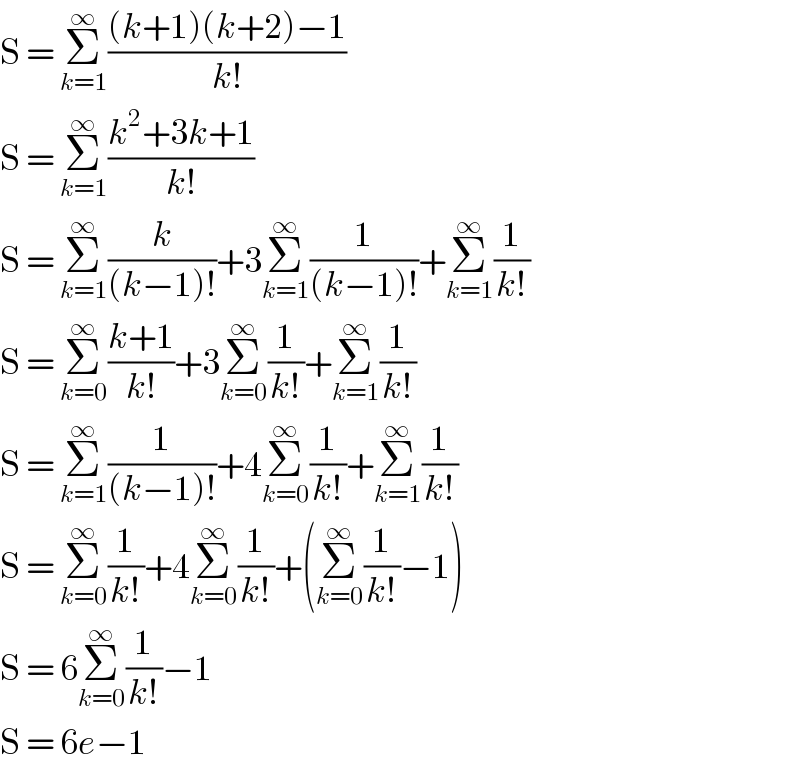
$$\mathrm{S}\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)−\mathrm{1}}{{k}!} \\ $$$$\mathrm{S}\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{k}^{\mathrm{2}} +\mathrm{3}{k}+\mathrm{1}}{{k}!} \\ $$$$\mathrm{S}\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{k}}{\left({k}−\mathrm{1}\right)!}+\mathrm{3}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({k}−\mathrm{1}\right)!}+\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}!} \\ $$$$\mathrm{S}\:=\:\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{k}+\mathrm{1}}{{k}!}+\mathrm{3}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}!}+\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}!} \\ $$$$\mathrm{S}\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({k}−\mathrm{1}\right)!}+\mathrm{4}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}!}+\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}!} \\ $$$$\mathrm{S}\:=\:\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}!}+\mathrm{4}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}!}+\left(\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}!}−\mathrm{1}\right) \\ $$$$\mathrm{S}\:=\:\mathrm{6}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}!}−\mathrm{1} \\ $$$$\mathrm{S}\:=\:\mathrm{6}{e}−\mathrm{1} \\ $$
Commented by Dwaipayan Shikari last updated on 22/Jul/20
��
Commented by Dwaipayan Shikari last updated on 22/Jul/20

$${Great}\:{solution} \\ $$
Commented by mr W last updated on 22/Jul/20

$${i}\:{agree}\:{with}\:{MJS}\:{sir}.\:{in}\:{fact}\:{the} \\ $$$${sum}\:{of}\:{LHS}\:{is}\:{not}\:{unique},\:{since}\:{the} \\ $$$${a}_{{n}} \:{term}\:{is}\:{not}\:{defined}! \\ $$
Commented by 1549442205PVT last updated on 22/Jul/20

$$\mathrm{we}\:\mathrm{can}\:\mathrm{find}\:\mathrm{out}\:\mathrm{the}\:\mathrm{rule}\:\mathrm{to}\:\mathrm{define}\: \\ $$$$\mathrm{general}\:\mathrm{term}\:\mathrm{follows}\:\mathrm{as}: \\ $$$$\mathrm{a}_{\mathrm{1}} =\mathrm{5},\mathrm{a}_{\mathrm{2}} =\mathrm{11},\mathrm{a}_{\mathrm{3}} =\mathrm{19},\mathrm{a}_{\mathrm{4}} =\mathrm{29},\mathrm{a}_{\mathrm{5}} =\mathrm{41}.\mathrm{So}, \\ $$$$\begin{vmatrix}{\mathrm{a}_{\mathrm{2}} −\mathrm{a}_{\mathrm{1}} }&{\mathrm{a}_{\mathrm{3}} −\mathrm{a}_{\mathrm{2}} }&{\mathrm{a}_{\mathrm{4}} −\mathrm{a}_{\mathrm{3}} }&{\mathrm{a}_{\mathrm{5}} −\mathrm{a}_{\mathrm{4}} }\\{\mathrm{6}}&{\mathrm{8}}&{\mathrm{10}}&{\mathrm{12}}\end{vmatrix} \\ $$$$\mathrm{Since}\:\mathrm{12}−\mathrm{10}=\mathrm{10}−\mathrm{8}=\mathrm{8}−\mathrm{6}\:,\mathrm{it}\:\mathrm{follows} \\ $$$$\mathrm{that}\:\mathrm{the}\:\mathrm{sequence}\:\mathrm{6},\mathrm{8},\mathrm{10},\mathrm{12}\:…\mathrm{form} \\ $$$$\mathrm{an}\:\mathrm{arithmetic}\:\mathrm{progression}\:\mathrm{which}\:\mathrm{has} \\ $$$$\mathrm{the}\:\mathrm{difference}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{2}.\mathrm{Hence}\:\mathrm{its} \\ $$$$\mathrm{general}\:\mathrm{term}\:\mathrm{is}\:\mathrm{2n}+\mathrm{4}.\mathrm{So},\mathrm{by}\:\mathrm{above}\:\mathrm{result} \\ $$$$\mathrm{a}_{\mathrm{n}+\mathrm{1}} −\mathrm{a}_{\mathrm{n}} =\mathrm{2n}+\mathrm{4}.\mathrm{It}\:\mathrm{follows}\:\mathrm{that} \\ $$$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\mathrm{a}_{\mathrm{k}+\mathrm{1}} −\mathrm{a}_{\mathrm{k}} \right)=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\Sigma}}\left(\mathrm{2k}+\mathrm{4}\right) \\ $$$$\Rightarrow\mathrm{a}_{\mathrm{n}+\mathrm{1}} −\mathrm{a}_{\mathrm{1}} =\mathrm{2}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\Sigma}}\mathrm{k}+\mathrm{4n}=\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)+\mathrm{4n} \\ $$$$\Rightarrow\boldsymbol{\mathrm{a}}_{\boldsymbol{\mathrm{n}}+\mathrm{1}} =\boldsymbol{\mathrm{n}}^{\mathrm{2}} +\mathrm{5}\boldsymbol{\mathrm{n}}+\mathrm{5}\Rightarrow\boldsymbol{\mathrm{a}}_{\boldsymbol{\mathrm{n}}} =\boldsymbol{\mathrm{n}}^{\mathrm{2}} +\mathrm{3}\boldsymbol{\mathrm{n}}+\mathrm{1} \\ $$$$ \\ $$
