Question-104696

Question Number 104696 by nimnim last updated on 23/Jul/20

Answered by Rasheed.Sindhi last updated on 23/Jul/20

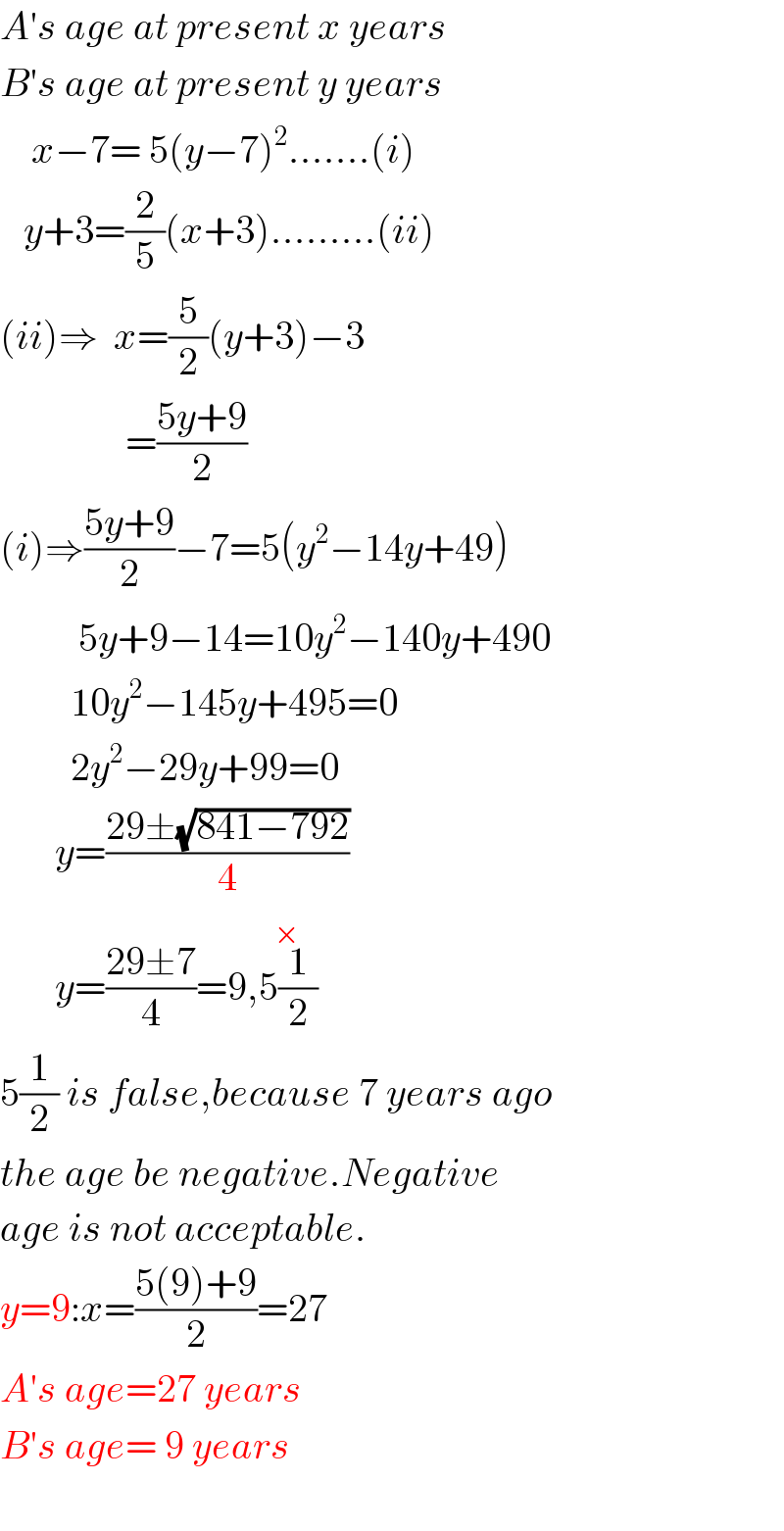
A′s age at present x years B′s age at present y years x−7= 5(y−7)^2 .......(i) y+3=(2/5)(x+3).........(ii) (ii)⇒ x=(5/2)(y+3)−3 =((5y+9)/2) (i)⇒((5y+9)/2)−7=5(y^2 −14y+49) 5y+9−14=10y^2 −140y+490 10y^2 −145y+495=0 2y^2 −29y+99=0 y=((29±(√(841−792)))/4) y=((29±7)/4)=9,5(1/2)^(×) 5(1/2) is false,because 7 years ago the age be negative.Negative age is not acceptable. y=9:x=((5(9)+9)/2)=27 A′s age=27 years B′s age= 9 years

$${A}'{s}\:{age}\:{at}\:{present}\:{x}\:{years} \\ $$$${B}'{s}\:{age}\:{at}\:{present}\:{y}\:{years} \\ $$$$\:\:\:\:{x}−\mathrm{7}=\:\mathrm{5}\left({y}−\mathrm{7}\right)^{\mathrm{2}} …….\left({i}\right) \\ $$$$\:\:\:{y}+\mathrm{3}=\frac{\mathrm{2}}{\mathrm{5}}\left({x}+\mathrm{3}\right)………\left({ii}\right) \\ $$$$\left({ii}\right)\Rightarrow\:\:{x}=\frac{\mathrm{5}}{\mathrm{2}}\left({y}+\mathrm{3}\right)−\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{5}{y}+\mathrm{9}}{\mathrm{2}} \\ $$$$\left({i}\right)\Rightarrow\frac{\mathrm{5}{y}+\mathrm{9}}{\mathrm{2}}−\mathrm{7}=\mathrm{5}\left({y}^{\mathrm{2}} −\mathrm{14}{y}+\mathrm{49}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{5}{y}+\mathrm{9}−\mathrm{14}=\mathrm{10}{y}^{\mathrm{2}} −\mathrm{140}{y}+\mathrm{490} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{10}{y}^{\mathrm{2}} −\mathrm{145}{y}+\mathrm{495}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{2}{y}^{\mathrm{2}} −\mathrm{29}{y}+\mathrm{99}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:{y}=\frac{\mathrm{29}\pm\sqrt{\mathrm{841}−\mathrm{792}}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:{y}=\frac{\mathrm{29}\pm\mathrm{7}}{\mathrm{4}}=\mathrm{9},\overset{×} {\mathrm{5}\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{5}\frac{\mathrm{1}}{\mathrm{2}}\:{is}\:{false},{because}\:\mathrm{7}\:{years}\:{ago} \\ $$$${the}\:{age}\:{be}\:{negative}.{Negative} \\ $$$${age}\:{is}\:{not}\:{acceptable}. \\ $$$${y}=\mathrm{9}:{x}=\frac{\mathrm{5}\left(\mathrm{9}\right)+\mathrm{9}}{\mathrm{2}}=\mathrm{27} \\ $$$${A}'{s}\:{age}=\mathrm{27}\:{years} \\ $$$${B}'{s}\:{age}=\:\mathrm{9}\:{years} \\ $$$$ \\ $$

Commented by 1549442205PVT last updated on 23/Jul/20

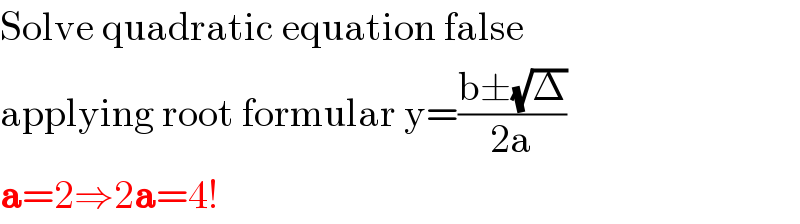
Solve quadratic equation false applying root formular y=((b±(√Δ))/(2a)) a=2⇒2a=4!

$$\mathrm{Solve}\:\mathrm{quadratic}\:\mathrm{equation}\:\mathrm{false} \\ $$$$\mathrm{applying}\:\mathrm{root}\:\mathrm{formular}\:\mathrm{y}=\frac{\mathrm{b}\pm\sqrt{\Delta}}{\mathrm{2a}} \\ $$$$\boldsymbol{\mathrm{a}}=\mathrm{2}\Rightarrow\mathrm{2}\boldsymbol{\mathrm{a}}=\mathrm{4}! \\ $$

Commented by Rasheed.Sindhi last updated on 23/Jul/20

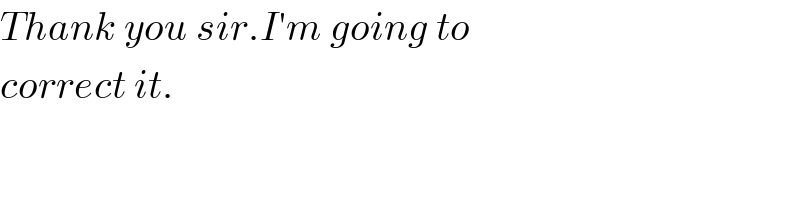
$${Thank}\:{you}\:{sir}.{I}'{m}\:{going}\:{to} \\ $$$${correct}\:{it}. \\ $$

Commented by nimnim last updated on 23/Jul/20

$${Thank}\:{you}\:{Sir}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply