Question-104701

Question Number 104701 by abony1303 last updated on 23/Jul/20

Commented by abony1303 last updated on 23/Jul/20

$$\mathrm{Pls}\:\mathrm{help} \\ $$

Answered by mathmax by abdo last updated on 23/Jul/20

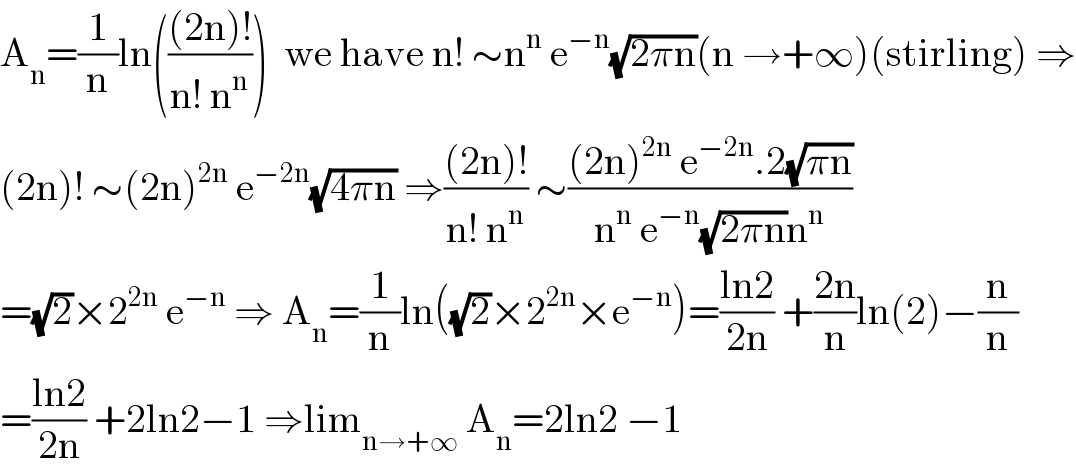
A_n =(1/n)ln((((2n)!)/(n! n^n ))) we have n! ∼n^n e^(−n) (√(2πn))(n →+∞)(stirling) ⇒ (2n)! ∼(2n)^(2n) e^(−2n) (√(4πn)) ⇒(((2n)!)/(n! n^n )) ∼(((2n)^(2n) e^(−2n) .2(√(πn)))/(n^n e^(−n) (√(2πn))n^n )) =(√2)×2^(2n) e^(−n) ⇒ A_n =(1/n)ln((√2)×2^(2n) ×e^(−n) )=((ln2)/(2n)) +((2n)/n)ln(2)−(n/n) =((ln2)/(2n)) +2ln2−1 ⇒lim_(n→+∞) A_n =2ln2 −1

$$\mathrm{A}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{n}}\mathrm{ln}\left(\frac{\left(\mathrm{2n}\right)!}{\mathrm{n}!\:\mathrm{n}^{\mathrm{n}} }\right)\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{n}!\:\sim\mathrm{n}^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{n}} \sqrt{\mathrm{2}\pi\mathrm{n}}\left(\mathrm{n}\:\rightarrow+\infty\right)\left(\mathrm{stirling}\right)\:\Rightarrow \\ $$$$\left(\mathrm{2n}\right)!\:\sim\left(\mathrm{2n}\right)^{\mathrm{2n}} \:\mathrm{e}^{−\mathrm{2n}} \sqrt{\mathrm{4}\pi\mathrm{n}}\:\Rightarrow\frac{\left(\mathrm{2n}\right)!}{\mathrm{n}!\:\mathrm{n}^{\mathrm{n}} }\:\sim\frac{\left(\mathrm{2n}\right)^{\mathrm{2n}} \:\mathrm{e}^{−\mathrm{2n}} .\mathrm{2}\sqrt{\pi\mathrm{n}}}{\mathrm{n}^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{n}} \sqrt{\mathrm{2}\pi\mathrm{n}}\mathrm{n}^{\mathrm{n}} } \\ $$$$=\sqrt{\mathrm{2}}×\mathrm{2}^{\mathrm{2n}} \:\mathrm{e}^{−\mathrm{n}} \:\Rightarrow\:\mathrm{A}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{n}}\mathrm{ln}\left(\sqrt{\mathrm{2}}×\mathrm{2}^{\mathrm{2n}} ×\mathrm{e}^{−\mathrm{n}} \right)=\frac{\mathrm{ln2}}{\mathrm{2n}}\:+\frac{\mathrm{2n}}{\mathrm{n}}\mathrm{ln}\left(\mathrm{2}\right)−\frac{\mathrm{n}}{\mathrm{n}} \\ $$$$=\frac{\mathrm{ln2}}{\mathrm{2n}}\:+\mathrm{2ln2}−\mathrm{1}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{A}_{\mathrm{n}} =\mathrm{2ln2}\:−\mathrm{1} \\ $$

Commented by abony1303 last updated on 23/Jul/20

$$\mathrm{couldnt}\:\mathrm{catch}\:\mathrm{you}\:\mathrm{ser}\::\left(\right. \\ $$

Commented by mathmax by abdo last updated on 23/Jul/20

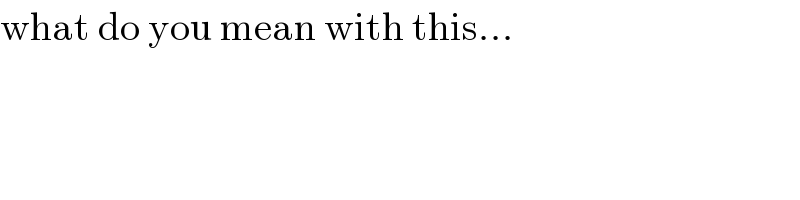
$$\mathrm{what}\:\mathrm{do}\:\mathrm{you}\:\mathrm{mean}\:\mathrm{with}\:\mathrm{this}… \\ $$

Commented by abony1303 last updated on 23/Jul/20

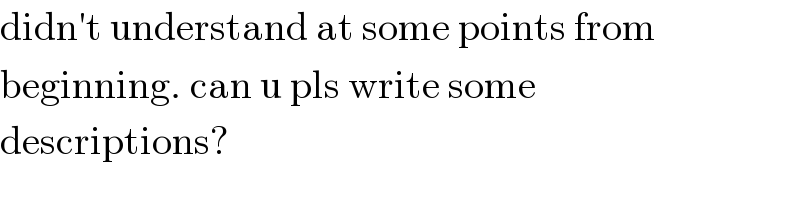
didn′t understand at some points from beginning. can u pls write some descriptions?

$$\mathrm{didn}'\mathrm{t}\:\mathrm{understand}\:\mathrm{at}\:\mathrm{some}\:\mathrm{points}\:\mathrm{from} \\ $$$$\mathrm{beginning}.\:\mathrm{can}\:\mathrm{u}\:\mathrm{pls}\:\mathrm{write}\:\mathrm{some} \\ $$$$\mathrm{descriptions}? \\ $$

Commented by abony1303 last updated on 24/Jul/20

Thank you ser. It was very helpful. Didnt′t know about Sterling′s approximation.

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{ser}.\:\mathrm{It}\:\mathrm{was}\:\mathrm{very}\:\mathrm{helpful}. \\ $$$$\mathrm{Didnt}'\mathrm{t}\:\mathrm{know}\:\mathrm{about}\:\mathrm{Sterling}'\mathrm{s} \\ $$$$\mathrm{approximation}. \\ $$

Commented by mathmax by abdo last updated on 24/Jul/20

here i have used th stirling formula n! ∼ n^n e^(−n) (√(2πn)) (for n →+∞) i think the answer is clear

$$\mathrm{here}\:\mathrm{i}\:\mathrm{have}\:\mathrm{used}\:\mathrm{th}\:\mathrm{stirling}\:\mathrm{formula}\:\:\mathrm{n}!\:\sim\:\mathrm{n}^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{n}} \sqrt{\mathrm{2}\pi\mathrm{n}}\:\:\left(\mathrm{for}\:\mathrm{n}\:\rightarrow+\infty\right) \\ $$$$\:\mathrm{i}\:\mathrm{think}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{clear}\: \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply