Question Number 104703 by abony1303 last updated on 23/Jul/20

Commented by abony1303 last updated on 23/Jul/20

$$\left.\mathrm{pls}\:\mathrm{help}\:\mathrm{too}\::\right) \\ $$
Answered by bemath last updated on 23/Jul/20
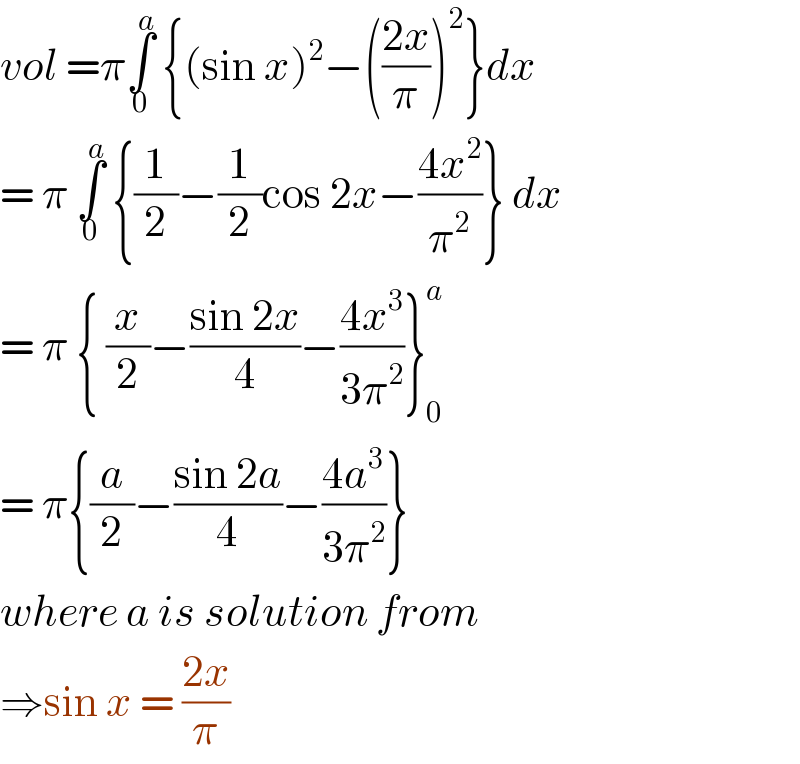
$${vol}\:=\pi\underset{\mathrm{0}} {\overset{{a}} {\int}}\:\left\{\left(\mathrm{sin}\:{x}\right)^{\mathrm{2}} −\left(\frac{\mathrm{2}{x}}{\pi}\right)^{\mathrm{2}} \right\}{dx} \\ $$$$=\:\pi\:\underset{\mathrm{0}} {\overset{{a}} {\int}}\:\left\{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}{x}−\frac{\mathrm{4}{x}^{\mathrm{2}} }{\pi^{\mathrm{2}} }\right\}\:{dx} \\ $$$$=\:\pi\:\left\{\:\frac{{x}}{\mathrm{2}}−\frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{4}}−\frac{\mathrm{4}{x}^{\mathrm{3}} }{\mathrm{3}\pi^{\mathrm{2}} }\right\}_{\mathrm{0}} ^{{a}} \\ $$$$=\:\pi\left\{\frac{{a}}{\mathrm{2}}−\frac{\mathrm{sin}\:\mathrm{2}{a}}{\mathrm{4}}−\frac{\mathrm{4}{a}^{\mathrm{3}} }{\mathrm{3}\pi^{\mathrm{2}} }\right\} \\ $$$${where}\:{a}\:{is}\:{solution}\:{from} \\ $$$$\Rightarrow\mathrm{sin}\:{x}\:=\:\frac{\mathrm{2}{x}}{\pi} \\ $$
