Question-104735

Question Number 104735 by bemath last updated on 23/Jul/20

Commented by 1549442205PVT last updated on 23/Jul/20

$$\boldsymbol{\mathrm{what}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{your}}\:\boldsymbol{\mathrm{question}}? \\ $$

Commented by bemath last updated on 23/Jul/20

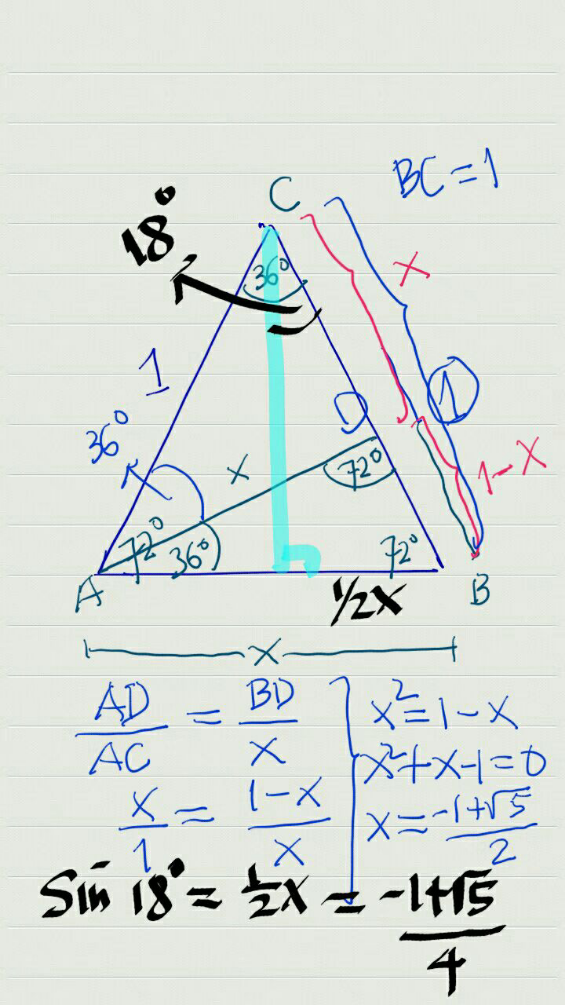
find the value of sin 18° in geometrically

$${find}\:{the}\:{value}\:{of}\:\mathrm{sin}\:\mathrm{18}°\:{in} \\ $$$${geometrically} \\ $$

Answered by 1549442205PVT last updated on 24/Jul/20

Commented by 1549442205PVT last updated on 24/Jul/20

Drawing an isosceles triamgle ABC,CA=CB=a with ACB^(�) =36°.Then CAB^(�) =CBA^(�) =72°. A point D taken on the side BC such that DA=DC=m.Denote the midpoont of side AB by E.Then we get DCA^(�) =DAC^(�) =36° ⇒DAB^(�) =72°−36°=36°⇒ADB^(�) =72°,so ΔABD is isosceles at A⇒AB=AD=m and hence ΔABD⋍ΔCAB(a.a) ⇒((AD)/(BC))=((BD)/(AB))⇔(m/a)=((a−m)/m)⇔a^2 −am−m^2 =0 This is a quadratic equation for a with (√Δ)=(√(m^2 +4m^2 ))=m(√5).Hence a=((m+m(√5))/2)=((m((√5)+1))/2). Since CE is the bisector line of ΔABC ,BCE^(�) =(1/2)ACB^(�_ ) =18° and CE⊥AB,so sin18°=sinBCE^(�) =((BE)/(BC))=(m/2):a=(m/2):((m((√5)+1))/2) =(1/( (√5)+1))=((1×((√5)−1))/(((√(5+1)))((√5)−1)))=(((√5)−1)/4) Thus,sin18°=(((√5)−1)/4) which we need to find

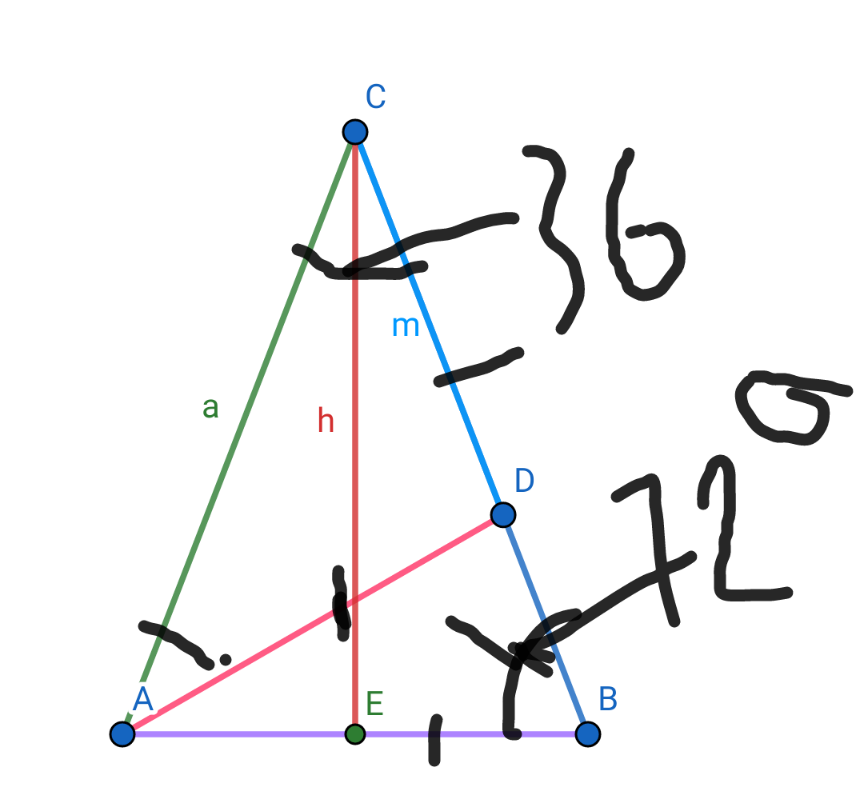
$$\mathrm{Drawing}\:\mathrm{an}\:\mathrm{isosceles}\:\mathrm{triamgle}\:\mathrm{ABC},\mathrm{CA}=\mathrm{CB}=\mathrm{a} \\ $$$$\mathrm{with}\:\widehat {\mathrm{ACB}}=\mathrm{36}°.\mathrm{Then}\:\widehat {\mathrm{CAB}}=\widehat {\mathrm{CBA}}=\mathrm{72}°. \\ $$$$\mathrm{A}\:\mathrm{point}\:\mathrm{D}\:\mathrm{taken}\:\mathrm{on}\:\mathrm{the}\:\mathrm{side}\:\mathrm{BC}\:\mathrm{such}\:\mathrm{that} \\ $$$$\mathrm{DA}=\mathrm{DC}=\mathrm{m}.\mathrm{Denote}\:\mathrm{the}\:\mathrm{midpoont}\:\mathrm{of}\: \\ $$$$\mathrm{side}\:\mathrm{AB}\:\mathrm{by}\:\mathrm{E}.\mathrm{Then}\:\mathrm{we}\:\mathrm{get}\:\widehat {\mathrm{DCA}}=\widehat {\mathrm{DAC}}=\mathrm{36}° \\ $$$$\Rightarrow\widehat {\mathrm{DAB}}=\mathrm{72}°−\mathrm{36}°=\mathrm{36}°\Rightarrow\widehat {\mathrm{ADB}}=\mathrm{72}°,\mathrm{so} \\ $$$$\Delta\mathrm{ABD}\:\mathrm{is}\:\mathrm{isosceles}\:\mathrm{at}\:\mathrm{A}\Rightarrow\mathrm{AB}=\mathrm{AD}=\mathrm{m} \\ $$$$\mathrm{and}\:\mathrm{hence}\:\Delta\mathrm{ABD}\backsimeq\Delta\mathrm{CAB}\left(\mathrm{a}.\mathrm{a}\right) \\ $$$$\Rightarrow\frac{\mathrm{AD}}{\mathrm{BC}}=\frac{\mathrm{BD}}{\mathrm{AB}}\Leftrightarrow\frac{\mathrm{m}}{\mathrm{a}}=\frac{\mathrm{a}−\mathrm{m}}{\mathrm{m}}\Leftrightarrow\mathrm{a}^{\mathrm{2}} −\mathrm{am}−\mathrm{m}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{This}\:\mathrm{is}\:\mathrm{a}\:\mathrm{quadratic}\:\mathrm{equation}\:\mathrm{for}\:\mathrm{a}\:\mathrm{with} \\ $$$$\sqrt{\Delta}=\sqrt{\mathrm{m}^{\mathrm{2}} +\mathrm{4m}^{\mathrm{2}} }=\mathrm{m}\sqrt{\mathrm{5}}.\mathrm{Hence} \\ $$$$\mathrm{a}=\frac{\mathrm{m}+\mathrm{m}\sqrt{\mathrm{5}}}{\mathrm{2}}=\frac{\mathrm{m}\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)}{\mathrm{2}}. \\ $$$$\mathrm{Since}\:\mathrm{CE}\:\mathrm{is}\:\mathrm{the}\:\mathrm{bisector}\:\mathrm{line}\:\mathrm{of}\:\Delta\mathrm{ABC} \\ $$$$,\widehat {\mathrm{BCE}}=\frac{\mathrm{1}}{\mathrm{2}}\widehat {\mathrm{ACB}}=\mathrm{18}°\:\mathrm{and}\:\mathrm{CE}\bot\mathrm{AB},\mathrm{so} \\ $$$$\mathrm{sin18}°=\mathrm{sin}\widehat {\mathrm{BCE}}=\frac{\mathrm{BE}}{\mathrm{BC}}=\frac{\mathrm{m}}{\mathrm{2}}:\mathrm{a}=\frac{\mathrm{m}}{\mathrm{2}}:\frac{\mathrm{m}\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}+\mathrm{1}}=\frac{\mathrm{1}×\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)}{\left(\sqrt{\mathrm{5}+\mathrm{1}}\right)\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}} \\ $$$$\boldsymbol{\mathrm{Thus}},\boldsymbol{\mathrm{sin}}\mathrm{18}°=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\:\:\boldsymbol{\mathrm{which}}\:\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{need}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{find}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply