Question-104777

Question Number 104777 by Anindita last updated on 23/Jul/20

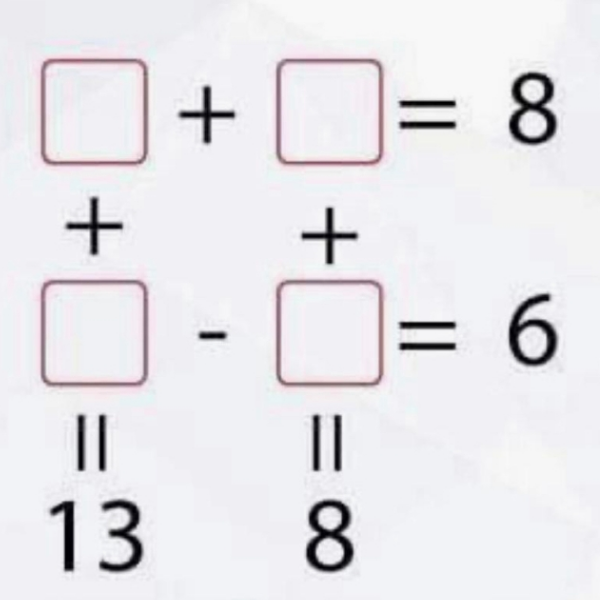
Answered by Aziztisffola last updated on 23/Jul/20

$$\mathrm{3}.\mathrm{5}+\mathrm{4}.\mathrm{5}=\mathrm{8} \\ $$$$+\:\:\:\:\:\:\:\:\:+ \\ $$$$\mathrm{9}.\mathrm{5}−\mathrm{3}.\mathrm{5}=\mathrm{6} \\ $$$$\mathrm{13}\:\:\:\:\:\:\:\:\mathrm{8} \\ $$

Answered by 1549442205PVT last updated on 24/Jul/20

We have the following system of four equations: { ((x+y=8(1))),((z−t=6(2))),((x+z=13(3))),((y+t=8(4))) :} From (1)(4)we get x=t=8−y(5) subtract two eqs.(2)and(3)we get x+t=7⇒2x=2t=7(by (5))⇒x=t=3.5 (4)⇒y=8−3.5=4.5,(2)⇒z=6+t=9.5 Thus,we get (x,y,z,t)=(3.5;4.5;9.5;3.5) determinant (((3.5),+,(4.5),=,8),(+,,+,,),((9.5),−,(3.5),=,6),(=,,=,,),((13),,8,,))

$$\mathrm{We}\:\mathrm{have}\:\mathrm{the}\:\mathrm{following}\:\mathrm{system}\:\mathrm{of}\:\mathrm{four} \\ $$$$\mathrm{equations}:\begin{cases}{\mathrm{x}+\mathrm{y}=\mathrm{8}\left(\mathrm{1}\right)}\\{\mathrm{z}−\mathrm{t}=\mathrm{6}\left(\mathrm{2}\right)}\\{\mathrm{x}+\mathrm{z}=\mathrm{13}\left(\mathrm{3}\right)}\\{\mathrm{y}+\mathrm{t}=\mathrm{8}\left(\mathrm{4}\right)}\end{cases} \\ $$$$\mathrm{From}\:\left(\mathrm{1}\right)\left(\mathrm{4}\right)\mathrm{we}\:\mathrm{get}\:\mathrm{x}=\mathrm{t}=\mathrm{8}−\mathrm{y}\left(\mathrm{5}\right) \\ $$$$\mathrm{subtract}\:\mathrm{two}\:\mathrm{eqs}.\left(\mathrm{2}\right)\mathrm{and}\left(\mathrm{3}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{x}+\mathrm{t}=\mathrm{7}\Rightarrow\mathrm{2x}=\mathrm{2t}=\mathrm{7}\left(\mathrm{by}\:\left(\mathrm{5}\right)\right)\Rightarrow\mathrm{x}=\mathrm{t}=\mathrm{3}.\mathrm{5} \\ $$$$\left(\mathrm{4}\right)\Rightarrow\mathrm{y}=\mathrm{8}−\mathrm{3}.\mathrm{5}=\mathrm{4}.\mathrm{5},\left(\mathrm{2}\right)\Rightarrow\mathrm{z}=\mathrm{6}+\mathrm{t}=\mathrm{9}.\mathrm{5} \\ $$$$\boldsymbol{\mathrm{Thus}},\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{get}}\:\left(\boldsymbol{\mathrm{x}},\boldsymbol{\mathrm{y}},\boldsymbol{\mathrm{z}},\boldsymbol{\mathrm{t}}\right)=\left(\mathrm{3}.\mathrm{5};\mathrm{4}.\mathrm{5};\mathrm{9}.\mathrm{5};\mathrm{3}.\mathrm{5}\right) \\ $$$$\begin{vmatrix}{\mathrm{3}.\mathrm{5}}&{+}&{\mathrm{4}.\mathrm{5}}&{=}&{\mathrm{8}}\\{+}&{}&{+}&{}&{}\\{\mathrm{9}.\mathrm{5}}&{−}&{\mathrm{3}.\mathrm{5}}&{=}&{\mathrm{6}}\\{=}&{}&{=}&{}&{}\\{\mathrm{13}}&{}&{\mathrm{8}}&{}&{}\end{vmatrix} \\ $$

Answered by Rasheed.Sindhi last updated on 24/Jul/20

determinant (( [(( x)),((2x+6=13)),(( x=3 1/2_(−) )) ],→_+ , [(( 8−x)),((8−3 1/2 )),(( 4 1/2)) ],8),(( ↑+),,( ↓+),),( [(( x+6)),(( 3 1/2+6 )),((=9 1/2)) ],←_− , [((8−(8−x))),(( x)),(( 3 1/2)) ],6),((−−−−−−−),−,(−−−−−−),−),(( 13),,( 8),))

$$\begin{vmatrix}{\begin{bmatrix}{\:\:\:\:\:\:\:\:\:\:\:{x}}\\{\mathrm{2}{x}+\mathrm{6}=\mathrm{13}}\\{\underset{−} {\:{x}=\mathrm{3}\:\mathrm{1}/\mathrm{2}}\:\:\:\:\:\:\:\:}\end{bmatrix}}&{\underset{+} {\rightarrow}}&{\begin{bmatrix}{\:\:\:\:\:\mathrm{8}−{x}}\\{\mathrm{8}−\mathrm{3}\:\mathrm{1}/\mathrm{2}\:\:}\\{\:\:\:\:\mathrm{4}\:\mathrm{1}/\mathrm{2}}\end{bmatrix}}&{\mathrm{8}}\\{\:\:\:\:\:\:\:\:\:\:\:\:\uparrow+}&{}&{\:\:\:\:\:\:\:\:\:\:\downarrow+}&{}\\{\begin{bmatrix}{\:\:\:\:\:\:\:\:\:{x}+\mathrm{6}}\\{\:\:\:\:\:\mathrm{3}\:\mathrm{1}/\mathrm{2}+\mathrm{6}\:\:\:\:}\\{=\mathrm{9}\:\mathrm{1}/\mathrm{2}}\end{bmatrix}}&{\underset{−} {\leftarrow}}&{\begin{bmatrix}{\mathrm{8}−\left(\mathrm{8}−{x}\right)}\\{\:\:\:\:\:\:\:\:\:{x}}\\{\:\:\:\:\mathrm{3}\:\mathrm{1}/\mathrm{2}}\end{bmatrix}}&{\mathrm{6}}\\{−−−−−−−}&{−}&{−−−−−−}&{−}\\{\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{13}}&{}&{\:\:\:\:\:\:\:\:\:\:\:\mathrm{8}}&{}\end{vmatrix} \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply