Question Number 104799 by mathocean1 last updated on 23/Jul/20
Commented by mathocean1 last updated on 23/Jul/20

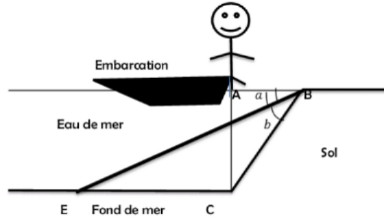
$${I}\:{is}\:{the}\:{point}\:{of}\:{intersection}\:{of}\:\left({AC}\right)\:\: \\ $$$${and}\:\left({BE}\right). \\ $$$${Given}\:{AC}=\mathrm{10}\sqrt{\mathrm{3}}\:{m}\:\:{and}\:{AB}=\mathrm{10}{m}. \\ $$$$\left.\mathrm{1}\right)\:{Determinate}\:{AI}\:{in}\:{each}\:{case}: \\ $$$$\left.{a}\right)\:{a}=\mathrm{2}{b} \\ $$$$\left.{b}\right){tana}=\sqrt{\mathrm{2}}{tanb} \\ $$$$\left.\mathrm{2}\right)\:{At}\:{which}\:{minimal}\:{distance}\:{from} \\ $$$${B}\:{the}\:{man}\:{could}\:{jump}\:{and}\:{touch}\: \\ $$$${the}\:{bottom}\:{of}\:{sea}\:\left({water}\right)\:{without}\: \\ $$$${touvhing}\:{the}\:{line}\:\left({EB}\right)\:{such}\:{that}: \\ $$$${sina}=\mathrm{3}{cosb}\:{and}\:{tanb}=\mathrm{2}{tana}\:? \\ $$
