Question Number 104841 by bramlex last updated on 24/Jul/20

Commented by 1549442205PVT last updated on 24/Jul/20

$$\mathrm{please},\mathrm{who}\:\mathrm{can}\:\mathrm{translate}\:\mathrm{this} \\ $$$$\mathrm{language}\:\mathrm{to}\:\mathrm{English}\:\mathrm{or}\:\mathrm{tell}\:\mathrm{me}\:\mathrm{it}\:\mathrm{is} \\ $$$$\mathrm{what}\:\:\mathrm{language}\:\mathrm{so}\:\mathrm{i}\:\mathrm{can}\:\mathrm{get}\:\mathrm{help}\:\mathrm{from} \\ $$$$\mathrm{other}\:\mathrm{person}. \\ $$
Commented by $@y@m last updated on 24/Jul/20

$${I}\:{think}\:{translation}\:{is}\:{not}\:{required}. \\ $$$${I}\:{don}'{t}\:{know}\:{this}\:{language}\:{literally}, \\ $$$${but}\:{understood}\:{the}\:{question}\:{and} \\ $$$${solved}\:{it}\:{because}\:{it}\:{has}\:{universal} \\ $$$${language}\:{of}\:{Math}. \\ $$
Commented by 1549442205PVT last updated on 24/Jul/20

$$\mathrm{That}\:\mathrm{seems}\:\mathrm{from}\:\mathrm{Uzbek}\:\mathrm{language} \\ $$$$.\mathrm{Don}'\mathrm{t}\:\mathrm{know}\:\:\mathrm{what}\:\mathrm{is}\:\mathrm{question}\:\mathrm{of} \\ $$$$\mathrm{problem}.\mathrm{You}\:\mathrm{have}\:\mathrm{a}\:\mathrm{good}\:\mathrm{guess} \\ $$
Answered by john santu last updated on 24/Jul/20
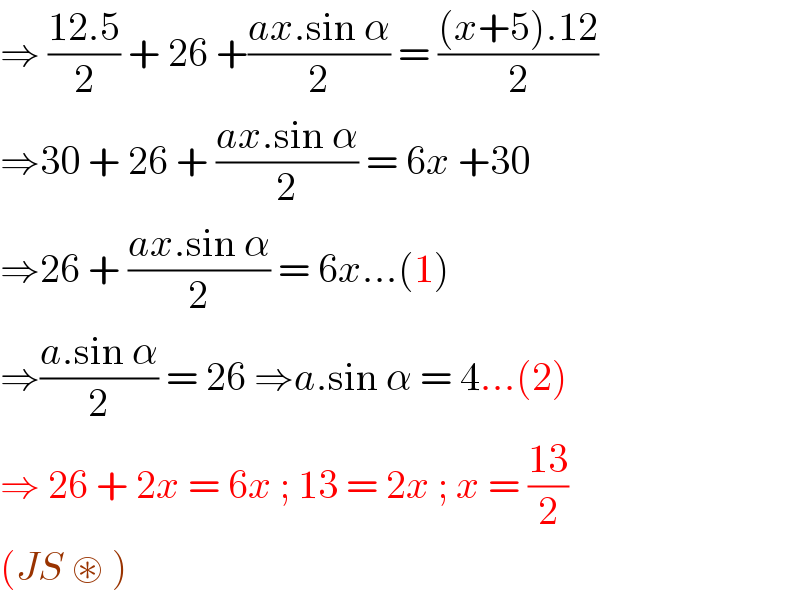
$$\Rightarrow\:\frac{\mathrm{12}.\mathrm{5}}{\mathrm{2}}\:+\:\mathrm{26}\:+\frac{{ax}.\mathrm{sin}\:\alpha}{\mathrm{2}}\:=\:\frac{\left({x}+\mathrm{5}\right).\mathrm{12}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{30}\:+\:\mathrm{26}\:+\:\frac{{ax}.\mathrm{sin}\:\alpha}{\mathrm{2}}\:=\:\mathrm{6}{x}\:+\mathrm{30} \\ $$$$\Rightarrow\mathrm{26}\:+\:\frac{{ax}.\mathrm{sin}\:\alpha}{\mathrm{2}}\:=\:\mathrm{6}{x}…\left(\mathrm{1}\right) \\ $$$$\Rightarrow\frac{{a}.\mathrm{sin}\:\alpha}{\mathrm{2}}\:=\:\mathrm{26}\:\Rightarrow{a}.\mathrm{sin}\:\alpha\:=\:\mathrm{4}…\left(\mathrm{2}\right) \\ $$$$\Rightarrow\:\mathrm{26}\:+\:\mathrm{2}{x}\:=\:\mathrm{6}{x}\:;\:\mathrm{13}\:=\:\mathrm{2}{x}\:;\:{x}\:=\:\frac{\mathrm{13}}{\mathrm{2}} \\ $$$$\left({JS}\:\circledast\:\right)\: \\ $$
Commented by bramlex last updated on 24/Jul/20

$${thank}\:{you}\:\clubsuit \\ $$
Answered by $@y@m last updated on 24/Jul/20
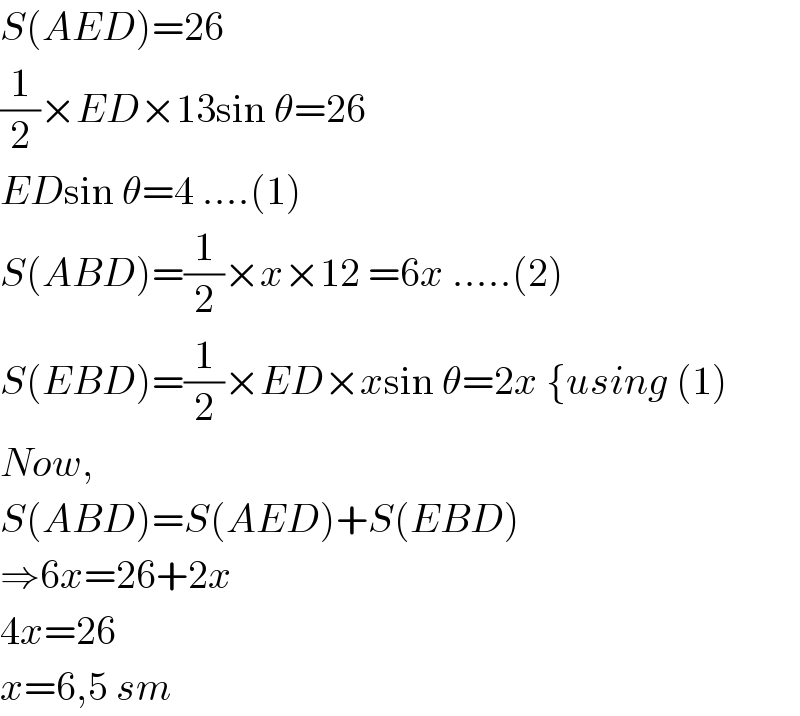
$${S}\left({AED}\right)=\mathrm{26} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×{ED}×\mathrm{13sin}\:\theta=\mathrm{26} \\ $$$${ED}\mathrm{sin}\:\theta=\mathrm{4}\:….\left(\mathrm{1}\right) \\ $$$${S}\left({ABD}\right)=\frac{\mathrm{1}}{\mathrm{2}}×{x}×\mathrm{12}\:=\mathrm{6}{x}\:…..\left(\mathrm{2}\right) \\ $$$${S}\left({EBD}\right)=\frac{\mathrm{1}}{\mathrm{2}}×{ED}×{x}\mathrm{sin}\:\theta=\mathrm{2}{x}\:\left\{{using}\:\left(\mathrm{1}\right)\right. \\ $$$${Now}, \\ $$$${S}\left({ABD}\right)={S}\left({AED}\right)+{S}\left({EBD}\right) \\ $$$$\Rightarrow\mathrm{6}{x}=\mathrm{26}+\mathrm{2}{x} \\ $$$$\mathrm{4}{x}=\mathrm{26} \\ $$$${x}=\mathrm{6},\mathrm{5}\:{sm} \\ $$
Commented by bramlex last updated on 24/Jul/20

$${thank}\:{you}\:\spadesuit \\ $$
Answered by 1549442205PVT last updated on 24/Jul/20

$$\mathrm{If}\:\mathrm{question}\:\mathrm{of}\:\mathrm{problem}\:\mathrm{being}\:\mathrm{find}\:\mathrm{the}\:\mathrm{length}\:\mathrm{x}\:\mathrm{of}\:\mathrm{segment}\:\mathrm{BD}: \\ $$$$\mathrm{AC}=\sqrt{\mathrm{AD}^{\mathrm{2}} −\mathrm{CD}^{\mathrm{2}} }=\sqrt{\mathrm{13}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} }=\sqrt{\mathrm{144}}=\mathrm{12cm}^{\mathrm{2}} \\ $$$$\mathrm{S}\left(\mathrm{ABD}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{BD}×\mathrm{AC}=\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{x}.\mathrm{12}=\mathrm{6x}\left(\mathrm{cm}^{\mathrm{2}} \right) \\ $$$$\mathrm{DE}\:\mathrm{is}\:\mathrm{the}\:\mathrm{bisector}\:\mathrm{so}\:\:\frac{\mathrm{AE}}{\mathrm{EB}}=\frac{\mathrm{AD}}{\mathrm{BD}}=\frac{\mathrm{13}}{\mathrm{x}} \\ $$$$\frac{\mathrm{S}\left(\mathrm{AED}\right)}{\mathrm{S}\left(\mathrm{BED}\right)}=\frac{\mathrm{2S}\left(\mathrm{AED}\right)}{\mathrm{2S}\left(\mathrm{BED}\right)}=\frac{\mathrm{DA}.\mathrm{DEsin}\theta}{\mathrm{DB}.\mathrm{DEsin}\theta}=\frac{\mathrm{AD}}{\mathrm{BD}}=\frac{\mathrm{13}}{\mathrm{x}} \\ $$$$\Rightarrow\frac{\mathrm{26}}{\mathrm{6x}−\mathrm{26}}=\frac{\mathrm{13}}{\mathrm{x}}\Leftrightarrow\mathrm{26x}=\mathrm{78x}−\mathrm{338} \\ $$$$\Rightarrow\mathrm{52x}=\mathrm{338}\Leftrightarrow\mathrm{x}=\frac{\mathrm{338}}{\mathrm{52}}=\mathrm{6},\mathrm{5}\:\mathrm{cm} \\ $$$$\boldsymbol{\mathrm{Hence}},\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{choose}}\:\boldsymbol{\mathrm{answer}}\:\boldsymbol{\mathrm{D}}\left(\mathrm{6},\mathrm{5}\right) \\ $$
