Question Number 104905 by mohammad17 last updated on 24/Jul/20

Answered by OlafThorendsen last updated on 24/Jul/20

$${x}^{\mathrm{4}} +{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1}\:=\:\mathrm{0} \\ $$$$\frac{\mathrm{1}−{x}^{\mathrm{5}} }{\mathrm{1}−{x}}\:=\:\mathrm{0} \\ $$$${x}^{\mathrm{5}} \:=\:\mathrm{1} \\ $$$${x}\:=\:{e}^{\frac{\mathrm{2}{ik}\pi}{\mathrm{5}}} ,\:{k}\in\left\{\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}\right\} \\ $$
Answered by ajfour last updated on 24/Jul/20
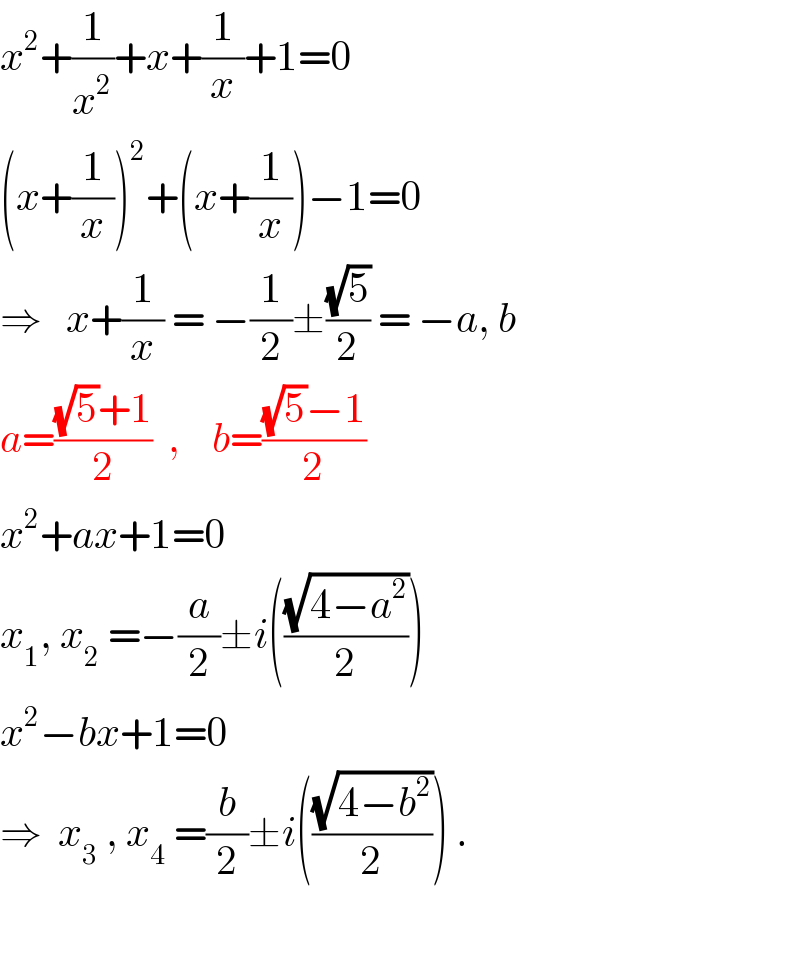
$${x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+{x}+\frac{\mathrm{1}}{{x}}+\mathrm{1}=\mathrm{0}\: \\ $$$$\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\left({x}+\frac{\mathrm{1}}{{x}}\right)−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:{x}+\frac{\mathrm{1}}{{x}}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\:=\:−{a},\:{b} \\ $$$${a}=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}\:\:,\:\:\:\:{b}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +{ax}+\mathrm{1}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} ,\:{x}_{\mathrm{2}} \:=−\frac{{a}}{\mathrm{2}}\pm{i}\left(\frac{\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }}{\mathrm{2}}\right) \\ $$$${x}^{\mathrm{2}} −{bx}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:{x}_{\mathrm{3}} \:,\:{x}_{\mathrm{4}} \:=\frac{{b}}{\mathrm{2}}\pm{i}\left(\frac{\sqrt{\mathrm{4}−{b}^{\mathrm{2}} }}{\mathrm{2}}\right)\:. \\ $$$$ \\ $$
Answered by 1549442205PVT last updated on 25/Jul/20

$$\Leftrightarrow\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\frac{\mathrm{1}}{\mathrm{4}}\right)+\frac{\mathrm{3x}^{\mathrm{2}} }{\mathrm{4}}+\mathrm{x}+\mathrm{1}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\left(\frac{\mathrm{x}}{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{This}\:\mathrm{equation}\:\mathrm{has}\:\mathrm{no}\:\mathrm{real}\:\mathrm{solutions} \\ $$$$\mathrm{because}\:\mathrm{LHS}\:\mathrm{is}\:\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{non}−\mathrm{negative}\:\mathrm{terms}\:\mathrm{and}\:\mathrm{they}\:\mathrm{isn}'\mathrm{t} \\ $$$$\mathrm{equal}\:\mathrm{to}\:\mathrm{zero}\:\mathrm{simultaneously} \\ $$
Commented by 1549442205PVT last updated on 25/Jul/20

$$\mathrm{but}\:\:\mathrm{that}\:\mathrm{steps}\:\mathrm{isn}'\mathrm{t}\:\mathrm{key}\:. \\ $$
Commented by Rasheed.Sindhi last updated on 25/Jul/20
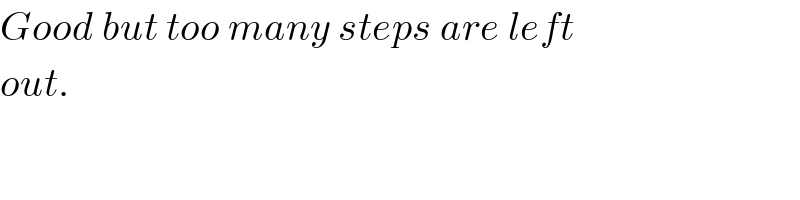
$${Good}\:{but}\:{too}\:{many}\:{steps}\:{are}\:{left} \\ $$$${out}. \\ $$
Commented by Rasheed.Sindhi last updated on 25/Jul/20

$${Yet}\:{an}\:{important}\:{step}. \\ $$$${If}\:{you}\:\mathrm{we}{re}\:{tronsforming}\:{from} \\ $$$$\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\frac{\mathrm{1}}{\mathrm{4}}\right)+\frac{\mathrm{3x}^{\mathrm{2}} }{\mathrm{4}}+\mathrm{x}+\mathrm{1}=\mathrm{0}\:{to} \\ $$$$\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\:{no}\:{step}\:{were} \\ $$$${necessary}. \\ $$$${But}\:{if}\:{you}\:{do}\:{oppositely}\:{I}\:{think} \\ $$$${some}\:{steps}\:{are}\:{necessary}\:{to}\:{insert}. \\ $$$$ \\ $$
