Menu Close

Question-104998

Tinku Tara 0 Comments
Pin




Question Number 104998 by mathocean1 last updated on 25/Jul/20
Commented by mathocean1 last updated on 25/Jul/20
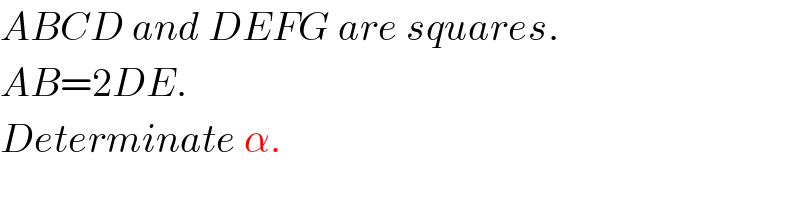
ABCD and DEFG are squares. AB=2DE. Determinate α.
$${ABCD}\:{and}\:{DEFG}\:{are}\:{squares}. \\ $$$${AB}=\mathrm{2}{DE}. \\ $$$${Determinate}\:\alpha. \\ $$
Commented by ajfour last updated on 25/Jul/20
many unnecessary constructions make question confusing..
$${many}\:{unnecessary}\:{constructions} \\ $$$${make}\:{question}\:{confusing}.. \\ $$
Answered by 1549442205PVT last updated on 25/Jul/20
Commented by 1549442205PVT last updated on 25/Jul/20
Putting AB=2a⇒DE=a.Denote by I intersection point of the ray AE and the circle (O) From Pithago′s theorem we get AE=(√(AD^2 +DE^2 )) =a(√5).(1) From the relation formular in circle we get EC.ED=EA.EI⇔a^2 =a(√5).EI ⇒EI=(a/( (√5))). we have ((EI)/(ED))=((EF)/(AE))=(1/( (√5))).It follows that ΔAOE⋍ΔFIE(s.a.s)⇒EIF^(�) =AOE^(�) =135° On the other hands,AIB^(�) =ADB^(�) =45° ⇒AIB^(�) +EIF^(�) =45°+135°=180°.This shows that E,I,B are colinear(q.e.d)
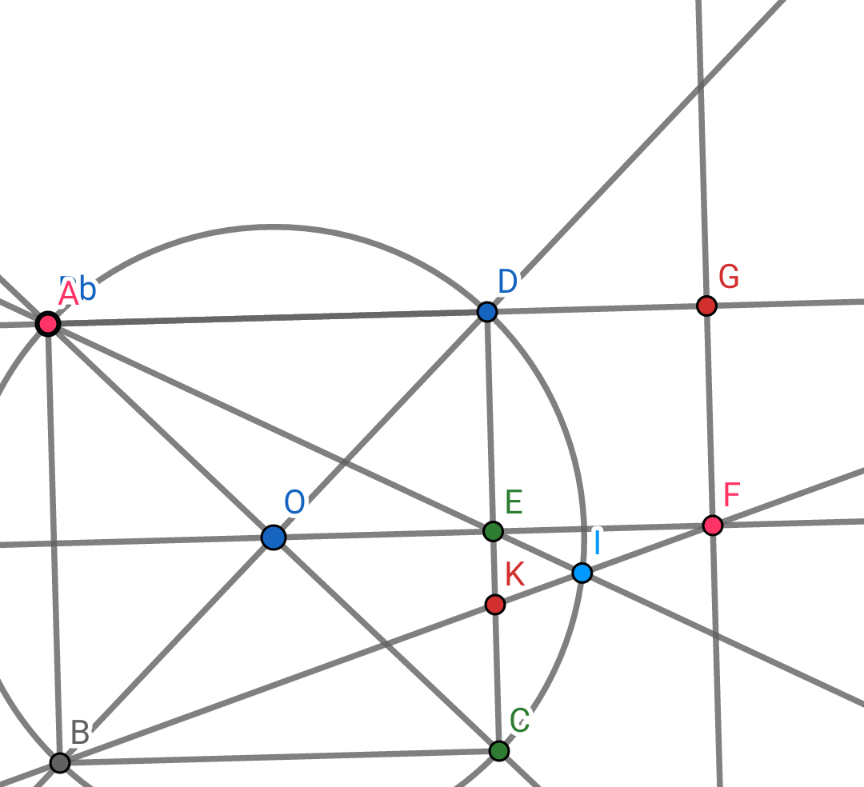
$$ \\ $$$$\mathrm{Putting}\:\mathrm{AB}=\mathrm{2a}\Rightarrow\mathrm{DE}=\mathrm{a}.\mathrm{Denote}\:\mathrm{by}\:\mathrm{I} \\ $$$$\mathrm{intersection}\:\mathrm{point}\:\mathrm{of}\:\mathrm{the}\:\mathrm{ray}\:\mathrm{AE}\:\mathrm{and} \\ $$$$\mathrm{the}\:\mathrm{circle}\:\left(\mathrm{O}\right) \\ $$$$\mathrm{From}\:\mathrm{Pithago}'\mathrm{s}\:\mathrm{theorem}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{AE}=\sqrt{\mathrm{AD}^{\mathrm{2}} +\mathrm{DE}^{\mathrm{2}} }\:=\mathrm{a}\sqrt{\mathrm{5}}.\left(\mathrm{1}\right) \\ $$$$\mathrm{From}\:\mathrm{the}\:\mathrm{relation}\:\mathrm{formular}\:\mathrm{in}\:\mathrm{circle}\:\mathrm{we} \\ $$$$\mathrm{get}\:\mathrm{EC}.\mathrm{ED}=\mathrm{EA}.\mathrm{EI}\Leftrightarrow\mathrm{a}^{\mathrm{2}} =\mathrm{a}\sqrt{\mathrm{5}}.\mathrm{EI} \\ $$$$\Rightarrow\mathrm{EI}=\frac{\mathrm{a}}{\:\sqrt{\mathrm{5}}}. \\ $$$$\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{EI}}{\mathrm{ED}}=\frac{\mathrm{EF}}{\mathrm{AE}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}.\mathrm{It}\:\mathrm{follows}\:\mathrm{that} \\ $$$$\Delta\mathrm{AOE}\backsimeq\Delta\mathrm{FIE}\left(\mathrm{s}.\mathrm{a}.\mathrm{s}\right)\Rightarrow\widehat {\mathrm{EIF}}=\widehat {\mathrm{AOE}}=\mathrm{135}° \\ $$$$\mathrm{On}\:\mathrm{the}\:\mathrm{other}\:\mathrm{hands},\widehat {\mathrm{AIB}}=\widehat {\mathrm{ADB}}=\mathrm{45}° \\ $$$$\Rightarrow\widehat {\mathrm{AIB}}+\widehat {\mathrm{EIF}}=\mathrm{45}°+\mathrm{135}°=\mathrm{180}°.\mathrm{This}\: \\ $$$$\mathrm{shows}\:\mathrm{that}\:\mathrm{E},\mathrm{I},\mathrm{B}\:\mathrm{are}\:\mathrm{colinear}\left(\mathrm{q}.\mathrm{e}.\mathrm{d}\right) \\ $$
Commented by mathocean1 last updated on 25/Jul/20
thank you sir.
$${thank}\:{you}\:{sir}. \\ $$
Answered by mr W last updated on 25/Jul/20
Commented by mr W last updated on 25/Jul/20
tan β=(1/3) tan γ=(1/2) α=β+γ tan α=tan (β+γ)=(((1/3)+(1/2))/(1−(1/3)×(1/2)))=1 ⇒α=45° ∠AIB=α=∠ACB=45° ⇒I is on the circle. BD is diameter of circle, ⇒ΔBDI is right angled triangle, ⇒DI⊥BI
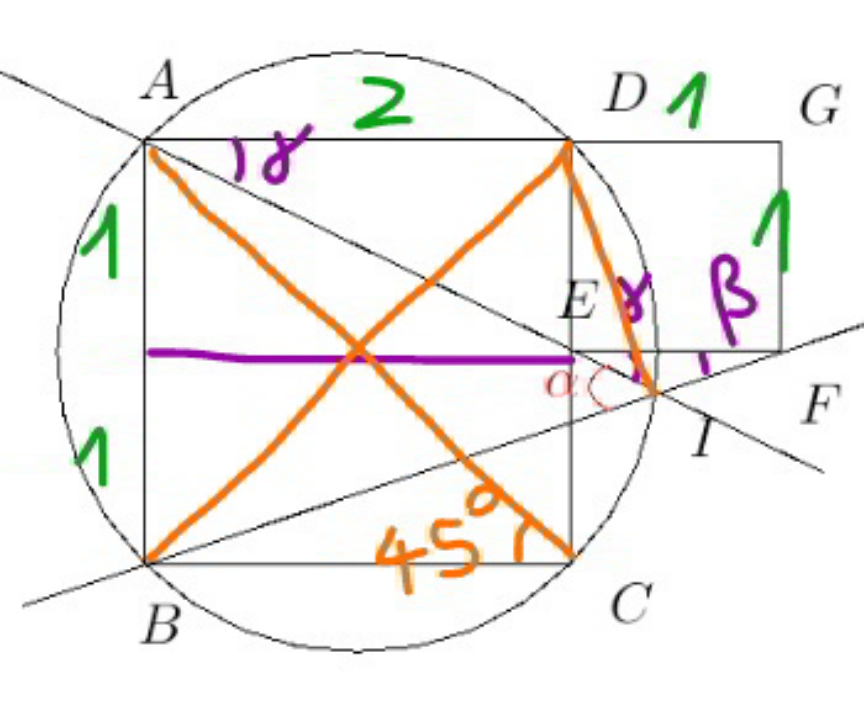
$$\mathrm{tan}\:\beta=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{tan}\:\gamma=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\alpha=\beta+\gamma \\ $$$$\mathrm{tan}\:\alpha=\mathrm{tan}\:\left(\beta+\gamma\right)=\frac{\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{2}}}=\mathrm{1} \\ $$$$\Rightarrow\alpha=\mathrm{45}° \\ $$$$\angle{AIB}=\alpha=\angle{ACB}=\mathrm{45}° \\ $$$$\Rightarrow{I}\:{is}\:{on}\:{the}\:{circle}. \\ $$$$ \\ $$$${BD}\:{is}\:{diameter}\:{of}\:{circle}, \\ $$$$\Rightarrow\Delta{BDI}\:{is}\:{right}\:{angled}\:{triangle}, \\ $$$$\Rightarrow{DI}\bot{BI} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *