Question Number 105001 by ajfour last updated on 25/Jul/20
Commented by ajfour last updated on 25/Jul/20
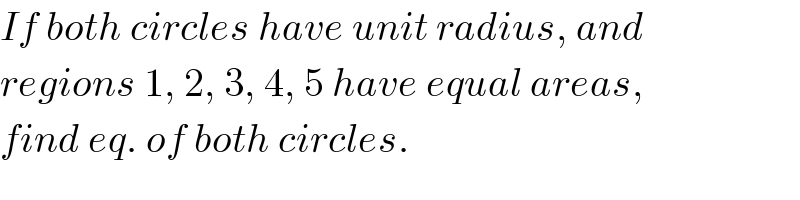
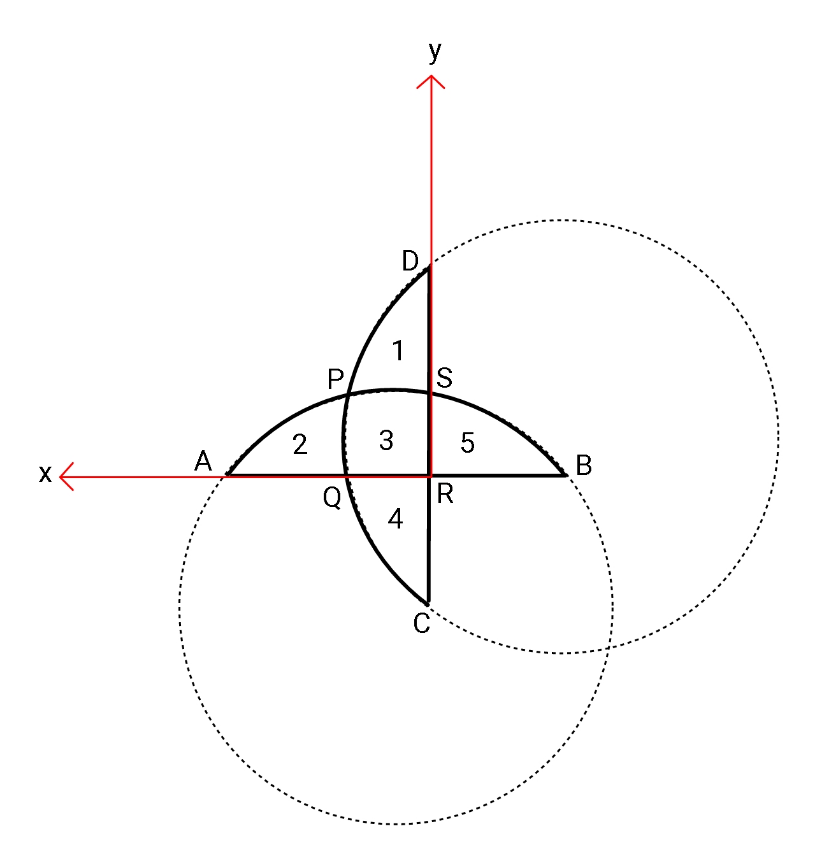
$${If}\:{both}\:{circles}\:{have}\:{unit}\:{radius},\:{and} \\ $$$${regions}\:\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{4},\:\mathrm{5}\:{have}\:{equal}\:{areas}, \\ $$$${find}\:{eq}.\:{of}\:{both}\:{circles}. \\ $$
Answered by ajfour last updated on 25/Jul/20
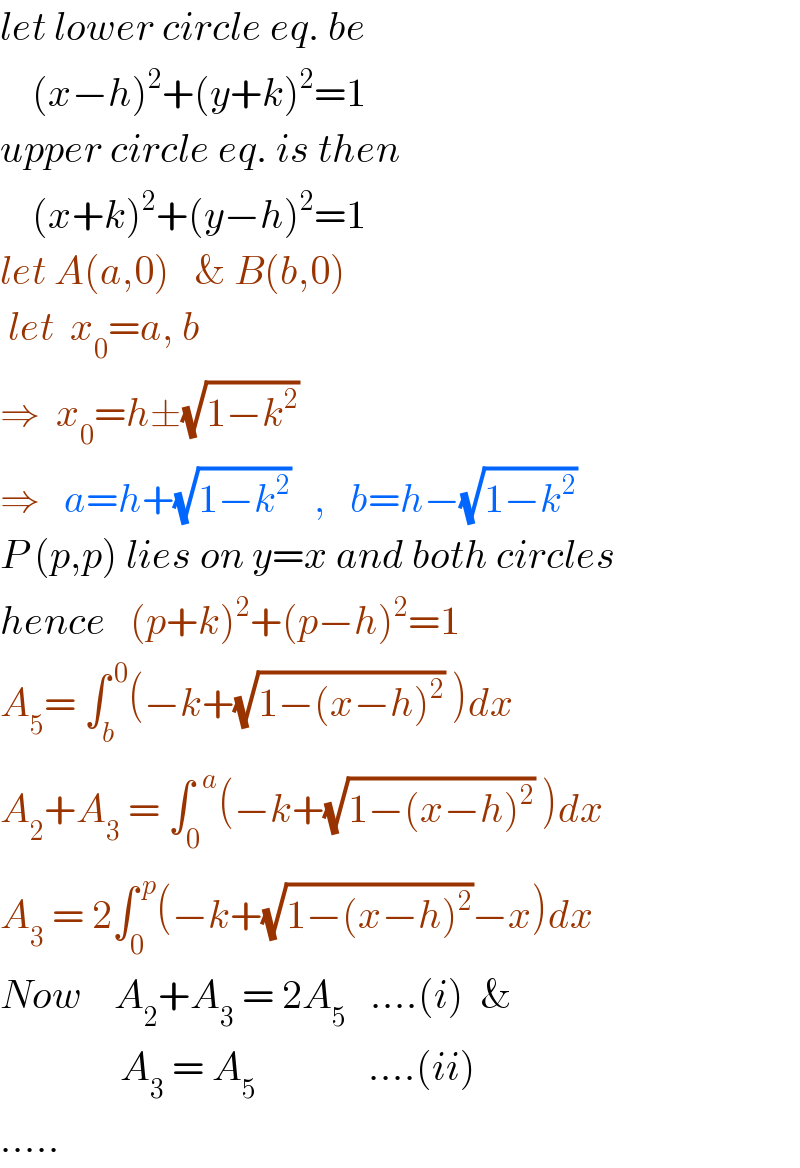
$${let}\:{lower}\:{circle}\:{eq}.\:{be} \\ $$$$\:\:\:\:\left({x}−{h}\right)^{\mathrm{2}} +\left({y}+{k}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$${upper}\:{circle}\:{eq}.\:{is}\:{then} \\ $$$$\:\:\:\:\left({x}+{k}\right)^{\mathrm{2}} +\left({y}−{h}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$${let}\:{A}\left({a},\mathrm{0}\right)\:\:\:\&\:{B}\left({b},\mathrm{0}\right) \\ $$$$\:{let}\:\:{x}_{\mathrm{0}} ={a},\:{b} \\ $$$$\Rightarrow\:\:{x}_{\mathrm{0}} ={h}\pm\sqrt{\mathrm{1}−{k}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\:{a}={h}+\sqrt{\mathrm{1}−{k}^{\mathrm{2}} }\:\:\:,\:\:\:{b}={h}−\sqrt{\mathrm{1}−{k}^{\mathrm{2}} }\: \\ $$$${P}\:\left({p},{p}\right)\:{lies}\:{on}\:{y}={x}\:{and}\:{both}\:{circles} \\ $$$${hence}\:\:\:\left({p}+{k}\right)^{\mathrm{2}} +\left({p}−{h}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$${A}_{\mathrm{5}} =\:\int_{{b}} ^{\:\mathrm{0}} \left(−{k}+\sqrt{\mathrm{1}−\left({x}−{h}\right)^{\mathrm{2}} }\:\right){dx} \\ $$$${A}_{\mathrm{2}} +{A}_{\mathrm{3}} \:=\:\int_{\mathrm{0}} ^{\:\:{a}} \left(−{k}+\sqrt{\mathrm{1}−\left({x}−{h}\right)^{\mathrm{2}} }\:\right){dx} \\ $$$${A}_{\mathrm{3}} \:=\:\mathrm{2}\int_{\mathrm{0}} ^{\:{p}} \left(−{k}+\sqrt{\mathrm{1}−\left({x}−{h}\right)^{\mathrm{2}} }−{x}\right){dx} \\ $$$${Now}\:\:\:\:{A}_{\mathrm{2}} +{A}_{\mathrm{3}} \:=\:\mathrm{2}{A}_{\mathrm{5}} \:\:\:….\left({i}\right)\:\:\& \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{A}_{\mathrm{3}} \:=\:{A}_{\mathrm{5}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:….\left({ii}\right) \\ $$$$….. \\ $$
