Question Number 105057 by I want to learn more last updated on 25/Jul/20

Answered by OlafThorendsen last updated on 25/Jul/20
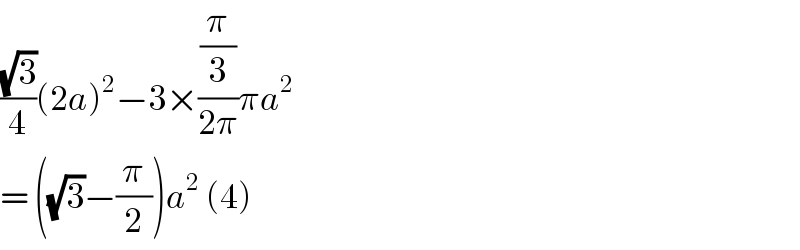
$$\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left(\mathrm{2}{a}\right)^{\mathrm{2}} −\mathrm{3}×\frac{\frac{\pi}{\mathrm{3}}}{\mathrm{2}\pi}\pi{a}^{\mathrm{2}} \\ $$$$=\:\left(\sqrt{\mathrm{3}}−\frac{\pi}{\mathrm{2}}\right){a}^{\mathrm{2}} \:\left(\mathrm{4}\right) \\ $$
Commented by I want to learn more last updated on 25/Jul/20

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$
Answered by Dwaipayan Shikari last updated on 25/Jul/20
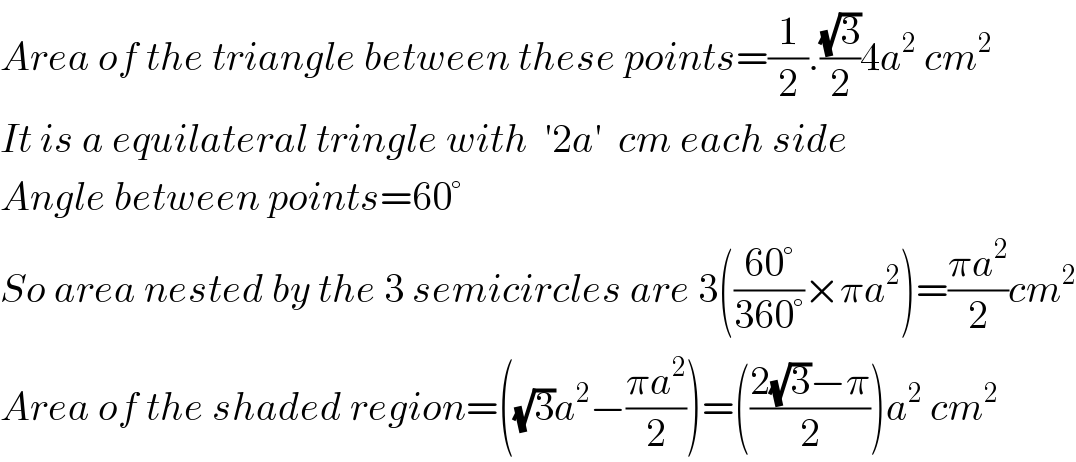
$${Area}\:{of}\:{the}\:{triangle}\:{between}\:{these}\:{points}=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{4}{a}^{\mathrm{2}} \:{cm}^{\mathrm{2}} \\ $$$${It}\:{is}\:{a}\:{equilateral}\:{tringle}\:{with}\:\:'\mathrm{2}{a}'\:\:{cm}\:{each}\:{side} \\ $$$${Angle}\:{between}\:{points}=\mathrm{60}° \\ $$$${So}\:{area}\:{nested}\:{by}\:{the}\:\mathrm{3}\:{semicircles}\:{are}\:\mathrm{3}\left(\frac{\mathrm{60}°}{\mathrm{360}°}×\pi{a}^{\mathrm{2}} \right)=\frac{\pi{a}^{\mathrm{2}} }{\mathrm{2}}{cm}^{\mathrm{2}} \\ $$$${Area}\:{of}\:{the}\:{shaded}\:{region}=\left(\sqrt{\mathrm{3}}{a}^{\mathrm{2}} −\frac{\pi{a}^{\mathrm{2}} }{\mathrm{2}}\right)=\left(\frac{\mathrm{2}\sqrt{\mathrm{3}}−\pi}{\mathrm{2}}\right){a}^{\mathrm{2}} \:{cm}^{\mathrm{2}} \\ $$
Commented by I want to learn more last updated on 25/Jul/20

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
