Question Number 105155 by mohammad17 last updated on 26/Jul/20

Answered by mathmax by abdo last updated on 26/Jul/20
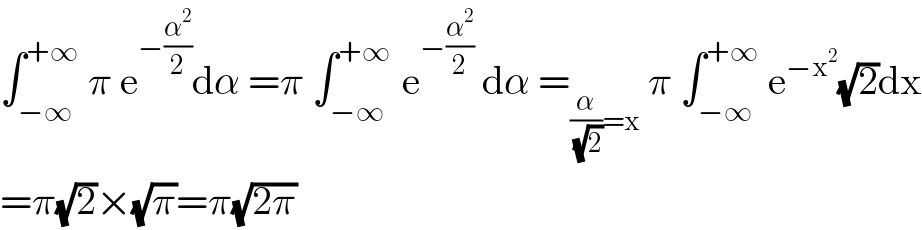
$$\int_{−\infty} ^{+\infty} \:\pi\:\mathrm{e}^{−\frac{\alpha^{\mathrm{2}} }{\mathrm{2}}} \mathrm{d}\alpha\:=\pi\:\int_{−\infty} ^{+\infty\:} \:\mathrm{e}^{−\frac{\alpha^{\mathrm{2}} }{\mathrm{2}}} \:\mathrm{d}\alpha\:=_{\frac{\alpha}{\:\sqrt{\mathrm{2}}}=\mathrm{x}} \:\pi\:\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \sqrt{\mathrm{2}}\mathrm{dx} \\ $$$$=\pi\sqrt{\mathrm{2}}×\sqrt{\pi}=\pi\sqrt{\mathrm{2}\pi} \\ $$
