Question Number 105205 by Ar Brandon last updated on 26/Jul/20

Commented by Aziztisffola last updated on 26/Jul/20
$$\mathrm{ce}\:\mathrm{n}'\mathrm{est}\:\mathrm{pas}\:\mathrm{tres}\:\mathrm{lisible}. \\ $$
Commented by Ar Brandon last updated on 26/Jul/20
D'accord, désolé pour l'inconvenance.
Answered by mathmax by abdo last updated on 27/Jul/20
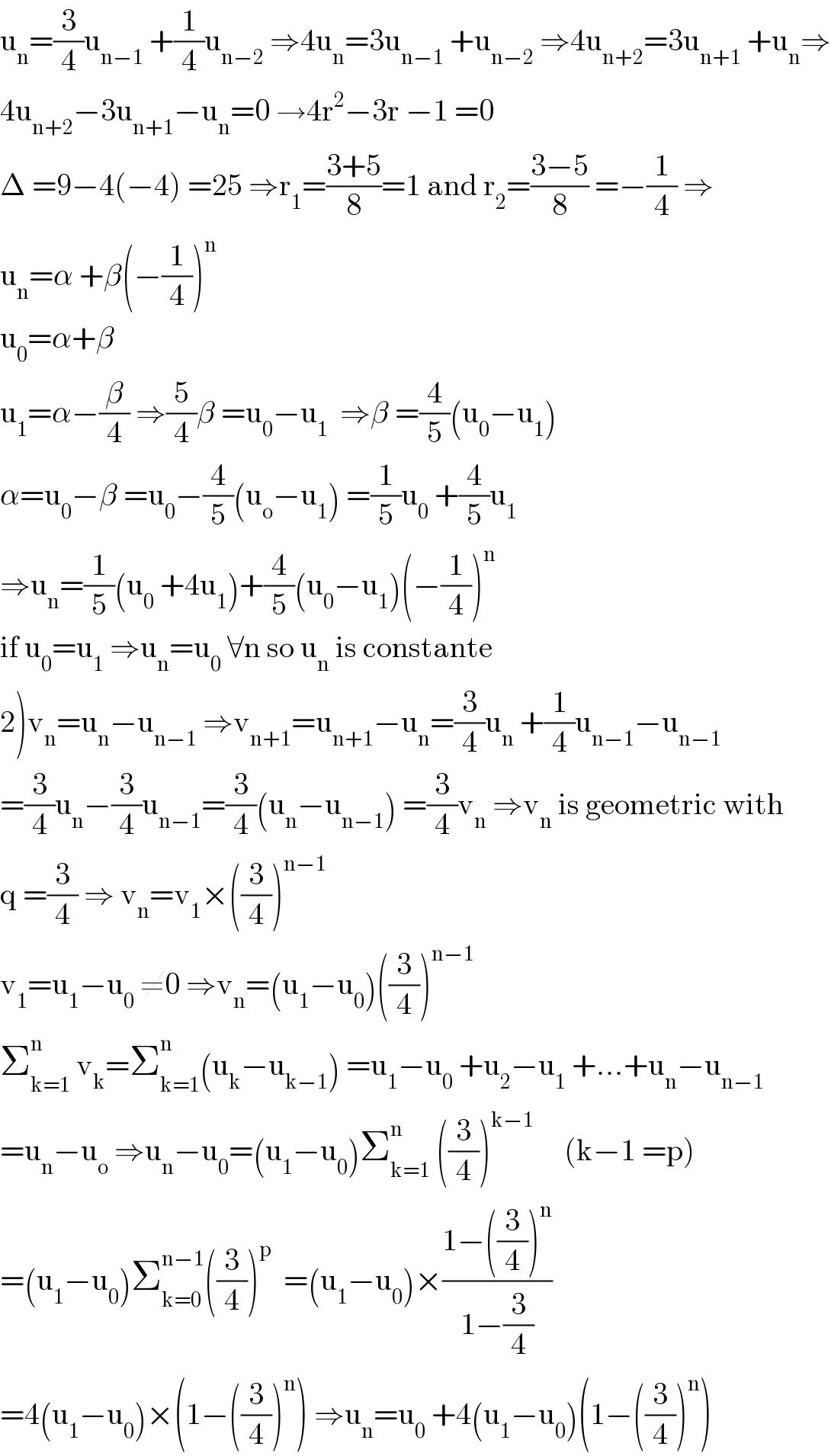
$$\mathrm{u}_{\mathrm{n}} =\frac{\mathrm{3}}{\mathrm{4}}\mathrm{u}_{\mathrm{n}−\mathrm{1}} \:+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{u}_{\mathrm{n}−\mathrm{2}} \:\Rightarrow\mathrm{4u}_{\mathrm{n}} =\mathrm{3u}_{\mathrm{n}−\mathrm{1}} \:+\mathrm{u}_{\mathrm{n}−\mathrm{2}} \:\Rightarrow\mathrm{4u}_{\mathrm{n}+\mathrm{2}} =\mathrm{3u}_{\mathrm{n}+\mathrm{1}} \:+\mathrm{u}_{\mathrm{n}} \Rightarrow \\ $$$$\mathrm{4u}_{\mathrm{n}+\mathrm{2}} −\mathrm{3u}_{\mathrm{n}+\mathrm{1}} −\mathrm{u}_{\mathrm{n}} =\mathrm{0}\:\rightarrow\mathrm{4r}^{\mathrm{2}} −\mathrm{3r}\:−\mathrm{1}\:=\mathrm{0} \\ $$$$\Delta\:=\mathrm{9}−\mathrm{4}\left(−\mathrm{4}\right)\:=\mathrm{25}\:\Rightarrow\mathrm{r}_{\mathrm{1}} =\frac{\mathrm{3}+\mathrm{5}}{\mathrm{8}}=\mathrm{1}\:\mathrm{and}\:\mathrm{r}_{\mathrm{2}} =\frac{\mathrm{3}−\mathrm{5}}{\mathrm{8}}\:=−\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow \\ $$$$\mathrm{u}_{\mathrm{n}} =\alpha\:+\beta\left(−\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{n}} \\ $$$$\mathrm{u}_{\mathrm{0}} =\alpha+\beta \\ $$$$\mathrm{u}_{\mathrm{1}} =\alpha−\frac{\beta}{\mathrm{4}}\:\Rightarrow\frac{\mathrm{5}}{\mathrm{4}}\beta\:=\mathrm{u}_{\mathrm{0}} −\mathrm{u}_{\mathrm{1}} \:\:\Rightarrow\beta\:=\frac{\mathrm{4}}{\mathrm{5}}\left(\mathrm{u}_{\mathrm{0}} −\mathrm{u}_{\mathrm{1}} \right) \\ $$$$\alpha=\mathrm{u}_{\mathrm{0}} −\beta\:=\mathrm{u}_{\mathrm{0}} −\frac{\mathrm{4}}{\mathrm{5}}\left(\mathrm{u}_{\mathrm{o}} −\mathrm{u}_{\mathrm{1}} \right)\:=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{u}_{\mathrm{0}} \:+\frac{\mathrm{4}}{\mathrm{5}}\mathrm{u}_{\mathrm{1}} \\ $$$$\Rightarrow\mathrm{u}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{5}}\left(\mathrm{u}_{\mathrm{0}} \:+\mathrm{4u}_{\mathrm{1}} \right)+\frac{\mathrm{4}}{\mathrm{5}}\left(\mathrm{u}_{\mathrm{0}} −\mathrm{u}_{\mathrm{1}} \right)\left(−\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{n}} \\ $$$$\mathrm{if}\:\mathrm{u}_{\mathrm{0}} =\mathrm{u}_{\mathrm{1}} \:\Rightarrow\mathrm{u}_{\mathrm{n}} =\mathrm{u}_{\mathrm{0}} \:\forall\mathrm{n}\:\mathrm{so}\:\mathrm{u}_{\mathrm{n}} \:\mathrm{is}\:\mathrm{constante} \\ $$$$\left.\mathrm{2}\right)\mathrm{v}_{\mathrm{n}} =\mathrm{u}_{\mathrm{n}} −\mathrm{u}_{\mathrm{n}−\mathrm{1}} \:\Rightarrow\mathrm{v}_{\mathrm{n}+\mathrm{1}} =\mathrm{u}_{\mathrm{n}+\mathrm{1}} −\mathrm{u}_{\mathrm{n}} =\frac{\mathrm{3}}{\mathrm{4}}\mathrm{u}_{\mathrm{n}} \:+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{u}_{\mathrm{n}−\mathrm{1}} −\mathrm{u}_{\mathrm{n}−\mathrm{1}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}\mathrm{u}_{\mathrm{n}} −\frac{\mathrm{3}}{\mathrm{4}}\mathrm{u}_{\mathrm{n}−\mathrm{1}} =\frac{\mathrm{3}}{\mathrm{4}}\left(\mathrm{u}_{\mathrm{n}} −\mathrm{u}_{\mathrm{n}−\mathrm{1}} \right)\:=\frac{\mathrm{3}}{\mathrm{4}}\mathrm{v}_{\mathrm{n}} \:\Rightarrow\mathrm{v}_{\mathrm{n}} \:\mathrm{is}\:\mathrm{geometric}\:\mathrm{with} \\ $$$$\mathrm{q}\:=\frac{\mathrm{3}}{\mathrm{4}}\:\Rightarrow\:\mathrm{v}_{\mathrm{n}} =\mathrm{v}_{\mathrm{1}} ×\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{n}−\mathrm{1}} \\ $$$$\mathrm{v}_{\mathrm{1}} =\mathrm{u}_{\mathrm{1}} −\mathrm{u}_{\mathrm{0}} \:\neq\mathrm{0}\:\Rightarrow\mathrm{v}_{\mathrm{n}} =\left(\mathrm{u}_{\mathrm{1}} −\mathrm{u}_{\mathrm{0}} \right)\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{n}−\mathrm{1}} \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{v}_{\mathrm{k}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(\mathrm{u}_{\mathrm{k}} −\mathrm{u}_{\mathrm{k}−\mathrm{1}} \right)\:=\mathrm{u}_{\mathrm{1}} −\mathrm{u}_{\mathrm{0}} \:+\mathrm{u}_{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} \:+…+\mathrm{u}_{\mathrm{n}} −\mathrm{u}_{\mathrm{n}−\mathrm{1}} \\ $$$$=\mathrm{u}_{\mathrm{n}} −\mathrm{u}_{\mathrm{o}} \:\Rightarrow\mathrm{u}_{\mathrm{n}} −\mathrm{u}_{\mathrm{0}} =\left(\mathrm{u}_{\mathrm{1}} −\mathrm{u}_{\mathrm{0}} \right)\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{k}−\mathrm{1}} \:\:\:\:\:\left(\mathrm{k}−\mathrm{1}\:=\mathrm{p}\right) \\ $$$$=\left(\mathrm{u}_{\mathrm{1}} −\mathrm{u}_{\mathrm{0}} \right)\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{p}} \:\:=\left(\mathrm{u}_{\mathrm{1}} −\mathrm{u}_{\mathrm{0}} \right)×\frac{\mathrm{1}−\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{n}} }{\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$=\mathrm{4}\left(\mathrm{u}_{\mathrm{1}} −\mathrm{u}_{\mathrm{0}} \right)×\left(\mathrm{1}−\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{n}} \right)\:\Rightarrow\mathrm{u}_{\mathrm{n}} =\mathrm{u}_{\mathrm{0}} \:+\mathrm{4}\left(\mathrm{u}_{\mathrm{1}} −\mathrm{u}_{\mathrm{0}} \right)\left(\mathrm{1}−\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{n}} \right) \\ $$
Commented by Ar Brandon last updated on 27/Jul/20
Thanks Sir. Always willing to help ! ��
Commented by abdomathmax last updated on 27/Jul/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir}. \\ $$
