Question Number 105265 by bemath last updated on 27/Jul/20

Answered by Cinezoidy1 last updated on 27/Jul/20
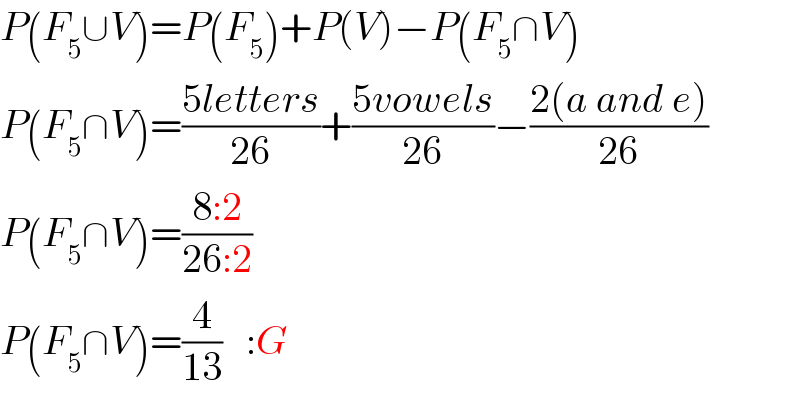
$${P}\left({F}_{\mathrm{5}} \cup{V}\right)={P}\left({F}_{\mathrm{5}} \right)+{P}\left({V}\right)−{P}\left({F}_{\mathrm{5}} \cap{V}\right) \\ $$$${P}\left({F}_{\mathrm{5}} \cap{V}\right)=\frac{\mathrm{5}{letters}}{\mathrm{26}}+\frac{\mathrm{5}{vowels}}{\mathrm{26}}−\frac{\mathrm{2}\left({a}\:{and}\:{e}\right)}{\mathrm{26}} \\ $$$${P}\left({F}_{\mathrm{5}} \cap{V}\right)=\frac{\mathrm{8}:\mathrm{2}}{\mathrm{26}:\mathrm{2}} \\ $$$${P}\left({F}_{\mathrm{5}} \cap{V}\right)=\frac{\mathrm{4}}{\mathrm{13}}\:\:\::{G} \\ $$
Answered by JDamian last updated on 27/Jul/20

$${G}.\:\frac{\mathrm{4}}{\mathrm{13}} \\ $$
Commented by bemath last updated on 27/Jul/20

$${how}? \\ $$
Answered by JDamian last updated on 27/Jul/20

$${The}\:{subset}\:{from}\:{alphabet}\:{is} \\ $$$$\left\{{a},\:{b},\:{c},\:{d},\:{e},\:{i},\:{o},\:{u}\right\} \\ $$$${i}.{e}.\:\mathrm{8}\:{letters}\:{from}\:\mathrm{26} \\ $$$$ \\ $$$$\frac{\mathrm{8}}{\mathrm{26}}\:=\:\frac{\mathrm{4}}{\mathrm{13}} \\ $$
