Menu Close

Question-105266

Tinku Tara 0 Comments
Pin




Question Number 105266 by mohammad17 last updated on 27/Jul/20
Answered by mathmax by abdo last updated on 27/Jul/20
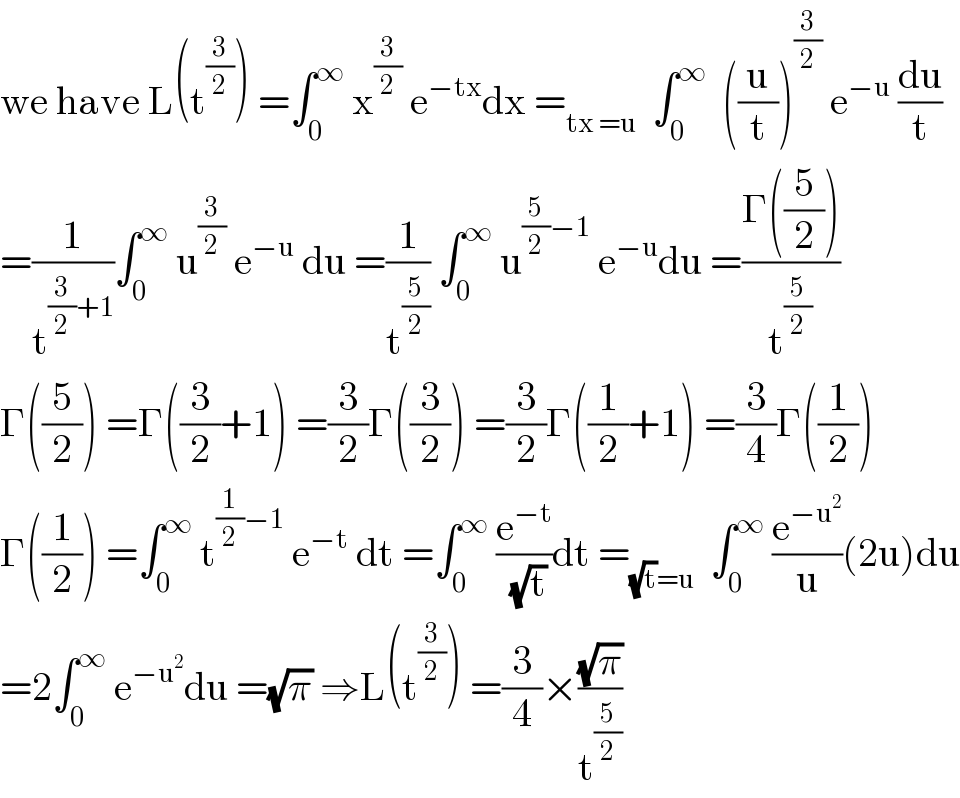
we have L(t^(3/2) ) =∫_0 ^∞ x^(3/2) e^(−tx) dx =_(tx =u) ∫_0 ^∞ ((u/t))^(3/2) e^(−u) (du/t) =(1/t^((3/2)+1) )∫_0 ^∞ u^(3/2) e^(−u) du =(1/t^(5/2) ) ∫_0 ^∞ u^((5/2)−1) e^(−u) du =((Γ((5/2)))/t^(5/2) ) Γ((5/2)) =Γ((3/2)+1) =(3/2)Γ((3/2)) =(3/2)Γ((1/2)+1) =(3/4)Γ((1/2)) Γ((1/2)) =∫_0 ^∞ t^((1/2)−1) e^(−t) dt =∫_0 ^∞ (e^(−t) /( (√t)))dt =_((√t)=u) ∫_0 ^∞ (e^(−u^2 ) /u)(2u)du =2∫_0 ^∞ e^(−u^2 ) du =(√π) ⇒L(t^(3/2) ) =(3/4)×((√π)/t^(5/2) )
$$\mathrm{we}\:\mathrm{have}\:\mathrm{L}\left(\mathrm{t}^{\frac{\mathrm{3}}{\mathrm{2}}} \right)\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \:\mathrm{e}^{−\mathrm{tx}} \mathrm{dx}\:=_{\mathrm{tx}\:=\mathrm{u}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\left(\frac{\mathrm{u}}{\mathrm{t}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\mathrm{e}^{−\mathrm{u}} \:\frac{\mathrm{du}}{\mathrm{t}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{t}^{\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{1}} }\int_{\mathrm{0}} ^{\infty} \:\mathrm{u}^{\frac{\mathrm{3}}{\mathrm{2}}} \:\mathrm{e}^{−\mathrm{u}} \:\mathrm{du}\:=\frac{\mathrm{1}}{\mathrm{t}^{\frac{\mathrm{5}}{\mathrm{2}}} }\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{u}^{\frac{\mathrm{5}}{\mathrm{2}}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{u}} \mathrm{du}\:=\frac{\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}\right)}{\mathrm{t}^{\frac{\mathrm{5}}{\mathrm{2}}} } \\ $$$$\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}\right)\:=\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{1}\right)\:=\frac{\mathrm{3}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\:=\frac{\mathrm{3}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}\right)\:=\frac{\mathrm{3}}{\mathrm{4}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{t}} }{\:\sqrt{\mathrm{t}}}\mathrm{dt}\:=_{\sqrt{\mathrm{t}}=\mathrm{u}} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{u}^{\mathrm{2}} } }{\mathrm{u}}\left(\mathrm{2u}\right)\mathrm{du} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{u}^{\mathrm{2}} } \mathrm{du}\:=\sqrt{\pi}\:\Rightarrow\mathrm{L}\left(\mathrm{t}^{\frac{\mathrm{3}}{\mathrm{2}}} \right)\:=\frac{\mathrm{3}}{\mathrm{4}}×\frac{\sqrt{\pi}}{\mathrm{t}^{\frac{\mathrm{5}}{\mathrm{2}}} } \\ $$
Answered by abdomathmax last updated on 27/Jul/20
L(h(s))=∫_0 ^∞ t^2 sin(2t)e^(−st) dt =Im(∫_0 ^∞ t^2 e^(2it−st) dt) =Im(∫_0 ^∞ t^2 e^((2i−s)t) dt) but by parts ∫_0 ^∞ t^2 e^((2i−s)t) dt =[(t^2 /(2i−s))e^((2i−s)t) ]_(t=0) ^∞ −∫_0 ^∞ 2t .(1/(2i−s))e^((2i−s)t) dt =−(2/(2i−s))∫_0 ^∞ t e^((2i−s)t) dt =((−2)/(2i−s)){ [(t/(2i−s)) e^((2i−s)t) ]_0 ^∞ −∫_0 ^∞ (1/(2i−s))e^((2i−s)t) dt} =(2/((2i−s)^2 ))∫_0 ^∞ e^((2i−s)t) dt =(2/((2i−s)^2 ))[(1/(2i−s))e^((2i−s)t) ]_0 ^∞ =−(2/((2i−s)^3 )) =(2/((s−2i)^3 )) =((2(s+2i)^3 )/((s^2 +4)^3 )) =((2(s^3 +3s^2 (2i) +3s(2i)^2 +(2i)^3 ))/((s^2 +4)^3 )) =((2(s^(3 ) +6is^2 −12s−8i))/((s^2 +4)^3 )) ⇒ Im(...) =((2(6s^2 −8))/((s^2 +4)^3 )) ⇒ F(s) =((4(3s^2 −4))/((s^2 +4)^3 ))
$$\mathrm{L}\left(\mathrm{h}\left(\mathrm{s}\right)\right)=\int_{\mathrm{0}} ^{\infty} \mathrm{t}^{\mathrm{2}} \mathrm{sin}\left(\mathrm{2t}\right)\mathrm{e}^{−\mathrm{st}} \mathrm{dt} \\ $$$$=\mathrm{Im}\left(\int_{\mathrm{0}} ^{\infty} \mathrm{t}^{\mathrm{2}} \:\mathrm{e}^{\mathrm{2it}−\mathrm{st}} \mathrm{dt}\right)\:=\mathrm{Im}\left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{2}} \:\mathrm{e}^{\left(\mathrm{2i}−\mathrm{s}\right)\mathrm{t}} \mathrm{dt}\right)\:\mathrm{but}\:\mathrm{by}\:\mathrm{parts} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{2}} \:\mathrm{e}^{\left(\mathrm{2i}−\mathrm{s}\right)\mathrm{t}} \mathrm{dt}\:\:=\left[\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2i}−\mathrm{s}}\mathrm{e}^{\left(\mathrm{2i}−\mathrm{s}\right)\mathrm{t}} \right]_{\mathrm{t}=\mathrm{0}} ^{\infty} −\int_{\mathrm{0}} ^{\infty} \mathrm{2t}\:.\frac{\mathrm{1}}{\mathrm{2i}−\mathrm{s}}\mathrm{e}^{\left(\mathrm{2i}−\mathrm{s}\right)\mathrm{t}} \mathrm{dt} \\ $$$$=−\frac{\mathrm{2}}{\mathrm{2i}−\mathrm{s}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}\:\mathrm{e}^{\left(\mathrm{2i}−\mathrm{s}\right)\mathrm{t}} \:\mathrm{dt} \\ $$$$=\frac{−\mathrm{2}}{\mathrm{2i}−\mathrm{s}}\left\{\:\left[\frac{\mathrm{t}}{\mathrm{2i}−\mathrm{s}}\:\mathrm{e}^{\left(\mathrm{2i}−\mathrm{s}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{\infty} −\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{2i}−\mathrm{s}}\mathrm{e}^{\left(\mathrm{2i}−\mathrm{s}\right)\mathrm{t}} \mathrm{dt}\right\} \\ $$$$=\frac{\mathrm{2}}{\left(\mathrm{2i}−\mathrm{s}\right)^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\left(\mathrm{2i}−\mathrm{s}\right)\mathrm{t}} \mathrm{dt}\:=\frac{\mathrm{2}}{\left(\mathrm{2i}−\mathrm{s}\right)^{\mathrm{2}} }\left[\frac{\mathrm{1}}{\mathrm{2i}−\mathrm{s}}\mathrm{e}^{\left(\mathrm{2i}−\mathrm{s}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{\infty} \\ $$$$=−\frac{\mathrm{2}}{\left(\mathrm{2i}−\mathrm{s}\right)^{\mathrm{3}} }\:=\frac{\mathrm{2}}{\left(\mathrm{s}−\mathrm{2i}\right)^{\mathrm{3}} }\:=\frac{\mathrm{2}\left(\mathrm{s}+\mathrm{2i}\right)^{\mathrm{3}} }{\left(\mathrm{s}^{\mathrm{2}} \:+\mathrm{4}\right)^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{2}\left(\mathrm{s}^{\mathrm{3}} \:+\mathrm{3s}^{\mathrm{2}} \left(\mathrm{2i}\right)\:+\mathrm{3s}\left(\mathrm{2i}\right)^{\mathrm{2}} \:+\left(\mathrm{2i}\right)^{\mathrm{3}} \right)}{\left(\mathrm{s}^{\mathrm{2}} \:+\mathrm{4}\right)^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{2}\left(\mathrm{s}^{\mathrm{3}\:} \:+\mathrm{6is}^{\mathrm{2}} \:−\mathrm{12s}−\mathrm{8i}\right)}{\left(\mathrm{s}^{\mathrm{2}} \:+\mathrm{4}\right)^{\mathrm{3}} }\:\Rightarrow \\ $$$$\mathrm{Im}\left(…\right)\:=\frac{\mathrm{2}\left(\mathrm{6s}^{\mathrm{2}} −\mathrm{8}\right)}{\left(\mathrm{s}^{\mathrm{2}} \:+\mathrm{4}\right)^{\mathrm{3}} }\:\Rightarrow\:\mathrm{F}\left(\mathrm{s}\right)\:=\frac{\mathrm{4}\left(\mathrm{3s}^{\mathrm{2}} −\mathrm{4}\right)}{\left(\mathrm{s}^{\mathrm{2}} \:+\mathrm{4}\right)^{\mathrm{3}} } \\ $$$$ \\ $$
Answered by Aziztisffola last updated on 27/Jul/20
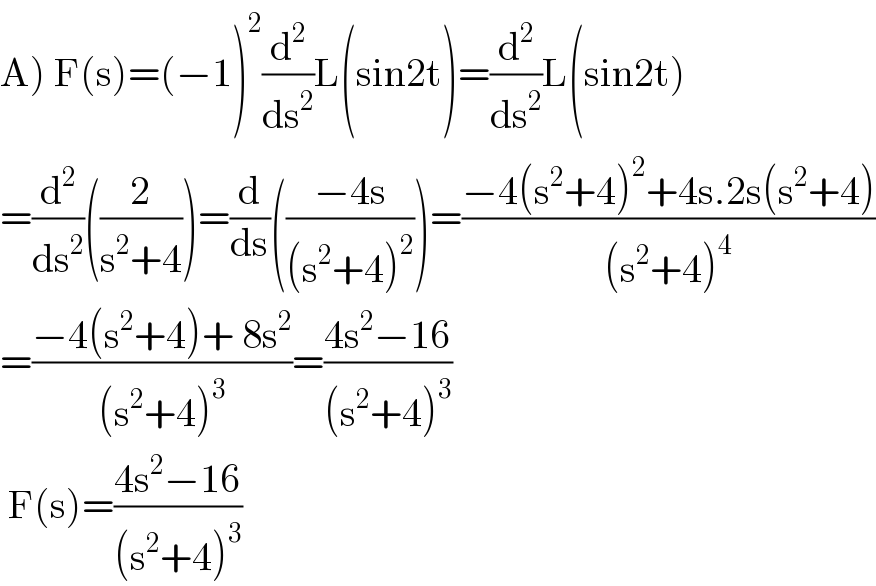
A) F(s)=(−1)^2 (d^2 /ds^2 )L(sin2t)=(d^2 /ds^2 )L(sin2t) =(d^2 /ds^2 )((2/(s^2 +4)))=(d/ds)(((−4s)/((s^2 +4)^2 )))=((−4(s^2 +4)^2 +4s.2s(s^2 +4))/((s^2 +4)^4 )) =((−4(s^2 +4)+ 8s^2 )/((s^2 +4)^3 ))=((4s^2 −16)/((s^2 +4)^3 )) F(s)=((4s^2 −16)/((s^2 +4)^3 ))
$$\left.\mathrm{A}\right)\:\mathrm{F}\left(\mathrm{s}\right)=\left(−\mathrm{1}\right)^{\mathrm{2}} \frac{\mathrm{d}^{\mathrm{2}} }{\mathrm{ds}^{\mathrm{2}} }\mathrm{L}\left(\mathrm{sin2t}\right)=\frac{\mathrm{d}^{\mathrm{2}} }{\mathrm{ds}^{\mathrm{2}} }\mathrm{L}\left(\mathrm{sin2t}\right) \\ $$$$=\frac{\mathrm{d}^{\mathrm{2}} }{\mathrm{ds}^{\mathrm{2}} }\left(\frac{\mathrm{2}}{\mathrm{s}^{\mathrm{2}} +\mathrm{4}}\right)=\frac{\mathrm{d}}{\mathrm{ds}}\left(\frac{−\mathrm{4s}}{\left(\mathrm{s}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} }\right)=\frac{−\mathrm{4}\left(\mathrm{s}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} +\mathrm{4s}.\mathrm{2s}\left(\mathrm{s}^{\mathrm{2}} +\mathrm{4}\right)}{\left(\mathrm{s}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{4}} } \\ $$$$=\frac{−\mathrm{4}\left(\mathrm{s}^{\mathrm{2}} +\mathrm{4}\right)+\:\mathrm{8s}^{\mathrm{2}} }{\left(\mathrm{s}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{3}} }=\frac{\mathrm{4s}^{\mathrm{2}} −\mathrm{16}}{\left(\mathrm{s}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{3}} } \\ $$$$\:\mathrm{F}\left(\mathrm{s}\right)=\frac{\mathrm{4s}^{\mathrm{2}} −\mathrm{16}}{\left(\mathrm{s}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{3}} } \\ $$
Answered by bemath last updated on 27/Jul/20
Answered by Aziztisffola last updated on 27/Jul/20
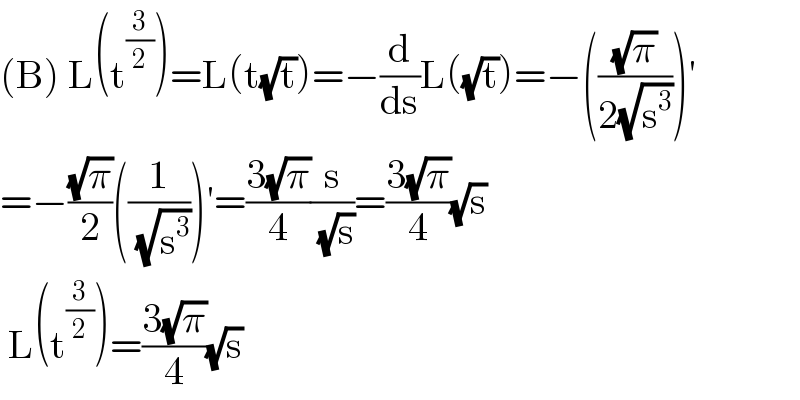
(B) L(t^(3/2) )=L(t(√t))=−(d/ds)L((√t))=−(((√π)/(2(√s^3 ))))′ =−((√π)/2)((1/( (√s^3 ))))′=((3(√π))/4)(s/( (√s)))=((3(√π))/4)(√s) L(t^(3/2) )=((3(√π))/4)(√s)
$$\left(\mathrm{B}\right)\:\mathrm{L}\left(\mathrm{t}^{\frac{\mathrm{3}}{\mathrm{2}}} \right)=\mathrm{L}\left(\mathrm{t}\sqrt{\mathrm{t}}\right)=−\frac{\mathrm{d}}{\mathrm{ds}}\mathrm{L}\left(\sqrt{\mathrm{t}}\right)=−\left(\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{s}^{\mathrm{3}} }}\right)' \\ $$$$=−\frac{\sqrt{\pi}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{s}^{\mathrm{3}} }}\right)'=\frac{\mathrm{3}\sqrt{\pi}}{\mathrm{4}}\frac{\mathrm{s}}{\:\sqrt{\mathrm{s}}}=\frac{\mathrm{3}\sqrt{\pi}}{\mathrm{4}}\sqrt{\mathrm{s}} \\ $$$$\:\mathrm{L}\left(\mathrm{t}^{\frac{\mathrm{3}}{\mathrm{2}}} \right)=\frac{\mathrm{3}\sqrt{\pi}}{\mathrm{4}}\sqrt{\mathrm{s}} \\ $$
Answered by mathmax by abdo last updated on 27/Jul/20
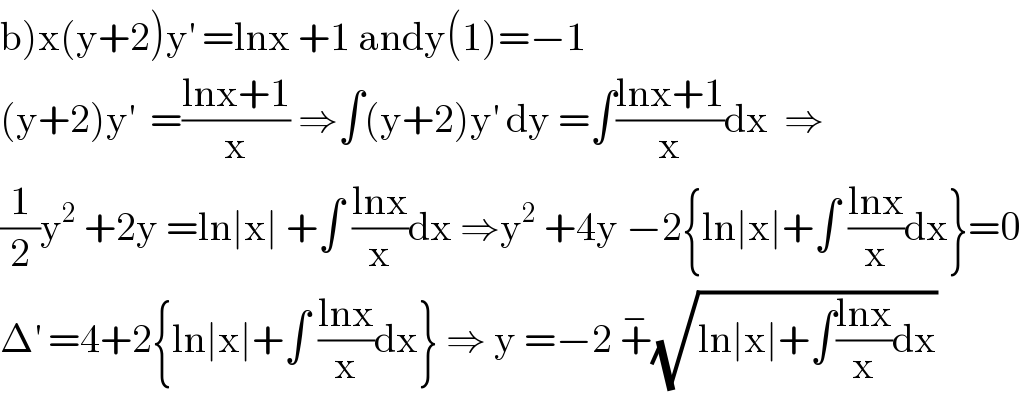
b)x(y+2)y^′ =lnx +1 andy(1)=−1 (y+2)y^′ =((lnx+1)/x) ⇒∫(y+2)y^′ dy =∫((lnx+1)/x)dx ⇒ (1/2)y^2 +2y =ln∣x∣ +∫ ((lnx)/x)dx ⇒y^2 +4y −2{ln∣x∣+∫ ((lnx)/x)dx}=0 Δ^′ =4+2{ln∣x∣+∫ ((lnx)/x)dx} ⇒ y =−2 +^− (√(ln∣x∣+∫((lnx)/x)dx))
$$\left.\mathrm{b}\right)\mathrm{x}\left(\mathrm{y}+\mathrm{2}\right)\mathrm{y}^{'} \:=\mathrm{lnx}\:+\mathrm{1}\:\mathrm{andy}\left(\mathrm{1}\right)=−\mathrm{1} \\ $$$$\left(\mathrm{y}+\mathrm{2}\right)\mathrm{y}^{'} \:\:=\frac{\mathrm{lnx}+\mathrm{1}}{\mathrm{x}}\:\Rightarrow\int\left(\mathrm{y}+\mathrm{2}\right)\mathrm{y}^{'} \:\mathrm{dy}\:=\int\frac{\mathrm{lnx}+\mathrm{1}}{\mathrm{x}}\mathrm{dx}\:\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{y}^{\mathrm{2}} \:+\mathrm{2y}\:=\mathrm{ln}\mid\mathrm{x}\mid\:+\int\:\frac{\mathrm{lnx}}{\mathrm{x}}\mathrm{dx}\:\Rightarrow\mathrm{y}^{\mathrm{2}} \:+\mathrm{4y}\:−\mathrm{2}\left\{\mathrm{ln}\mid\mathrm{x}\mid+\int\:\frac{\mathrm{lnx}}{\mathrm{x}}\mathrm{dx}\right\}=\mathrm{0} \\ $$$$\Delta^{'} \:=\mathrm{4}+\mathrm{2}\left\{\mathrm{ln}\mid\mathrm{x}\mid+\int\:\frac{\mathrm{lnx}}{\mathrm{x}}\mathrm{dx}\right\}\:\Rightarrow\:\mathrm{y}\:=−\mathrm{2}\:\overset{−} {+}\sqrt{\mathrm{ln}\mid\mathrm{x}\mid+\int\frac{\mathrm{lnx}}{\mathrm{x}}\mathrm{dx}} \\ $$
Commented by abdomathmax last updated on 27/Jul/20
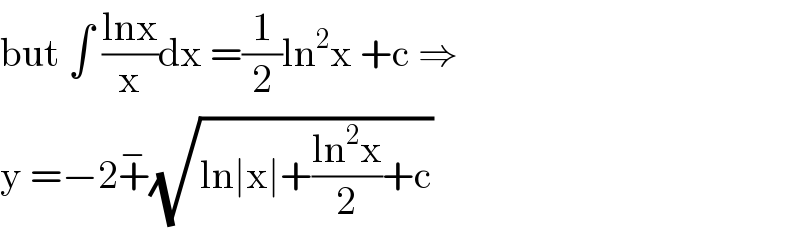
but ∫ ((lnx)/x)dx =(1/2)ln^2 x +c ⇒ y =−2+^− (√(ln∣x∣+((ln^2 x)/2)+c))
$$\mathrm{but}\:\int\:\frac{\mathrm{lnx}}{\mathrm{x}}\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \mathrm{x}\:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{y}\:=−\mathrm{2}\overset{−} {+}\sqrt{\mathrm{ln}\mid\mathrm{x}\mid+\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}{\mathrm{2}}+\mathrm{c}} \\ $$
Answered by Aziztisffola last updated on 27/Jul/20
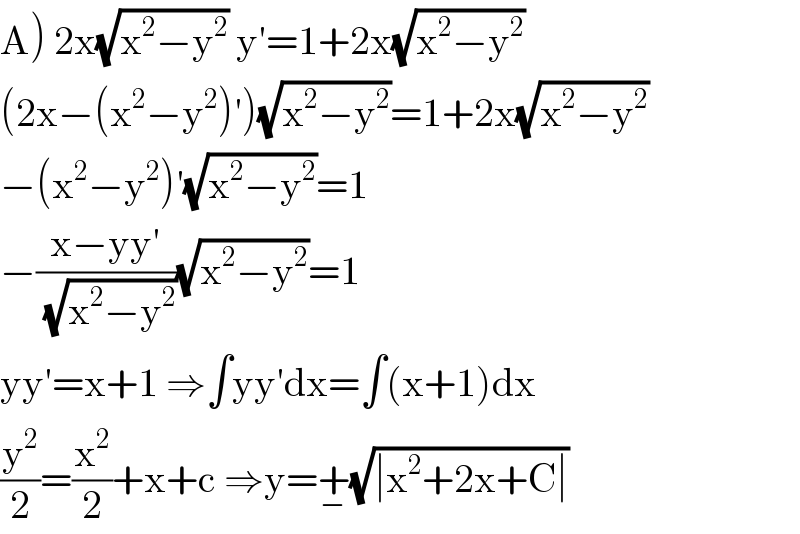
A) 2x(√(x^2 −y^2 )) y′=1+2x(√(x^2 −y^2 )) (2x−(x^2 −y^2 )′)(√(x^2 −y^2 ))=1+2x(√(x^2 −y^2 )) −(x^2 −y^2 )′(√(x^2 −y^2 ))=1 −((x−yy′)/( (√(x^2 −y^2 ))))(√(x^2 −y^2 ))=1 yy′=x+1 ⇒∫yy′dx=∫(x+1)dx (y^2 /2)=(x^2 /2)+x+c ⇒y=+_− (√(∣x^2 +2x+C∣))
$$\left.\mathrm{A}\right)\:\mathrm{2x}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }\:\mathrm{y}'=\mathrm{1}+\mathrm{2x}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} } \\ $$$$\left(\mathrm{2x}−\left(\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} \right)'\right)\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }=\mathrm{1}+\mathrm{2x}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} } \\ $$$$−\left(\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} \right)'\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }=\mathrm{1} \\ $$$$−\frac{\mathrm{x}−\mathrm{yy}'}{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\mathrm{yy}'=\mathrm{x}+\mathrm{1}\:\Rightarrow\int\mathrm{yy}'\mathrm{dx}=\int\left(\mathrm{x}+\mathrm{1}\right)\mathrm{dx} \\ $$$$\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{x}+\mathrm{c}\:\Rightarrow\mathrm{y}=\underset{−} {+}\sqrt{\mid\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{C}\mid} \\ $$
Answered by Aziztisffola last updated on 27/Jul/20
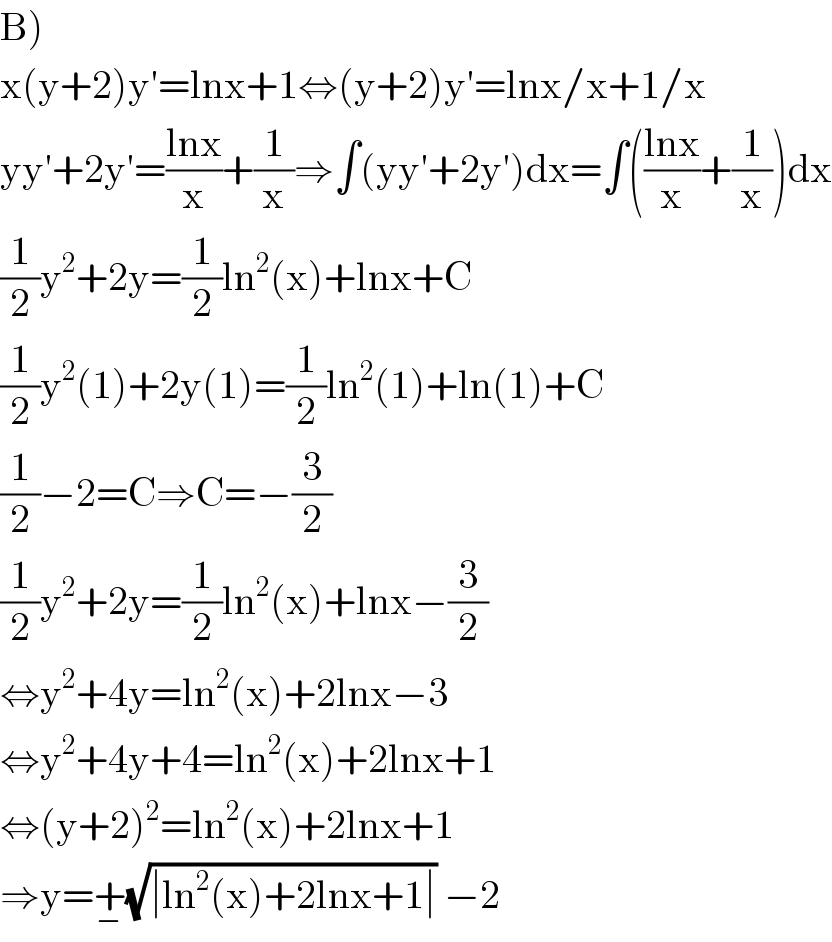
B) x(y+2)y′=lnx+1⇔(y+2)y′=lnx/x+1/x yy′+2y′=((lnx)/x)+(1/x)⇒∫(yy′+2y′)dx=∫(((lnx)/x)+(1/x))dx (1/2)y^2 +2y=(1/2)ln^2 (x)+lnx+C (1/2)y^2 (1)+2y(1)=(1/2)ln^2 (1)+ln(1)+C (1/2)−2=C⇒C=−(3/2) (1/2)y^2 +2y=(1/2)ln^2 (x)+lnx−(3/2) ⇔y^2 +4y=ln^2 (x)+2lnx−3 ⇔y^2 +4y+4=ln^2 (x)+2lnx+1 ⇔(y+2)^2 =ln^2 (x)+2lnx+1 ⇒y=+_− (√(∣ln^2 (x)+2lnx+1∣)) −2
$$\left.\mathrm{B}\right) \\ $$$$\mathrm{x}\left(\mathrm{y}+\mathrm{2}\right)\mathrm{y}'=\mathrm{lnx}+\mathrm{1}\Leftrightarrow\left(\mathrm{y}+\mathrm{2}\right)\mathrm{y}'=\mathrm{lnx}/\mathrm{x}+\mathrm{1}/\mathrm{x} \\ $$$$\mathrm{yy}'+\mathrm{2y}'=\frac{\mathrm{lnx}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{x}}\Rightarrow\int\left(\mathrm{yy}'+\mathrm{2y}'\right)\mathrm{dx}=\int\left(\frac{\mathrm{lnx}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{x}}\right)\mathrm{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{y}^{\mathrm{2}} +\mathrm{2y}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)+\mathrm{lnx}+\mathrm{C} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{y}^{\mathrm{2}} \left(\mathrm{1}\right)+\mathrm{2y}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}\right)+\mathrm{ln}\left(\mathrm{1}\right)+\mathrm{C} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}=\mathrm{C}\Rightarrow\mathrm{C}=−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{y}^{\mathrm{2}} +\mathrm{2y}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)+\mathrm{lnx}−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{y}^{\mathrm{2}} +\mathrm{4y}=\mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)+\mathrm{2lnx}−\mathrm{3} \\ $$$$\Leftrightarrow\mathrm{y}^{\mathrm{2}} +\mathrm{4y}+\mathrm{4}=\mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)+\mathrm{2lnx}+\mathrm{1} \\ $$$$\Leftrightarrow\left(\mathrm{y}+\mathrm{2}\right)^{\mathrm{2}} =\mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)+\mathrm{2lnx}+\mathrm{1} \\ $$$$\Rightarrow\mathrm{y}=\underset{−} {+}\sqrt{\mid\mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)+\mathrm{2lnx}+\mathrm{1}\mid}\:−\mathrm{2} \\ $$
Answered by abdomathmax last updated on 27/Jul/20
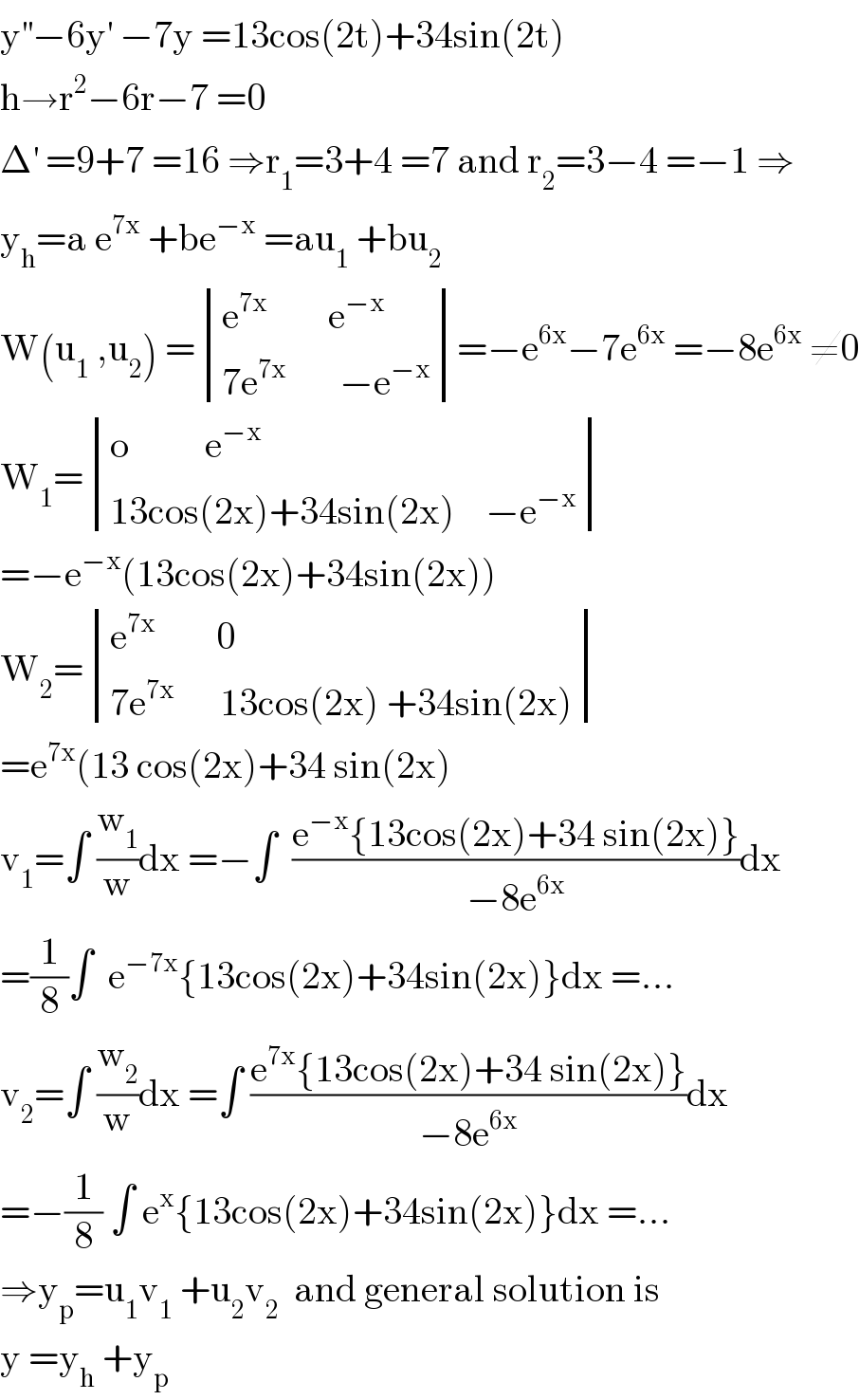
y^(′′) −6y^′ −7y =13cos(2t)+34sin(2t) h→r^2 −6r−7 =0 Δ^′ =9+7 =16 ⇒r_1 =3+4 =7 and r_2 =3−4 =−1 ⇒ y_h =a e^(7x) +be^(−x) =au_1 +bu_2 W(u_1 ,u_2 ) = determinant (((e^(7x) e^(−x) )),((7e^(7x) −e^(−x) )))=−e^(6x) −7e^(6x) =−8e^(6x) ≠0 W_1 = determinant (((o e^(−x) )),((13cos(2x)+34sin(2x) −e^(−x) ))) =−e^(−x) (13cos(2x)+34sin(2x)) W_2 = determinant (((e^(7x) 0)),((7e^(7x) 13cos(2x) +34sin(2x)))) =e^(7x) (13 cos(2x)+34 sin(2x) v_1 =∫ (w_1 /w)dx =−∫ ((e^(−x) {13cos(2x)+34 sin(2x)})/(−8e^(6x) ))dx =(1/8)∫ e^(−7x) {13cos(2x)+34sin(2x)}dx =... v_2 =∫ (w_2 /w)dx =∫ ((e^(7x) {13cos(2x)+34 sin(2x)})/(−8e^(6x) ))dx =−(1/8) ∫ e^x {13cos(2x)+34sin(2x)}dx =... ⇒y_p =u_1 v_1 +u_2 v_2 and general solution is y =y_h +y_p
$$\mathrm{y}^{''} −\mathrm{6y}^{'} \:−\mathrm{7y}\:=\mathrm{13cos}\left(\mathrm{2t}\right)+\mathrm{34sin}\left(\mathrm{2t}\right) \\ $$$$\mathrm{h}\rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{6r}−\mathrm{7}\:=\mathrm{0} \\ $$$$\Delta^{'} \:=\mathrm{9}+\mathrm{7}\:=\mathrm{16}\:\Rightarrow\mathrm{r}_{\mathrm{1}} =\mathrm{3}+\mathrm{4}\:=\mathrm{7}\:\mathrm{and}\:\mathrm{r}_{\mathrm{2}} =\mathrm{3}−\mathrm{4}\:=−\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{y}_{\mathrm{h}} =\mathrm{a}\:\mathrm{e}^{\mathrm{7x}} \:+\mathrm{be}^{−\mathrm{x}} \:=\mathrm{au}_{\mathrm{1}} \:+\mathrm{bu}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} \:,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{e}^{\mathrm{7x}} \:\:\:\:\:\:\:\:\mathrm{e}^{−\mathrm{x}} }\\{\mathrm{7e}^{\mathrm{7x}} \:\:\:\:\:\:\:−\mathrm{e}^{−\mathrm{x}} }\end{vmatrix}=−\mathrm{e}^{\mathrm{6x}} −\mathrm{7e}^{\mathrm{6x}} \:=−\mathrm{8e}^{\mathrm{6x}} \:\neq\mathrm{0} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{o}\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{−\mathrm{x}} }\\{\mathrm{13cos}\left(\mathrm{2x}\right)+\mathrm{34sin}\left(\mathrm{2x}\right)\:\:\:\:−\mathrm{e}^{−\mathrm{x}} }\end{vmatrix} \\ $$$$=−\mathrm{e}^{−\mathrm{x}} \left(\mathrm{13cos}\left(\mathrm{2x}\right)+\mathrm{34sin}\left(\mathrm{2x}\right)\right) \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{e}^{\mathrm{7x}} \:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{7e}^{\mathrm{7x}} \:\:\:\:\:\:\mathrm{13cos}\left(\mathrm{2x}\right)\:+\mathrm{34sin}\left(\mathrm{2x}\right)}\end{vmatrix} \\ $$$$=\mathrm{e}^{\mathrm{7x}} \left(\mathrm{13}\:\mathrm{cos}\left(\mathrm{2x}\right)+\mathrm{34}\:\mathrm{sin}\left(\mathrm{2x}\right)\right. \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{w}}\mathrm{dx}\:=−\int\:\:\frac{\mathrm{e}^{−\mathrm{x}} \left\{\mathrm{13cos}\left(\mathrm{2x}\right)+\mathrm{34}\:\mathrm{sin}\left(\mathrm{2x}\right)\right\}}{−\mathrm{8e}^{\mathrm{6x}} }\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int\:\:\mathrm{e}^{−\mathrm{7x}} \left\{\mathrm{13cos}\left(\mathrm{2x}\right)+\mathrm{34sin}\left(\mathrm{2x}\right)\right\}\mathrm{dx}\:=… \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{w}_{\mathrm{2}} }{\mathrm{w}}\mathrm{dx}\:=\int\:\frac{\mathrm{e}^{\mathrm{7x}} \left\{\mathrm{13cos}\left(\mathrm{2x}\right)+\mathrm{34}\:\mathrm{sin}\left(\mathrm{2x}\right)\right\}}{−\mathrm{8e}^{\mathrm{6x}} }\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{8}}\:\int\:\mathrm{e}^{\mathrm{x}} \left\{\mathrm{13cos}\left(\mathrm{2x}\right)+\mathrm{34sin}\left(\mathrm{2x}\right)\right\}\mathrm{dx}\:=… \\ $$$$\Rightarrow\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} \:\:\mathrm{and}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{is} \\ $$$$\mathrm{y}\:=\mathrm{y}_{\mathrm{h}} \:+\mathrm{y}_{\mathrm{p}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *