Menu Close

Question-105370

Tinku Tara 0 Comments
Pin




Question Number 105370 by mohammad17 last updated on 28/Jul/20
Answered by Ar Brandon last updated on 28/Jul/20
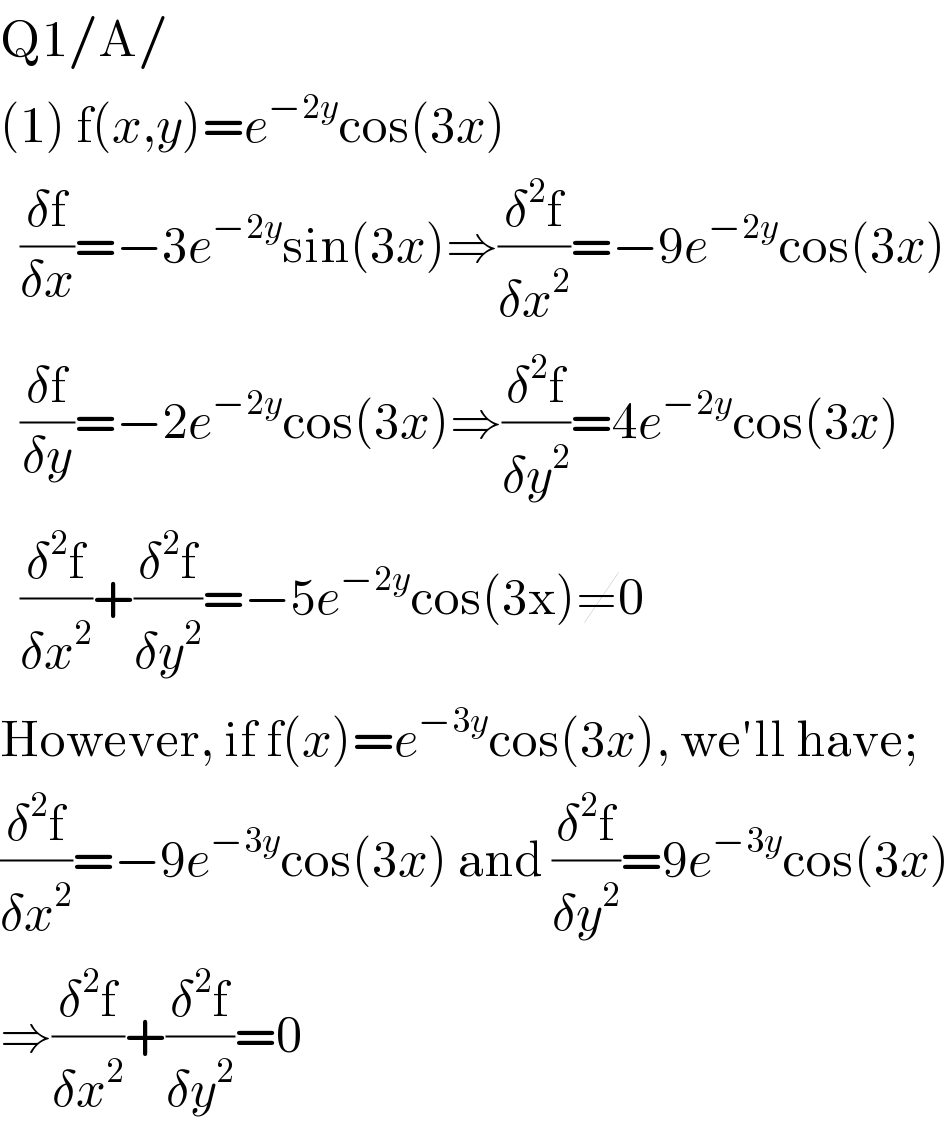
Q1/A/ (1) f(x,y)=e^(−2y) cos(3x) ((δf)/(δx))=−3e^(−2y) sin(3x)⇒((δ^2 f)/(δx^2 ))=−9e^(−2y) cos(3x) ((δf)/(δy))=−2e^(−2y) cos(3x)⇒((δ^2 f)/(δy^2 ))=4e^(−2y) cos(3x) ((δ^2 f)/(δx^2 ))+((δ^2 f)/(δy^2 ))=−5e^(−2y) cos(3x)≠0 However, if f(x)=e^(−3y) cos(3x), we′ll have; ((δ^2 f)/(δx^2 ))=−9e^(−3y) cos(3x) and ((δ^2 f)/(δy^2 ))=9e^(−3y) cos(3x) ⇒((δ^2 f)/(δx^2 ))+((δ^2 f)/(δy^2 ))=0
$$\mathrm{Q1}/\mathrm{A}/ \\ $$$$\left(\mathrm{1}\right)\:\mathrm{f}\left({x},{y}\right)={e}^{−\mathrm{2}{y}} \mathrm{cos}\left(\mathrm{3}{x}\right) \\ $$$$\:\:\frac{\delta\mathrm{f}}{\delta{x}}=−\mathrm{3}{e}^{−\mathrm{2}{y}} \mathrm{sin}\left(\mathrm{3}{x}\right)\Rightarrow\frac{\delta^{\mathrm{2}} \mathrm{f}}{\delta{x}^{\mathrm{2}} }=−\mathrm{9}{e}^{−\mathrm{2}{y}} \mathrm{cos}\left(\mathrm{3}{x}\right) \\ $$$$\:\:\frac{\delta\mathrm{f}}{\delta{y}}=−\mathrm{2}{e}^{−\mathrm{2}{y}} \mathrm{cos}\left(\mathrm{3}{x}\right)\Rightarrow\frac{\delta^{\mathrm{2}} \mathrm{f}}{\delta{y}^{\mathrm{2}} }=\mathrm{4}{e}^{−\mathrm{2}{y}} \mathrm{cos}\left(\mathrm{3}{x}\right) \\ $$$$\:\:\frac{\delta^{\mathrm{2}} \mathrm{f}}{\delta{x}^{\mathrm{2}} }+\frac{\delta^{\mathrm{2}} \mathrm{f}}{\delta{y}^{\mathrm{2}} }=−\mathrm{5}{e}^{−\mathrm{2}{y}} \mathrm{cos}\left(\mathrm{3x}\right)\neq\mathrm{0} \\ $$$$\mathrm{However},\:\mathrm{if}\:\mathrm{f}\left({x}\right)={e}^{−\mathrm{3}{y}} \mathrm{cos}\left(\mathrm{3}{x}\right),\:\mathrm{we}'\mathrm{ll}\:\mathrm{have}; \\ $$$$\frac{\delta^{\mathrm{2}} \mathrm{f}}{\delta{x}^{\mathrm{2}} }=−\mathrm{9}{e}^{−\mathrm{3}{y}} \mathrm{cos}\left(\mathrm{3}{x}\right)\:\mathrm{and}\:\frac{\delta^{\mathrm{2}} \mathrm{f}}{\delta{y}^{\mathrm{2}} }=\mathrm{9}{e}^{−\mathrm{3}{y}} \mathrm{cos}\left(\mathrm{3}{x}\right) \\ $$$$\Rightarrow\frac{\delta^{\mathrm{2}} \mathrm{f}}{\delta{x}^{\mathrm{2}} }+\frac{\delta^{\mathrm{2}} \mathrm{f}}{\delta{y}^{\mathrm{2}} }=\mathrm{0} \\ $$
Commented by mohammad17 last updated on 28/Jul/20
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Answered by Dwaipayan Shikari last updated on 28/Jul/20
∫_0 ^(log2) ∫_1 ^(log4) e^(2x+y) dydx ∫_0 ^(log2) e^(2x) [e^y ]_1 ^(log4) (4−e)∫_0 ^(log2) e^(2x) dx ((4−e)/2)[e^(2x) ]_0 ^(log2) =((4−e)/2)(4−1)=(3/2)(4−e)
$$\int_{\mathrm{0}} ^{{log}\mathrm{2}} \int_{\mathrm{1}} ^{{log}\mathrm{4}} {e}^{\mathrm{2}{x}+{y}} {dydx} \\ $$$$\int_{\mathrm{0}} ^{{log}\mathrm{2}} {e}^{\mathrm{2}{x}} \left[{e}^{{y}} \right]_{\mathrm{1}} ^{{log}\mathrm{4}} \\ $$$$\left(\mathrm{4}−{e}\right)\int_{\mathrm{0}} ^{{log}\mathrm{2}} {e}^{\mathrm{2}{x}} {dx} \\ $$$$\frac{\mathrm{4}−{e}}{\mathrm{2}}\left[{e}^{\mathrm{2}{x}} \right]_{\mathrm{0}} ^{{log}\mathrm{2}} =\frac{\mathrm{4}−{e}}{\mathrm{2}}\left(\mathrm{4}−\mathrm{1}\right)=\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{4}−{e}\right) \\ $$
Commented by mohammad17 last updated on 28/Jul/20
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Answered by Dwaipayan Shikari last updated on 28/Jul/20
∫_1 ^2 ∫_0 ^4 ((√x)/y^3 )dxdy =∫_1 ^2 (2/(3y^3 ))[x^(3/2) ]_0 ^4 dy =∫_1 ^2 ((16)/3)y^(−3) dy =−[(8/(3y^2 ))]_1 ^2 =−(2/3)+(8/3)=2
$$\int_{\mathrm{1}} ^{\mathrm{2}} \int_{\mathrm{0}} ^{\mathrm{4}} \frac{\sqrt{{x}}}{{y}^{\mathrm{3}} }{dxdy} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{2}} \frac{\mathrm{2}}{\mathrm{3}{y}^{\mathrm{3}} }\left[{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \right]_{\mathrm{0}} ^{\mathrm{4}} {dy} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{2}} \frac{\mathrm{16}}{\mathrm{3}}{y}^{−\mathrm{3}} {dy} \\ $$$$=−\left[\frac{\mathrm{8}}{\mathrm{3}{y}^{\mathrm{2}} }\right]_{\mathrm{1}} ^{\mathrm{2}} =−\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{8}}{\mathrm{3}}=\mathrm{2} \\ $$
Commented by mohammad17 last updated on 28/Jul/20
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Answered by Ar Brandon last updated on 28/Jul/20
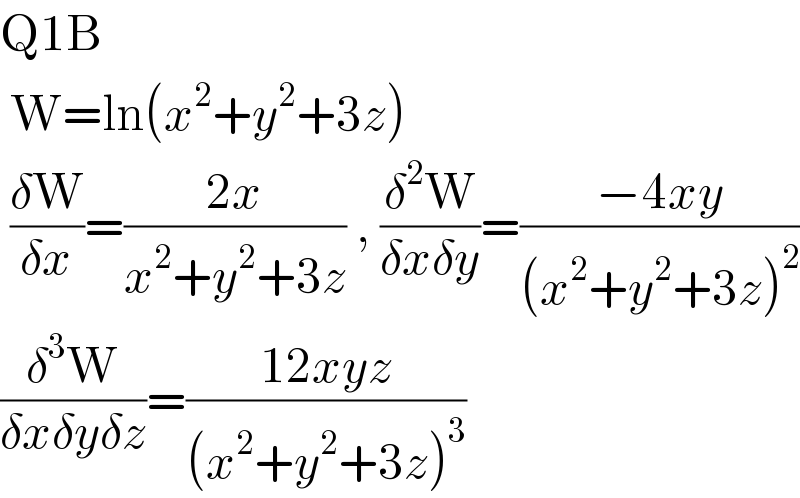
Q1B W=ln(x^2 +y^2 +3z) ((δW)/(δx))=((2x)/(x^2 +y^2 +3z)) , ((δ^2 W)/(δxδy))=((−4xy)/((x^2 +y^2 +3z)^2 )) ((δ^3 W)/(δxδyδz))=((12xyz)/((x^2 +y^2 +3z)^3 ))
$$\mathrm{Q1B} \\ $$$$\:\mathrm{W}=\mathrm{ln}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{3}{z}\right) \\ $$$$\:\frac{\delta\mathrm{W}}{\delta{x}}=\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{3}{z}}\:,\:\frac{\delta^{\mathrm{2}} \mathrm{W}}{\delta{x}\delta{y}}=\frac{−\mathrm{4}{xy}}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{3}{z}\right)^{\mathrm{2}} } \\ $$$$\frac{\delta^{\mathrm{3}} \mathrm{W}}{\delta{x}\delta{y}\delta{z}}=\frac{\mathrm{12}{xyz}}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{3}{z}\right)^{\mathrm{3}} } \\ $$
Commented by mohammad17 last updated on 28/Jul/20
thank you sir
$${thank}\:{you}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *