Question-105380

Question Number 105380 by Skabetix last updated on 28/Jul/20

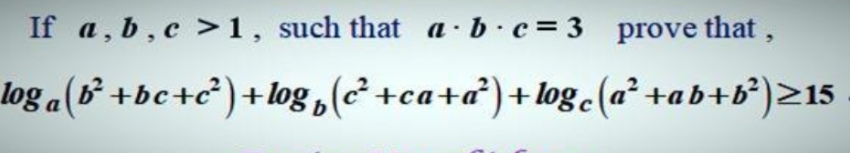
Commented by Skabetix last updated on 28/Jul/20

$${pls}\:{need}\:{help} \\ $$

Answered by 1549442205PVT last updated on 28/Jul/20

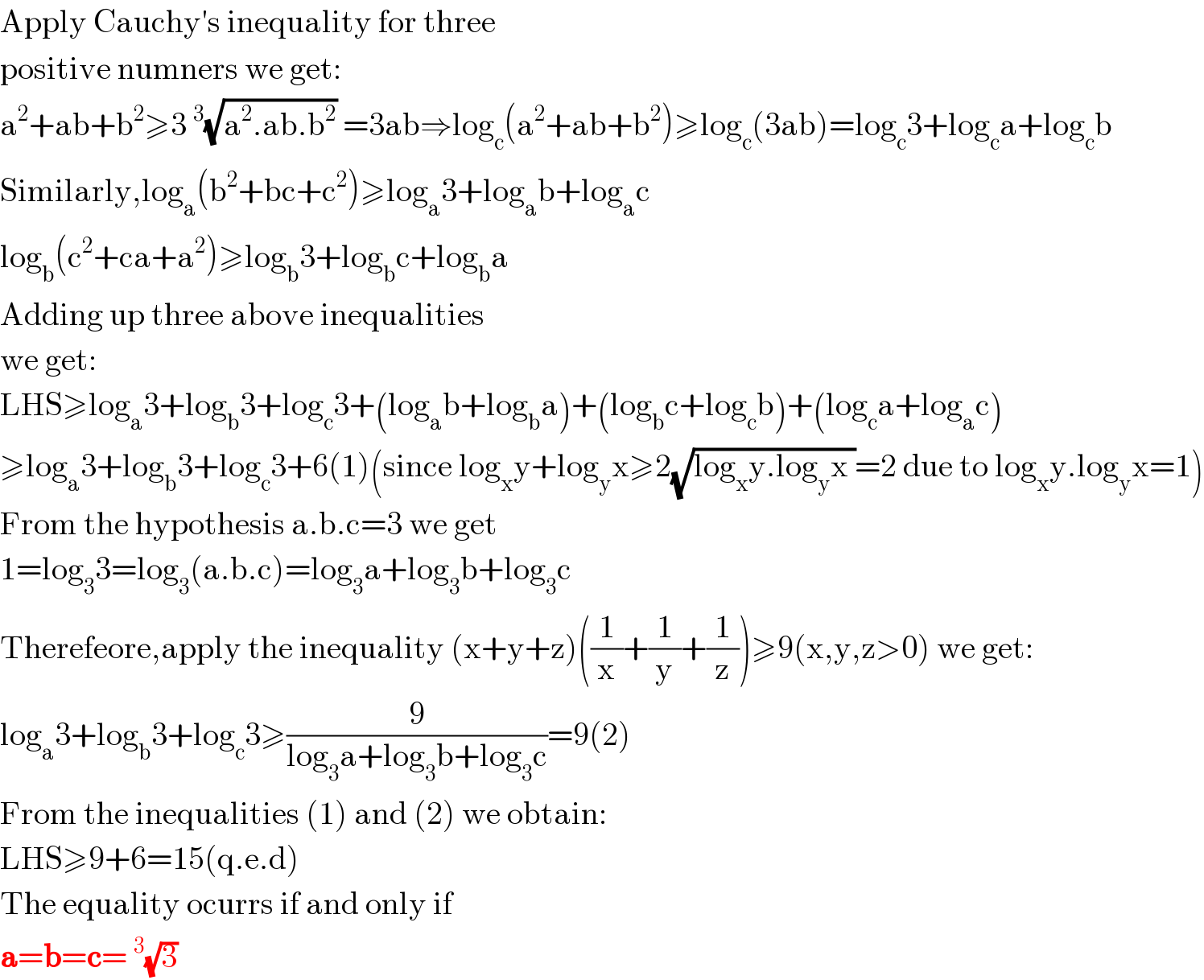
Apply Cauchy′s inequality for three positive numners we get: a^2 +ab+b^2 ≥3^3 (√(a^2 .ab.b^2 )) =3ab⇒log_c (a^2 +ab+b^2 )≥log_c (3ab)=log_c 3+log_c a+log_c b Similarly,log_a (b^2 +bc+c^2 )≥log_a 3+log_a b+log_a c log_b (c^2 +ca+a^2 )≥log_b 3+log_b c+log_b a Adding up three above inequalities we get: LHS≥log_a 3+log_b 3+log_c 3+(log_a b+log_b a)+(log_b c+log_c b)+(log_c a+log_a c) ≥log_a 3+log_b 3+log_c 3+6(1)(since log_x y+log_y x≥2(√(log_x y.log_y x ))=2 due to log_x y.log_y x=1) From the hypothesis a.b.c=3 we get 1=log_3 3=log_3 (a.b.c)=log_3 a+log_3 b+log_3 c Therefeore,apply the inequality (x+y+z)((1/x)+(1/y)+(1/z))≥9(x,y,z>0) we get: log_a 3+log_b 3+log_c 3≥(9/(log_3 a+log_3 b+log_3 c))=9(2) From the inequalities (1) and (2) we obtain: LHS≥9+6=15(q.e.d) The equality ocurrs if and only if a=b=c=^3 (√3)

$$\mathrm{Apply}\:\mathrm{Cauchy}'\mathrm{s}\:\mathrm{inequality}\:\mathrm{for}\:\mathrm{three} \\ $$$$\mathrm{positive}\:\mathrm{numners}\:\mathrm{we}\:\mathrm{get}: \\ $$$$\mathrm{a}^{\mathrm{2}} +\mathrm{ab}+\mathrm{b}^{\mathrm{2}} \geqslant\mathrm{3}\:^{\mathrm{3}} \sqrt{\mathrm{a}^{\mathrm{2}} .\mathrm{ab}.\mathrm{b}^{\mathrm{2}} }\:=\mathrm{3ab}\Rightarrow\mathrm{log}_{\mathrm{c}} \left(\mathrm{a}^{\mathrm{2}} +\mathrm{ab}+\mathrm{b}^{\mathrm{2}} \right)\geqslant\mathrm{log}_{\mathrm{c}} \left(\mathrm{3ab}\right)=\mathrm{log}_{\mathrm{c}} \mathrm{3}+\mathrm{log}_{\mathrm{c}} \mathrm{a}+\mathrm{log}_{\mathrm{c}} \mathrm{b} \\ $$$$\mathrm{Similarly},\mathrm{log}_{\mathrm{a}} \left(\mathrm{b}^{\mathrm{2}} +\mathrm{bc}+\mathrm{c}^{\mathrm{2}} \right)\geqslant\mathrm{log}_{\mathrm{a}} \mathrm{3}+\mathrm{log}_{\mathrm{a}} \mathrm{b}+\mathrm{log}_{\mathrm{a}} \mathrm{c} \\ $$$$\mathrm{log}_{\mathrm{b}} \left(\mathrm{c}^{\mathrm{2}} +\mathrm{ca}+\mathrm{a}^{\mathrm{2}} \right)\geqslant\mathrm{log}_{\mathrm{b}} \mathrm{3}+\mathrm{log}_{\mathrm{b}} \mathrm{c}+\mathrm{log}_{\mathrm{b}} \mathrm{a} \\ $$$$\mathrm{Adding}\:\mathrm{up}\:\mathrm{three}\:\mathrm{above}\:\mathrm{inequalities} \\ $$$$\mathrm{we}\:\mathrm{get}: \\ $$$$\mathrm{LHS}\geqslant\mathrm{log}_{\mathrm{a}} \mathrm{3}+\mathrm{log}_{\mathrm{b}} \mathrm{3}+\mathrm{log}_{\mathrm{c}} \mathrm{3}+\left(\mathrm{log}_{\mathrm{a}} \mathrm{b}+\mathrm{log}_{\mathrm{b}} \mathrm{a}\right)+\left(\mathrm{log}_{\mathrm{b}} \mathrm{c}+\mathrm{log}_{\mathrm{c}} \mathrm{b}\right)+\left(\mathrm{log}_{\mathrm{c}} \mathrm{a}+\mathrm{log}_{\mathrm{a}} \mathrm{c}\right) \\ $$$$\geqslant\mathrm{log}_{\mathrm{a}} \mathrm{3}+\mathrm{log}_{\mathrm{b}} \mathrm{3}+\mathrm{log}_{\mathrm{c}} \mathrm{3}+\mathrm{6}\left(\mathrm{1}\right)\left(\mathrm{since}\:\mathrm{log}_{\mathrm{x}} \mathrm{y}+\mathrm{log}_{\mathrm{y}} \mathrm{x}\geqslant\mathrm{2}\sqrt{\mathrm{log}_{\mathrm{x}} \mathrm{y}.\mathrm{log}_{\mathrm{y}} \mathrm{x}\:}=\mathrm{2}\:\mathrm{due}\:\mathrm{to}\:\mathrm{log}_{\mathrm{x}} \mathrm{y}.\mathrm{log}_{\mathrm{y}} \mathrm{x}=\mathrm{1}\right) \\ $$$$\mathrm{From}\:\mathrm{the}\:\mathrm{hypothesis}\:\mathrm{a}.\mathrm{b}.\mathrm{c}=\mathrm{3}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{1}=\mathrm{log}_{\mathrm{3}} \mathrm{3}=\mathrm{log}_{\mathrm{3}} \left(\mathrm{a}.\mathrm{b}.\mathrm{c}\right)=\mathrm{log}_{\mathrm{3}} \mathrm{a}+\mathrm{log}_{\mathrm{3}} \mathrm{b}+\mathrm{log}_{\mathrm{3}} \mathrm{c} \\ $$$$\mathrm{Therefeore},\mathrm{apply}\:\mathrm{the}\:\mathrm{inequality}\:\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)\left(\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{y}}+\frac{\mathrm{1}}{\mathrm{z}}\right)\geqslant\mathrm{9}\left(\mathrm{x},\mathrm{y},\mathrm{z}>\mathrm{0}\right)\:\mathrm{we}\:\mathrm{get}: \\ $$$$\mathrm{log}_{\mathrm{a}} \mathrm{3}+\mathrm{log}_{\mathrm{b}} \mathrm{3}+\mathrm{log}_{\mathrm{c}} \mathrm{3}\geqslant\frac{\mathrm{9}}{\mathrm{log}_{\mathrm{3}} \mathrm{a}+\mathrm{log}_{\mathrm{3}} \mathrm{b}+\mathrm{log}_{\mathrm{3}} \mathrm{c}}=\mathrm{9}\left(\mathrm{2}\right) \\ $$$$\mathrm{From}\:\mathrm{the}\:\mathrm{inequalities}\:\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{2}\right)\:\mathrm{we}\:\mathrm{obtain}: \\ $$$$\mathrm{LHS}\geqslant\mathrm{9}+\mathrm{6}=\mathrm{15}\left(\mathrm{q}.\mathrm{e}.\mathrm{d}\right) \\ $$$$\mathrm{The}\:\mathrm{equality}\:\mathrm{ocurrs}\:\mathrm{if}\:\mathrm{and}\:\mathrm{only}\:\mathrm{if} \\ $$$$\boldsymbol{\mathrm{a}}=\boldsymbol{\mathrm{b}}=\boldsymbol{\mathrm{c}}=\:^{\mathrm{3}} \sqrt{\mathrm{3}}\: \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply