Question Number 105388 by mohammad17 last updated on 28/Jul/20

Answered by john santu last updated on 28/Jul/20
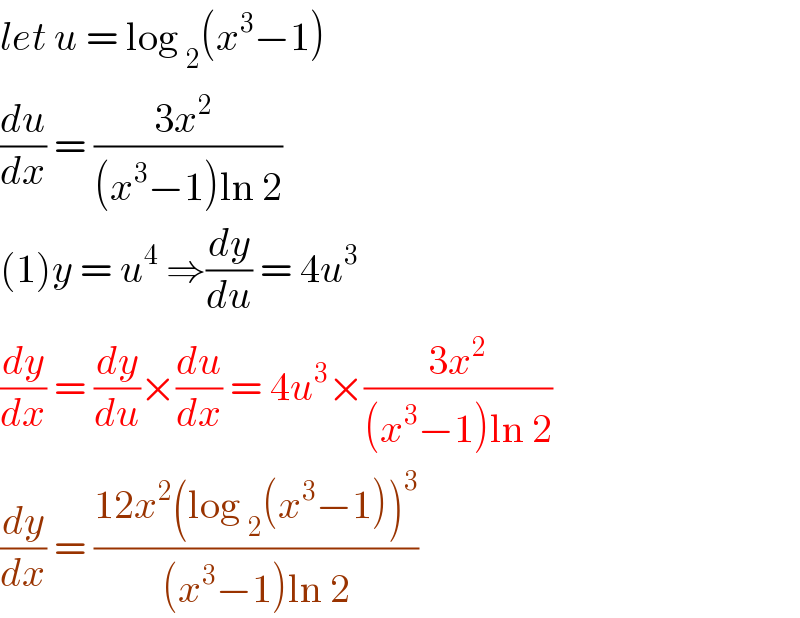
$${let}\:{u}\:=\:\mathrm{log}\:_{\mathrm{2}} \left({x}^{\mathrm{3}} −\mathrm{1}\right) \\ $$$$\frac{{du}}{{dx}}\:=\:\frac{\mathrm{3}{x}^{\mathrm{2}} \:}{\left({x}^{\mathrm{3}} −\mathrm{1}\right)\mathrm{ln}\:\mathrm{2}} \\ $$$$\left(\mathrm{1}\right){y}\:=\:{u}^{\mathrm{4}} \:\Rightarrow\frac{{dy}}{{du}}\:=\:\mathrm{4}{u}^{\mathrm{3}} \\ $$$$\frac{{dy}}{{dx}}\:=\:\frac{{dy}}{{du}}×\frac{{du}}{{dx}}\:=\:\mathrm{4}{u}^{\mathrm{3}} ×\frac{\mathrm{3}{x}^{\mathrm{2}} }{\left({x}^{\mathrm{3}} −\mathrm{1}\right)\mathrm{ln}\:\mathrm{2}} \\ $$$$\frac{{dy}}{{dx}}\:=\:\frac{\mathrm{12}{x}^{\mathrm{2}} \left(\mathrm{log}\:_{\mathrm{2}} \left({x}^{\mathrm{3}} −\mathrm{1}\right)\right)^{\mathrm{3}} }{\left({x}^{\mathrm{3}} −\mathrm{1}\right)\mathrm{ln}\:\mathrm{2}} \\ $$
Answered by Dwaipayan Shikari last updated on 28/Jul/20
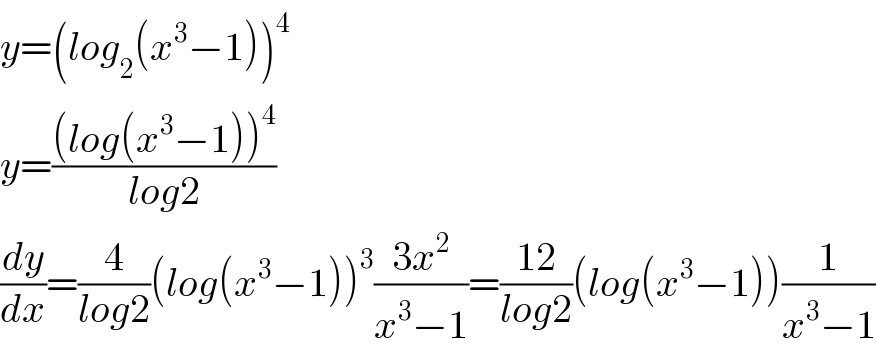
$${y}=\left({log}_{\mathrm{2}} \left({x}^{\mathrm{3}} −\mathrm{1}\right)\right)^{\mathrm{4}} \\ $$$${y}=\frac{\left({log}\left({x}^{\mathrm{3}} −\mathrm{1}\right)\right)^{\mathrm{4}} }{{log}\mathrm{2}} \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{4}}{{log}\mathrm{2}}\left({log}\left({x}^{\mathrm{3}} −\mathrm{1}\right)\right)^{\mathrm{3}} \frac{\mathrm{3}{x}^{\mathrm{2}} }{{x}^{\mathrm{3}} −\mathrm{1}}=\frac{\mathrm{12}}{{log}\mathrm{2}}\left({log}\left({x}^{\mathrm{3}} −\mathrm{1}\right)\right)\frac{\mathrm{1}}{{x}^{\mathrm{3}} −\mathrm{1}} \\ $$
Answered by mathmax by abdo last updated on 28/Jul/20
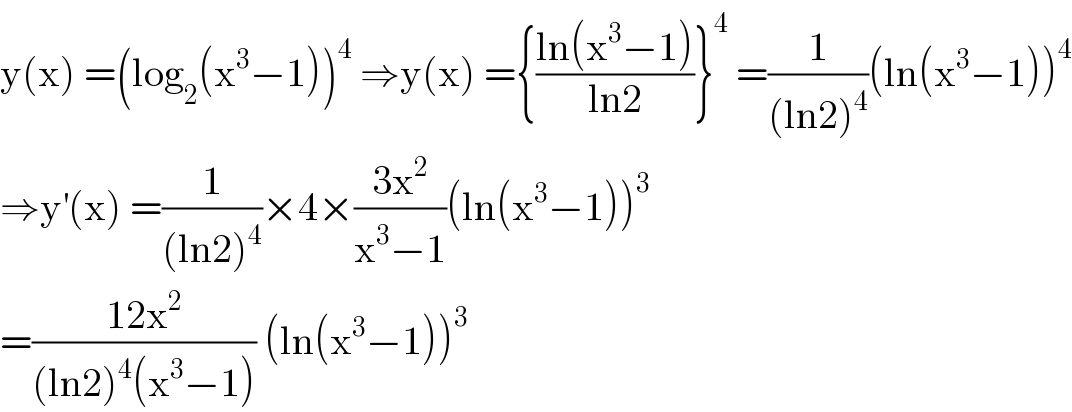
$$\mathrm{y}\left(\mathrm{x}\right)\:=\left(\mathrm{log}_{\mathrm{2}} \left(\mathrm{x}^{\mathrm{3}} −\mathrm{1}\right)\right)^{\mathrm{4}} \:\Rightarrow\mathrm{y}\left(\mathrm{x}\right)\:=\left\{\frac{\mathrm{ln}\left(\mathrm{x}^{\mathrm{3}} −\mathrm{1}\right)}{\mathrm{ln2}}\right\}^{\mathrm{4}} \:=\frac{\mathrm{1}}{\left(\mathrm{ln2}\right)^{\mathrm{4}} }\left(\mathrm{ln}\left(\mathrm{x}^{\mathrm{3}} −\mathrm{1}\right)\right)^{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{y}^{'} \left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{ln2}\right)^{\mathrm{4}} }×\mathrm{4}×\frac{\mathrm{3x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{3}} −\mathrm{1}}\left(\mathrm{ln}\left(\mathrm{x}^{\mathrm{3}} −\mathrm{1}\right)\right)^{\mathrm{3}} \\ $$$$=\frac{\mathrm{12x}^{\mathrm{2}} }{\left(\mathrm{ln2}\right)^{\mathrm{4}} \left(\mathrm{x}^{\mathrm{3}} −\mathrm{1}\right)}\:\left(\mathrm{ln}\left(\mathrm{x}^{\mathrm{3}} −\mathrm{1}\right)\right)^{\mathrm{3}} \\ $$
