Question Number 105476 by ajfour last updated on 29/Jul/20

Commented by ajfour last updated on 29/Jul/20
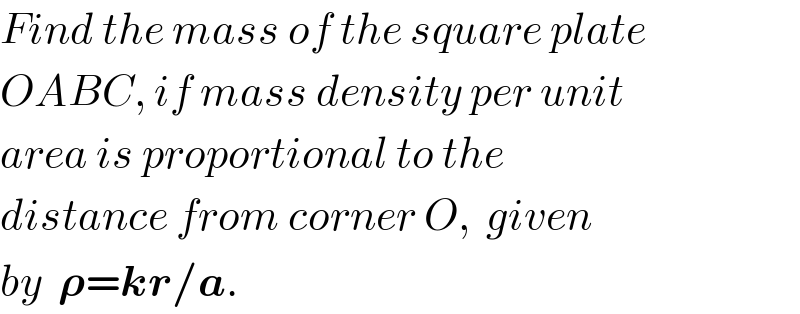
$${Find}\:{the}\:{mass}\:{of}\:{the}\:{square}\:{plate} \\ $$$${OABC},\:{if}\:{mass}\:{density}\:{per}\:{unit} \\ $$$${area}\:{is}\:{proportional}\:{to}\:{the} \\ $$$${distance}\:{from}\:{corner}\:{O},\:\:{given} \\ $$$${by}\:\:\boldsymbol{\rho}=\boldsymbol{{kr}}/\boldsymbol{{a}}. \\ $$
Answered by mr W last updated on 29/Jul/20
![M=2∫_0 ^(π/4) ∫_0 ^(a/(cos θ)) ρrdrdθ =((2k)/a)∫_0 ^(π/4) ∫_0 ^(a/(cos θ)) r^2 drdθ =((2a^2 k)/3)∫_0 ^(π/4) (dθ/(cos^3 θ)) =((2a^2 k)/3)∫_0 ^(π/4) ((d(sin θ))/((1−sin^2 θ)^2 )) =((a^2 k)/6)[ln ((1+sin θ)/(1−sin θ))−(1/(1+sin θ))+(1/(1−sin θ))]_0 ^(π/4) =((a^2 k)/6)[ln ((1+(1/( (√2))))/(1−(1/( (√2)))))−(1/(1+(1/( (√2)))))+(1/(1−(1/( (√2)))))] =((a^2 k)/3)[ln ((√2)+1)+(√2)]](https://www.tinkutara.com/question/Q105494.png)
$${M}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \int_{\mathrm{0}} ^{\frac{{a}}{\mathrm{cos}\:\theta}} \rho{rdrd}\theta \\ $$$$=\frac{\mathrm{2}{k}}{{a}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \int_{\mathrm{0}} ^{\frac{{a}}{\mathrm{cos}\:\theta}} {r}^{\mathrm{2}} {drd}\theta \\ $$$$=\frac{\mathrm{2}{a}^{\mathrm{2}} {k}}{\mathrm{3}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{d}\theta}{\mathrm{cos}^{\mathrm{3}} \:\theta} \\ $$$$=\frac{\mathrm{2}{a}^{\mathrm{2}} {k}}{\mathrm{3}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{d}\left(\mathrm{sin}\:\theta\right)}{\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} } \\ $$$$=\frac{{a}^{\mathrm{2}} {k}}{\mathrm{6}}\left[\mathrm{ln}\:\frac{\mathrm{1}+\mathrm{sin}\:\theta}{\mathrm{1}−\mathrm{sin}\:\theta}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{sin}\:\theta}+\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}\:\theta}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$=\frac{{a}^{\mathrm{2}} {k}}{\mathrm{6}}\left[\mathrm{ln}\:\frac{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}−\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}+\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}\right] \\ $$$$=\frac{{a}^{\mathrm{2}} {k}}{\mathrm{3}}\left[\mathrm{ln}\:\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)+\sqrt{\mathrm{2}}\right] \\ $$
Commented by ajfour last updated on 29/Jul/20
$${Fantastic},\:{Sir}.\:{Thanks}\:{a}\:{lot}. \\ $$
