Question-105536

Question Number 105536 by I want to learn more last updated on 29/Jul/20

Answered by adhigenz last updated on 29/Jul/20

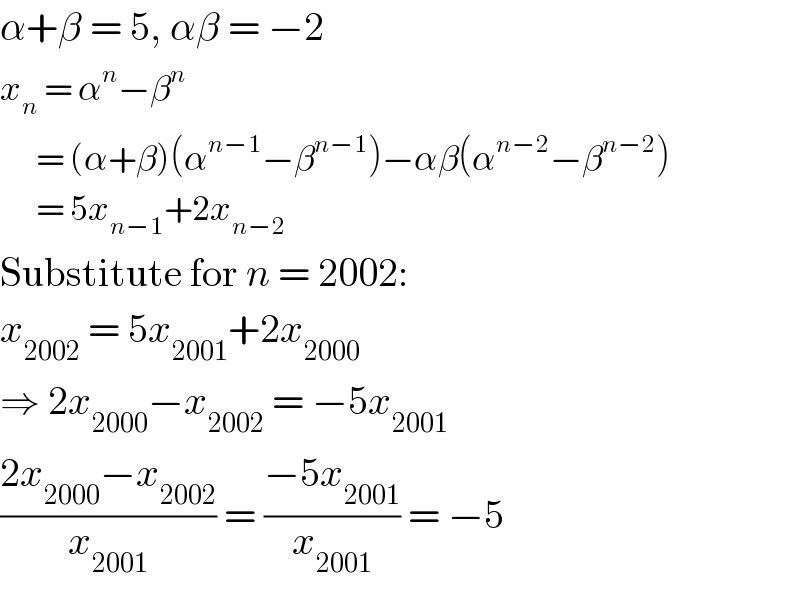
α+β = 5, αβ = −2 x_n = α^n −β^n = (α+β)(α^(n−1) −β^(n−1) )−αβ(α^(n−2) −β^(n−2) ) = 5x_(n−1) +2x_(n−2) Substitute for n = 2002: x_(2002) = 5x_(2001) +2x_(2000) ⇒ 2x_(2000) −x_(2002) = −5x_(2001) ((2x_(2000) −x_(2002) )/x_(2001) ) = ((−5x_(2001) )/x_(2001) ) = −5

$$\alpha+\beta\:=\:\mathrm{5},\:\alpha\beta\:=\:−\mathrm{2} \\ $$$${x}_{{n}} \:=\:\alpha^{{n}} −\beta^{{n}} \\ $$$$\:\:\:\:\:\:=\:\left(\alpha+\beta\right)\left(\alpha^{{n}−\mathrm{1}} −\beta^{{n}−\mathrm{1}} \right)−\alpha\beta\left(\alpha^{{n}−\mathrm{2}} −\beta^{{n}−\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:=\:\mathrm{5}{x}_{{n}−\mathrm{1}} +\mathrm{2}{x}_{{n}−\mathrm{2}} \\ $$$$\mathrm{Substitute}\:\mathrm{for}\:{n}\:=\:\mathrm{2002}: \\ $$$${x}_{\mathrm{2002}} \:=\:\mathrm{5}{x}_{\mathrm{2001}} +\mathrm{2}{x}_{\mathrm{2000}} \\ $$$$\Rightarrow\:\mathrm{2}{x}_{\mathrm{2000}} −{x}_{\mathrm{2002}} \:=\:−\mathrm{5}{x}_{\mathrm{2001}} \\ $$$$\frac{\mathrm{2}{x}_{\mathrm{2000}} −{x}_{\mathrm{2002}} }{{x}_{\mathrm{2001}} }\:=\:\frac{−\mathrm{5}{x}_{\mathrm{2001}} }{{x}_{\mathrm{2001}} }\:=\:−\mathrm{5} \\ $$

Commented by I want to learn more last updated on 29/Jul/20

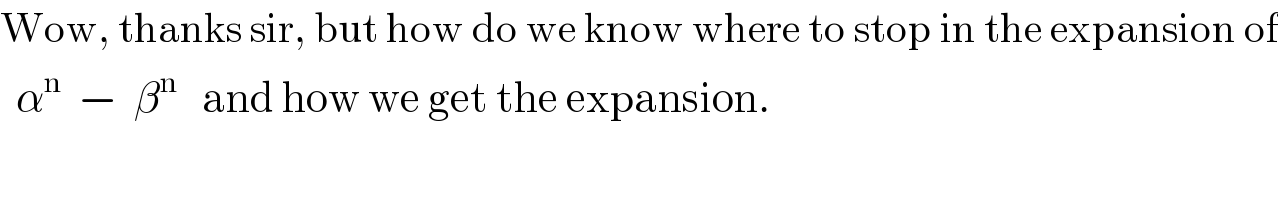
Wow, thanks sir, but how do we know where to stop in the expansion of α^n − β^n and how we get the expansion.

$$\mathrm{Wow},\:\mathrm{thanks}\:\mathrm{sir},\:\mathrm{but}\:\mathrm{how}\:\mathrm{do}\:\mathrm{we}\:\mathrm{know}\:\mathrm{where}\:\mathrm{to}\:\mathrm{stop}\:\mathrm{in}\:\mathrm{the}\:\mathrm{expansion}\:\mathrm{of} \\ $$$$\:\:\alpha^{\mathrm{n}} \:\:−\:\:\beta^{\mathrm{n}} \:\:\:\mathrm{and}\:\mathrm{how}\:\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{expansion}. \\ $$

Commented by adhigenz last updated on 30/Jul/20

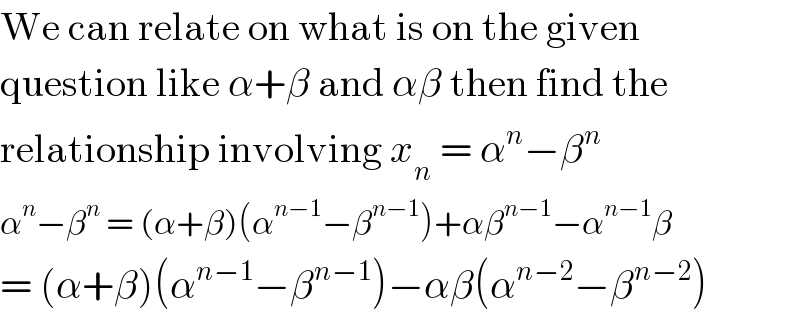
We can relate on what is on the given question like α+β and αβ then find the relationship involving x_n = α^n −β^n α^n −β^n = (α+β)(α^(n−1) −β^(n−1) )+αβ^(n−1) −α^(n−1) β = (α+β)(α^(n−1) −β^(n−1) )−αβ(α^(n−2) −β^(n−2) )

$$\mathrm{We}\:\mathrm{can}\:\mathrm{relate}\:\mathrm{on}\:\mathrm{what}\:\mathrm{is}\:\mathrm{on}\:\mathrm{the}\:\mathrm{given} \\ $$$$\mathrm{question}\:\mathrm{like}\:\alpha+\beta\:\mathrm{and}\:\alpha\beta\:\mathrm{then}\:\mathrm{find}\:\mathrm{the} \\ $$$$\mathrm{relationship}\:\mathrm{involving}\:{x}_{{n}} \:=\:\alpha^{{n}} −\beta^{{n}} \\ $$$$\alpha^{{n}} −\beta^{{n}} \:=\:\left(\alpha+\beta\right)\left(\alpha^{{n}−\mathrm{1}} −\beta^{{n}−\mathrm{1}} \right)+\alpha\beta^{{n}−\mathrm{1}} −\alpha^{{n}−\mathrm{1}} \beta \\ $$$$=\:\left(\alpha+\beta\right)\left(\alpha^{{n}−\mathrm{1}} −\beta^{{n}−\mathrm{1}} \right)−\alpha\beta\left(\alpha^{{n}−\mathrm{2}} −\beta^{{n}−\mathrm{2}} \right) \\ $$

Commented by I want to learn more last updated on 30/Jul/20

$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply