Question Number 105599 by mohammad17 last updated on 30/Jul/20

Answered by bobhans last updated on 30/Jul/20
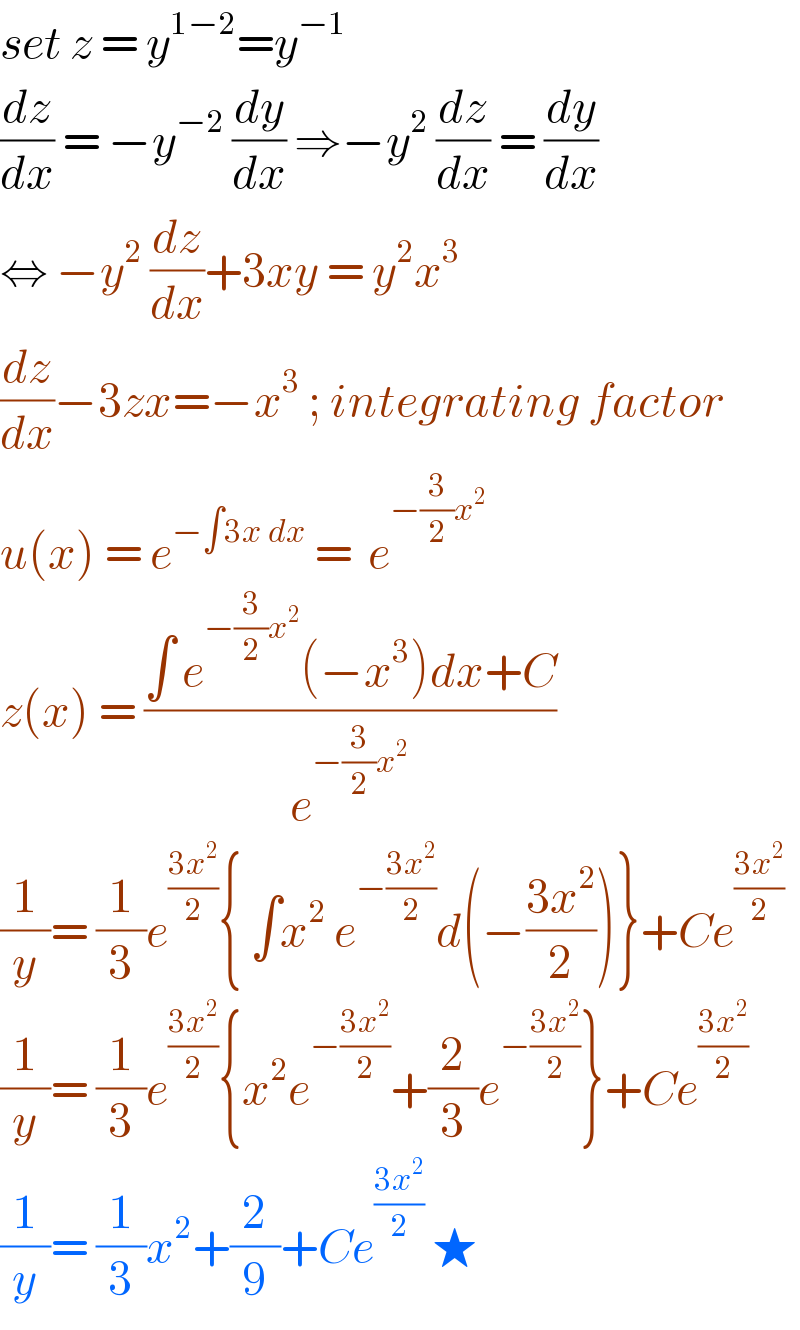
$${set}\:{z}\:=\:{y}^{\mathrm{1}−\mathrm{2}} ={y}^{−\mathrm{1}} \\ $$$$\frac{{dz}}{{dx}}\:=\:−{y}^{−\mathrm{2}} \:\frac{{dy}}{{dx}}\:\Rightarrow−{y}^{\mathrm{2}} \:\frac{{dz}}{{dx}}\:=\:\frac{{dy}}{{dx}}\: \\ $$$$\Leftrightarrow\:−{y}^{\mathrm{2}} \:\frac{{dz}}{{dx}}+\mathrm{3}{xy}\:=\:{y}^{\mathrm{2}} {x}^{\mathrm{3}} \\ $$$$\frac{{dz}}{{dx}}−\mathrm{3}{zx}=−{x}^{\mathrm{3}} \:;\:{integrating}\:{factor} \\ $$$${u}\left({x}\right)\:=\:{e}^{−\int\mathrm{3}{x}\:{dx}} \:=\:\:{e}^{−\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} } \\ $$$${z}\left({x}\right)\:=\:\frac{\int\:{e}^{−\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} } \left(−{x}^{\mathrm{3}} \right){dx}+{C}}{{e}^{−\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} } }\: \\ $$$$\frac{\mathrm{1}}{{y}}=\:\frac{\mathrm{1}}{\mathrm{3}}{e}^{\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}}} \left\{\:\int{x}^{\mathrm{2}} \:{e}^{−\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}}} {d}\left(−\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}}\right)\right\}+{Ce}^{\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$$\frac{\mathrm{1}}{{y}}=\:\frac{\mathrm{1}}{\mathrm{3}}{e}^{\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}}} \left\{{x}^{\mathrm{2}} {e}^{−\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}}} +\frac{\mathrm{2}}{\mathrm{3}}{e}^{−\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}}} \right\}+{Ce}^{\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$$\frac{\mathrm{1}}{{y}}=\:\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{2}} +\frac{\mathrm{2}}{\mathrm{9}}+{Ce}^{\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}}} \:\bigstar \\ $$
