Question-105673

Question Number 105673 by I want to learn more last updated on 30/Jul/20

Answered by mathmax by abdo last updated on 30/Jul/20

A =Σ_(k=1) ^(15) f(k) =Σ_(k=1) ^(15) arctan((1/(k^2 +k+1))) =Σ_(k=1) ^(15) arctan(((k+1−k)/(1+k(k+1)))) let k =tanu_k ⇒((k+1−k)/(1+k(k+1))) =((tan(u_(k+1) )−tanu_k )/(1+tan(u_k )tanu_(k+1) )) =tan(u_(k+1) −u_k ) ⇒arctan(((k+1−k)/(1+k(k+1)))) =u_(k+1) −u_k ⇒A =Σ_(k=1) ^(15) (u_(k+1) −u_k ) =u_2 −u_1 +u_3 −u_2 +....+u_(16) −u_(15) =u_(16) −u_1 =arctan(16)−arctan(1) =arctan(16)−arctan(1) ⇒ tanA =tan(arctan(16)−ar4tan(1)) =((16−1)/(1+16×1)) =((15)/(17)) the answer is b

$$\mathrm{A}\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{15}} \mathrm{f}\left(\mathrm{k}\right)\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{15}} \:\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} +\mathrm{k}+\mathrm{1}}\right)\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{15}} \:\mathrm{arctan}\left(\frac{\mathrm{k}+\mathrm{1}−\mathrm{k}}{\mathrm{1}+\mathrm{k}\left(\mathrm{k}+\mathrm{1}\right)}\right) \\ $$$$\mathrm{let}\:\mathrm{k}\:=\mathrm{tanu}_{\mathrm{k}} \:\Rightarrow\frac{\mathrm{k}+\mathrm{1}−\mathrm{k}}{\mathrm{1}+\mathrm{k}\left(\mathrm{k}+\mathrm{1}\right)}\:=\frac{\mathrm{tan}\left(\mathrm{u}_{\mathrm{k}+\mathrm{1}} \right)−\mathrm{tanu}_{\mathrm{k}} }{\mathrm{1}+\mathrm{tan}\left(\mathrm{u}_{\mathrm{k}} \right)\mathrm{tanu}_{\mathrm{k}+\mathrm{1}} }\:=\mathrm{tan}\left(\mathrm{u}_{\mathrm{k}+\mathrm{1}} −\mathrm{u}_{\mathrm{k}} \right) \\ $$$$\Rightarrow\mathrm{arctan}\left(\frac{\mathrm{k}+\mathrm{1}−\mathrm{k}}{\mathrm{1}+\mathrm{k}\left(\mathrm{k}+\mathrm{1}\right)}\right)\:=\mathrm{u}_{\mathrm{k}+\mathrm{1}} −\mathrm{u}_{\mathrm{k}} \:\Rightarrow\mathrm{A}\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{15}} \left(\mathrm{u}_{\mathrm{k}+\mathrm{1}} −\mathrm{u}_{\mathrm{k}} \right) \\ $$$$=\mathrm{u}_{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{3}} −\mathrm{u}_{\mathrm{2}} \:+….+\mathrm{u}_{\mathrm{16}} −\mathrm{u}_{\mathrm{15}} =\mathrm{u}_{\mathrm{16}} −\mathrm{u}_{\mathrm{1}} =\mathrm{arctan}\left(\mathrm{16}\right)−\mathrm{arctan}\left(\mathrm{1}\right) \\ $$$$=\mathrm{arctan}\left(\mathrm{16}\right)−\mathrm{arctan}\left(\mathrm{1}\right)\:\Rightarrow \\ $$$$\mathrm{tanA}\:=\mathrm{tan}\left(\mathrm{arctan}\left(\mathrm{16}\right)−\mathrm{ar4tan}\left(\mathrm{1}\right)\right)\:=\frac{\mathrm{16}−\mathrm{1}}{\mathrm{1}+\mathrm{16}×\mathrm{1}}\:=\frac{\mathrm{15}}{\mathrm{17}} \\ $$$$\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{b} \\ $$

Commented by I want to learn more last updated on 31/Jul/20

$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate}. \\ $$

Commented by abdomsup last updated on 31/Jul/20

$${you}\:{are}\:{welcome} \\ $$

Answered by Dwaipayan Shikari last updated on 31/Jul/20

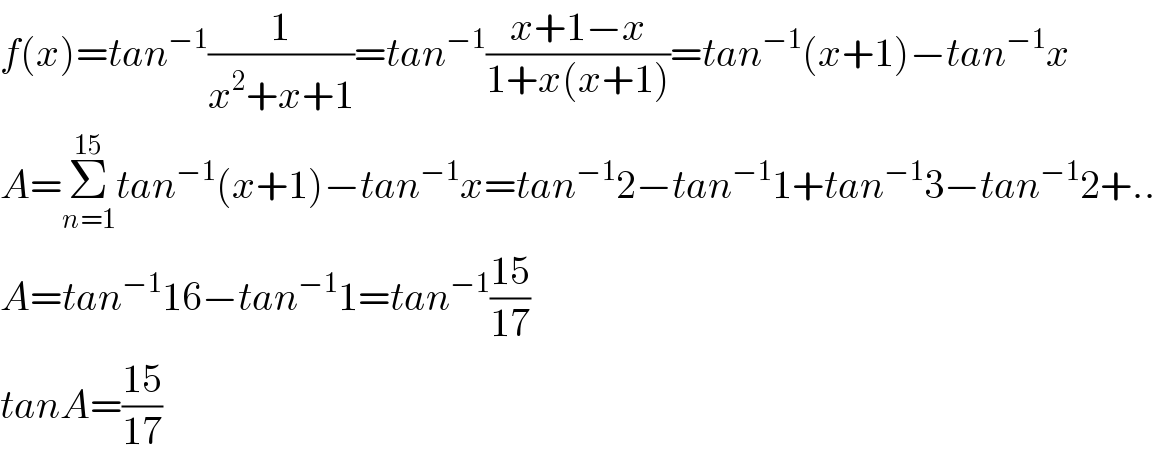
f(x)=tan^(−1) (1/(x^2 +x+1))=tan^(−1) ((x+1−x)/(1+x(x+1)))=tan^(−1) (x+1)−tan^(−1) x A=Σ_(n=1) ^(15) tan^(−1) (x+1)−tan^(−1) x=tan^(−1) 2−tan^(−1) 1+tan^(−1) 3−tan^(−1) 2+.. A=tan^(−1) 16−tan^(−1) 1=tan^(−1) ((15)/(17)) tanA=((15)/(17))

$${f}\left({x}\right)={tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}={tan}^{−\mathrm{1}} \frac{{x}+\mathrm{1}−{x}}{\mathrm{1}+{x}\left({x}+\mathrm{1}\right)}={tan}^{−\mathrm{1}} \left({x}+\mathrm{1}\right)−{tan}^{−\mathrm{1}} {x} \\ $$$${A}=\underset{{n}=\mathrm{1}} {\overset{\mathrm{15}} {\sum}}{tan}^{−\mathrm{1}} \left({x}+\mathrm{1}\right)−{tan}^{−\mathrm{1}} {x}={tan}^{−\mathrm{1}} \mathrm{2}−{tan}^{−\mathrm{1}} \mathrm{1}+{tan}^{−\mathrm{1}} \mathrm{3}−{tan}^{−\mathrm{1}} \mathrm{2}+.. \\ $$$${A}={tan}^{−\mathrm{1}} \mathrm{16}−{tan}^{−\mathrm{1}} \mathrm{1}={tan}^{−\mathrm{1}} \frac{\mathrm{15}}{\mathrm{17}} \\ $$$${tanA}=\frac{\mathrm{15}}{\mathrm{17}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply