Question Number 105743 by Skabetix last updated on 31/Jul/20

Commented by Skabetix last updated on 31/Jul/20
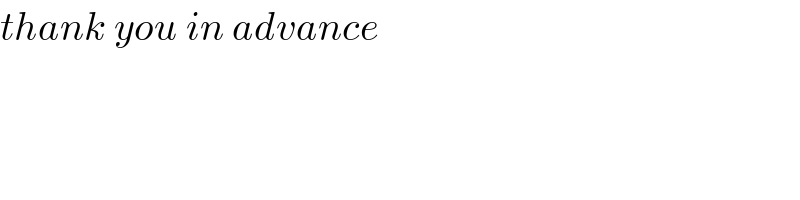
$${thank}\:{you}\:{in}\:{advance} \\ $$
Answered by john santu last updated on 31/Jul/20
![∫_a ^b (((df(x))/dx)/( (√(1+f^( 2) (x))))) dx + f^( 3) (b)−f^( 3) (a) ∫_a ^b ((df(x))/( (√(1+f^2 (x))))) + f^3 (b)−f^3 (a) [ ln ∣f(x)+(√(1+f^2 (x))) ∣ ]_a ^b +f^3 (b)−f^3 (a) ln∣ ((f(b)+(√(1+f^2 (b))))/(f(a)+(√(1+f^( 2) (a)))))∣ + f^3 (b)−f^( 3) (a)](https://www.tinkutara.com/question/Q105772.png)
$$\underset{{a}} {\overset{{b}} {\int}}\:\frac{\frac{{df}\left({x}\right)}{{dx}}}{\:\sqrt{\mathrm{1}+{f}^{\:\mathrm{2}} \left({x}\right)}}\:{dx}\:+\:{f}^{\:\mathrm{3}} \left({b}\right)−{f}^{\:\mathrm{3}} \left({a}\right) \\ $$$$\underset{{a}} {\overset{{b}} {\int}}\:\frac{{df}\left({x}\right)}{\:\sqrt{\mathrm{1}+{f}\:^{\mathrm{2}} \left({x}\right)}}\:+\:{f}\:^{\mathrm{3}} \left({b}\right)−{f}\:^{\mathrm{3}} \left({a}\right)\: \\ $$$$\:\:\left[\:\mathrm{ln}\:\mid{f}\left({x}\right)+\sqrt{\mathrm{1}+{f}\:^{\mathrm{2}} \left({x}\right)}\:\mid\:\right]_{{a}} ^{{b}} \:+{f}\:^{\mathrm{3}} \left({b}\right)−{f}\:^{\mathrm{3}} \left({a}\right) \\ $$$$\mathrm{ln}\mid\:\frac{{f}\left({b}\right)+\sqrt{\mathrm{1}+{f}\:^{\mathrm{2}} \left({b}\right)}}{{f}\left({a}\right)+\sqrt{\mathrm{1}+{f}^{\:\mathrm{2}} \left({a}\right)}}\mid\:+\:{f}\:^{\mathrm{3}} \left({b}\right)−{f}^{\:\mathrm{3}} \left({a}\right) \\ $$
