Menu Close

Question-105769

Tinku Tara 0 Comments
Pin




Question Number 105769 by ajfour last updated on 31/Jul/20
Commented by ajfour last updated on 31/Jul/20
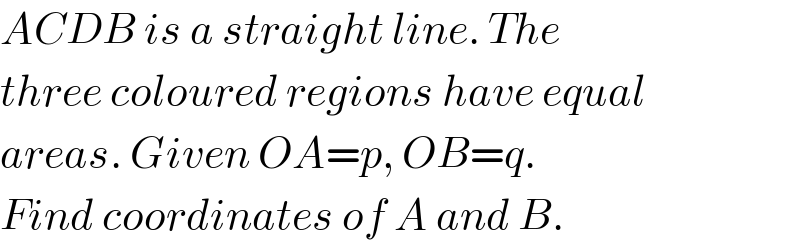
ACDB is a straight line. The three coloured regions have equal areas. Given OA=p, OB=q. Find coordinates of A and B.
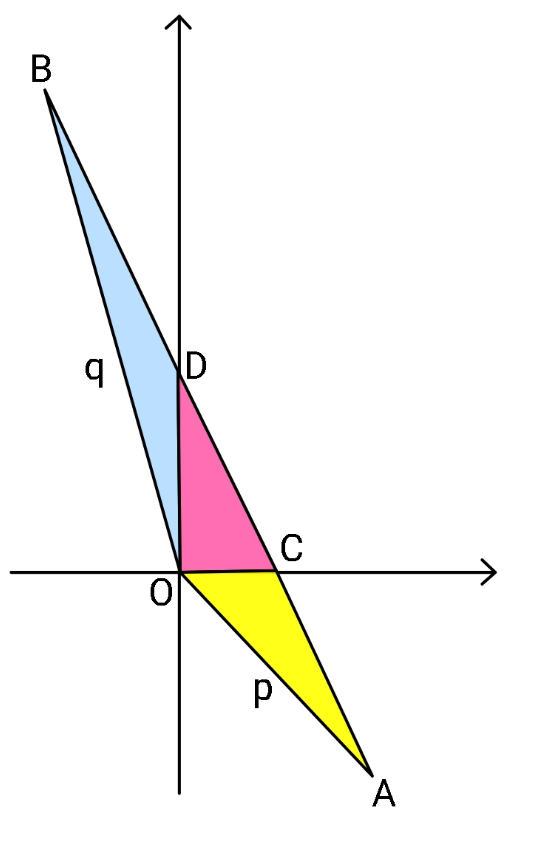
$${ACDB}\:{is}\:{a}\:{straight}\:{line}.\:{The} \\ $$$${three}\:{coloured}\:{regions}\:{have}\:{equal} \\ $$$${areas}.\:{Given}\:{OA}={p},\:{OB}={q}. \\ $$$${Find}\:{coordinates}\:{of}\:{A}\:{and}\:{B}. \\ $$
Answered by mr W last updated on 31/Jul/20
A((√(p^2 −h^2 )),h) B(k,(√(q^2 −k^2 ))) eqn. of AB: ((y−h)/( (√(q^2 −k^2 ))−h))=((x−(√(p^2 −h^2 )))/(k−(√(p^2 −h^2 )))) x_C =(√(p^2 −h^2 ))−((h(k−(√(p^2 −h^2 ))))/( (√(q^2 −k^2 ))−h)) y_D =h−((((√(q^2 −k^2 ))−h)(√(p^2 −h^2 )))/(k−(√(p^2 −h^2 )))) A_(red) =A_(yellow) ⇒−h=y_D =h−((((√(q^2 −k^2 ))−h)(√(p^2 −h^2 )))/(k−(√(p^2 −h^2 )))) ⇒((((√(q^2 −k^2 ))−h)(√(p^2 −h^2 )))/(k−(√(p^2 −h^2 ))))=2h ...(i) A_(blue) =A_(red) ⇒−k=x_C =(√(p^2 −h^2 ))−((h(k−(√(p^2 −h^2 ))))/( (√(q^2 −k^2 ))−h)) ⇒((h(k−(√(p^2 −h^2 ))))/( (√(q^2 −k^2 ))−h))=k+(√(p^2 −h^2 )) ...(ii) (i)×(ii): (√(p^2 −h^2 ))=2(k+(√(p^2 −h^2 ))) ⇒k=−((√(p^2 −h^2 ))/2) from (i): ((k−(√(p^2 −h^2 )))/( (√(q^2 −k^2 ))−h))=((√(p^2 −h^2 ))/(2h)) 4q^2 −p^2 =15h^2 ⇒h=−(√((4q^2 −p^2 )/(15))) ⇒k=−(√((4p^2 −q^2 )/(15)))
$${A}\left(\sqrt{{p}^{\mathrm{2}} −{h}^{\mathrm{2}} },{h}\right) \\ $$$${B}\left({k},\sqrt{{q}^{\mathrm{2}} −{k}^{\mathrm{2}} }\right) \\ $$$${eqn}.\:{of}\:{AB}: \\ $$$$\frac{{y}−{h}}{\:\sqrt{{q}^{\mathrm{2}} −{k}^{\mathrm{2}} }−{h}}=\frac{{x}−\sqrt{{p}^{\mathrm{2}} −{h}^{\mathrm{2}} }}{{k}−\sqrt{{p}^{\mathrm{2}} −{h}^{\mathrm{2}} }} \\ $$$${x}_{{C}} =\sqrt{{p}^{\mathrm{2}} −{h}^{\mathrm{2}} }−\frac{{h}\left({k}−\sqrt{{p}^{\mathrm{2}} −{h}^{\mathrm{2}} }\right)}{\:\sqrt{{q}^{\mathrm{2}} −{k}^{\mathrm{2}} }−{h}} \\ $$$${y}_{{D}} ={h}−\frac{\left(\sqrt{{q}^{\mathrm{2}} −{k}^{\mathrm{2}} }−{h}\right)\sqrt{{p}^{\mathrm{2}} −{h}^{\mathrm{2}} }}{{k}−\sqrt{{p}^{\mathrm{2}} −{h}^{\mathrm{2}} }} \\ $$$${A}_{{red}} ={A}_{{yellow}} \\ $$$$\Rightarrow−{h}={y}_{{D}} ={h}−\frac{\left(\sqrt{{q}^{\mathrm{2}} −{k}^{\mathrm{2}} }−{h}\right)\sqrt{{p}^{\mathrm{2}} −{h}^{\mathrm{2}} }}{{k}−\sqrt{{p}^{\mathrm{2}} −{h}^{\mathrm{2}} }} \\ $$$$\Rightarrow\frac{\left(\sqrt{{q}^{\mathrm{2}} −{k}^{\mathrm{2}} }−{h}\right)\sqrt{{p}^{\mathrm{2}} −{h}^{\mathrm{2}} }}{{k}−\sqrt{{p}^{\mathrm{2}} −{h}^{\mathrm{2}} }}=\mathrm{2}{h}\:\:\:…\left({i}\right) \\ $$$${A}_{{blue}} ={A}_{{red}} \\ $$$$\Rightarrow−{k}={x}_{{C}} =\sqrt{{p}^{\mathrm{2}} −{h}^{\mathrm{2}} }−\frac{{h}\left({k}−\sqrt{{p}^{\mathrm{2}} −{h}^{\mathrm{2}} }\right)}{\:\sqrt{{q}^{\mathrm{2}} −{k}^{\mathrm{2}} }−{h}} \\ $$$$\Rightarrow\frac{{h}\left({k}−\sqrt{{p}^{\mathrm{2}} −{h}^{\mathrm{2}} }\right)}{\:\sqrt{{q}^{\mathrm{2}} −{k}^{\mathrm{2}} }−{h}}={k}+\sqrt{{p}^{\mathrm{2}} −{h}^{\mathrm{2}} }\:\:\:…\left({ii}\right) \\ $$$$\left({i}\right)×\left({ii}\right): \\ $$$$\sqrt{{p}^{\mathrm{2}} −{h}^{\mathrm{2}} }=\mathrm{2}\left({k}+\sqrt{{p}^{\mathrm{2}} −{h}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow{k}=−\frac{\sqrt{{p}^{\mathrm{2}} −{h}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$${from}\:\left({i}\right): \\ $$$$\frac{{k}−\sqrt{{p}^{\mathrm{2}} −{h}^{\mathrm{2}} }}{\:\sqrt{{q}^{\mathrm{2}} −{k}^{\mathrm{2}} }−{h}}=\frac{\sqrt{{p}^{\mathrm{2}} −{h}^{\mathrm{2}} }}{\mathrm{2}{h}} \\ $$$$\mathrm{4}{q}^{\mathrm{2}} −{p}^{\mathrm{2}} =\mathrm{15}{h}^{\mathrm{2}} \\ $$$$\Rightarrow{h}=−\sqrt{\frac{\mathrm{4}{q}^{\mathrm{2}} −{p}^{\mathrm{2}} }{\mathrm{15}}} \\ $$$$\Rightarrow{k}=−\sqrt{\frac{\mathrm{4}{p}^{\mathrm{2}} −{q}^{\mathrm{2}} }{\mathrm{15}}} \\ $$
Commented by mr W last updated on 31/Jul/20
Commented by ajfour last updated on 01/Aug/20
Thanks Sir, you spirit my level up!
$${Thanks}\:{Sir},\:{you}\:{spirit}\:{my}\:{level} \\ $$$${up}! \\ $$
Answered by ajfour last updated on 01/Aug/20
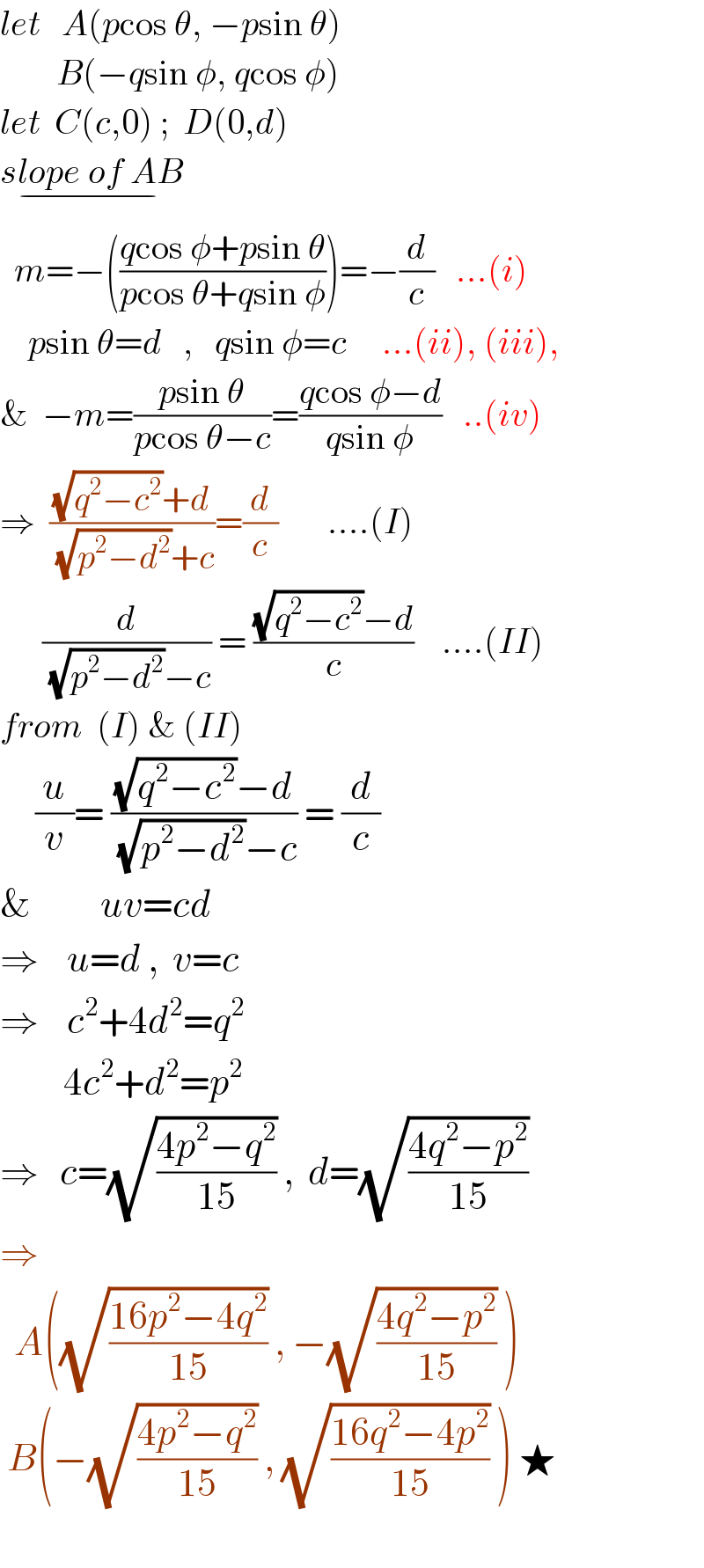
let A(pcos θ, −psin θ) B(−qsin φ, qcos φ) let C(c,0) ; D(0,d) slope of AB_(−) m=−(((qcos φ+psin θ)/(pcos θ+qsin φ)))=−(d/c) ...(i) psin θ=d , qsin φ=c ...(ii), (iii), & −m=((psin θ)/(pcos θ−c))=((qcos φ−d)/(qsin φ)) ..(iv) ⇒ (((√(q^2 −c^2 ))+d)/( (√(p^2 −d^2 ))+c))=(d/c) ....(I) (d/( (√(p^2 −d^2 ))−c)) = (((√(q^2 −c^2 ))−d)/c) ....(II) from (I) & (II) (u/v)= (((√(q^2 −c^2 ))−d)/( (√(p^2 −d^2 ))−c)) = (d/c) & uv=cd ⇒ u=d , v=c ⇒ c^2 +4d^2 =q^2 4c^2 +d^2 =p^2 ⇒ c=(√((4p^2 −q^2 )/(15))) , d=(√((4q^2 −p^2 )/(15))) ⇒ A((√((16p^2 −4q^2 )/(15))) , −(√((4q^2 −p^2 )/(15))) ) B(−(√((4p^2 −q^2 )/(15))) , (√((16q^2 −4p^2 )/(15))) ) ★
$${let}\:\:\:{A}\left({p}\mathrm{cos}\:\theta,\:−{p}\mathrm{sin}\:\theta\right) \\ $$$$\:\:\:\:\:\:\:\:{B}\left(−{q}\mathrm{sin}\:\phi,\:{q}\mathrm{cos}\:\phi\right) \\ $$$${let}\:\:{C}\left({c},\mathrm{0}\right)\:;\:\:{D}\left(\mathrm{0},{d}\right) \\ $$$$\underset{−} {{slope}\:{of}\:{AB}} \\ $$$$\:\:{m}=−\left(\frac{{q}\mathrm{cos}\:\phi+{p}\mathrm{sin}\:\theta}{{p}\mathrm{cos}\:\theta+{q}\mathrm{sin}\:\phi}\right)=−\frac{{d}}{{c}}\:\:\:…\left({i}\right) \\ $$$$\:\:\:\:{p}\mathrm{sin}\:\theta={d}\:\:\:,\:\:\:{q}\mathrm{sin}\:\phi={c}\:\:\:\:\:…\left({ii}\right),\:\left({iii}\right), \\ $$$$\&\:\:−{m}=\frac{{p}\mathrm{sin}\:\theta}{{p}\mathrm{cos}\:\theta−{c}}=\frac{{q}\mathrm{cos}\:\phi−{d}}{{q}\mathrm{sin}\:\phi}\:\:\:..\left({iv}\right) \\ $$$$\Rightarrow\:\:\frac{\sqrt{{q}^{\mathrm{2}} −{c}^{\mathrm{2}} }+{d}}{\:\sqrt{{p}^{\mathrm{2}} −{d}^{\mathrm{2}} }+{c}}=\frac{{d}}{{c}}\:\:\:\:\:\:\:….\left({I}\right) \\ $$$$\:\:\:\:\:\:\frac{{d}}{\:\sqrt{{p}^{\mathrm{2}} −{d}^{\mathrm{2}} }−{c}}\:=\:\frac{\sqrt{{q}^{\mathrm{2}} −{c}^{\mathrm{2}} }−{d}}{{c}}\:\:\:\:….\left({II}\right) \\ $$$${from}\:\:\left({I}\right)\:\&\:\left({II}\right) \\ $$$$\:\:\:\:\:\frac{{u}}{{v}}=\:\frac{\sqrt{{q}^{\mathrm{2}} −{c}^{\mathrm{2}} }−{d}}{\:\sqrt{{p}^{\mathrm{2}} −{d}^{\mathrm{2}} }−{c}}\:=\:\frac{{d}}{{c}} \\ $$$$\&\:\:\:\:\:\:\:\:\:\:{uv}={cd} \\ $$$$\Rightarrow\:\:\:\:{u}={d}\:,\:\:{v}={c} \\ $$$$\Rightarrow\:\:\:\:{c}^{\mathrm{2}} +\mathrm{4}{d}^{\mathrm{2}} ={q}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{4}{c}^{\mathrm{2}} +{d}^{\mathrm{2}} ={p}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:{c}=\sqrt{\frac{\mathrm{4}{p}^{\mathrm{2}} −{q}^{\mathrm{2}} }{\mathrm{15}}}\:,\:\:{d}=\sqrt{\frac{\mathrm{4}{q}^{\mathrm{2}} −{p}^{\mathrm{2}} }{\mathrm{15}}} \\ $$$$\Rightarrow \\ $$$$\:\:{A}\left(\sqrt{\frac{\mathrm{16}{p}^{\mathrm{2}} −\mathrm{4}{q}^{\mathrm{2}} }{\mathrm{15}}}\:,\:−\sqrt{\frac{\mathrm{4}{q}^{\mathrm{2}} −{p}^{\mathrm{2}} }{\mathrm{15}}}\:\right) \\ $$$$\:{B}\left(−\sqrt{\frac{\mathrm{4}{p}^{\mathrm{2}} −{q}^{\mathrm{2}} }{\mathrm{15}}}\:,\:\sqrt{\frac{\mathrm{16}{q}^{\mathrm{2}} −\mathrm{4}{p}^{\mathrm{2}} }{\mathrm{15}}}\:\right)\:\bigstar \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *