Question Number 105799 by mohammad17 last updated on 31/Jul/20
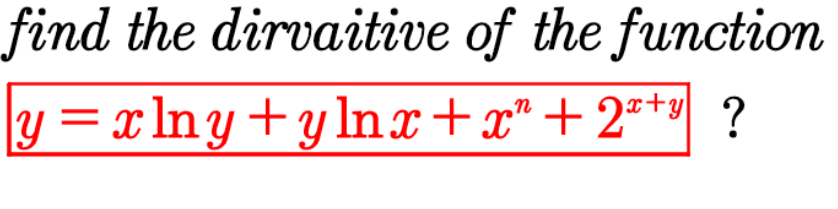
Answered by Dwaipayan Shikari last updated on 31/Jul/20
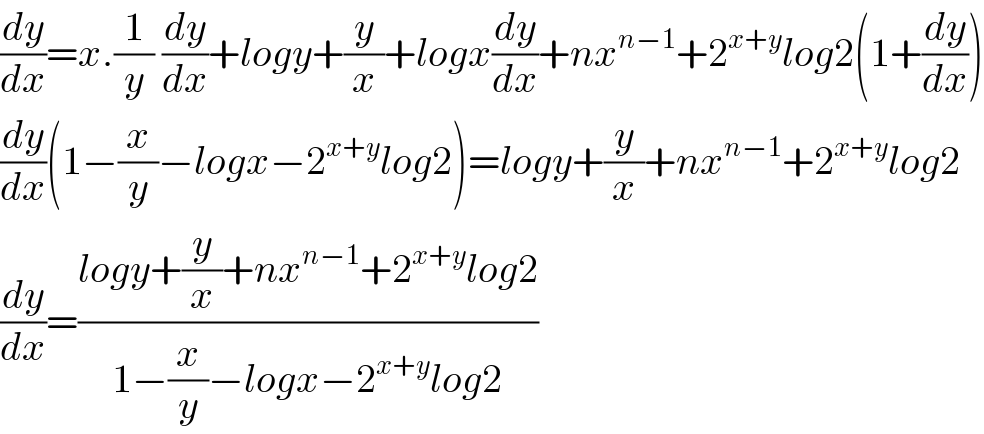
$$\frac{{dy}}{{dx}}={x}.\frac{\mathrm{1}}{{y}}\:\frac{{dy}}{{dx}}+{logy}+\frac{{y}}{{x}}+{logx}\frac{{dy}}{{dx}}+{nx}^{{n}−\mathrm{1}} +\mathrm{2}^{{x}+{y}} {log}\mathrm{2}\left(\mathrm{1}+\frac{{dy}}{{dx}}\right) \\ $$$$\frac{{dy}}{{dx}}\left(\mathrm{1}−\frac{{x}}{{y}}−{logx}−\mathrm{2}^{{x}+{y}} {log}\mathrm{2}\right)={logy}+\frac{{y}}{{x}}+{nx}^{{n}−\mathrm{1}} +\mathrm{2}^{{x}+{y}} {log}\mathrm{2} \\ $$$$\frac{{dy}}{{dx}}=\frac{{logy}+\frac{{y}}{{x}}+{nx}^{{n}−\mathrm{1}} +\mathrm{2}^{{x}+{y}} {log}\mathrm{2}}{\mathrm{1}−\frac{{x}}{{y}}−{logx}−\mathrm{2}^{{x}+{y}} {log}\mathrm{2}} \\ $$
Commented by mohammad17 last updated on 31/Jul/20

$${thank}\:{you}\:{sir} \\ $$
