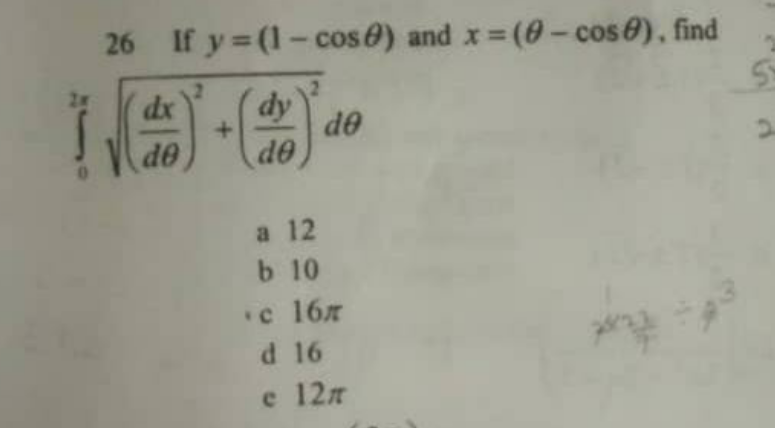Question Number 105815 by I want to learn more last updated on 31/Jul/20
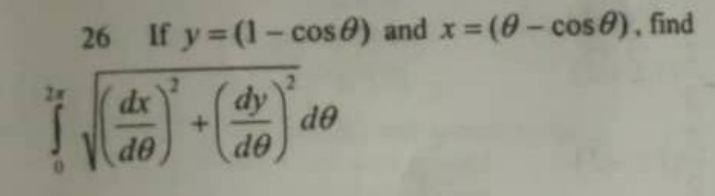
Answered by john santu last updated on 01/Aug/20
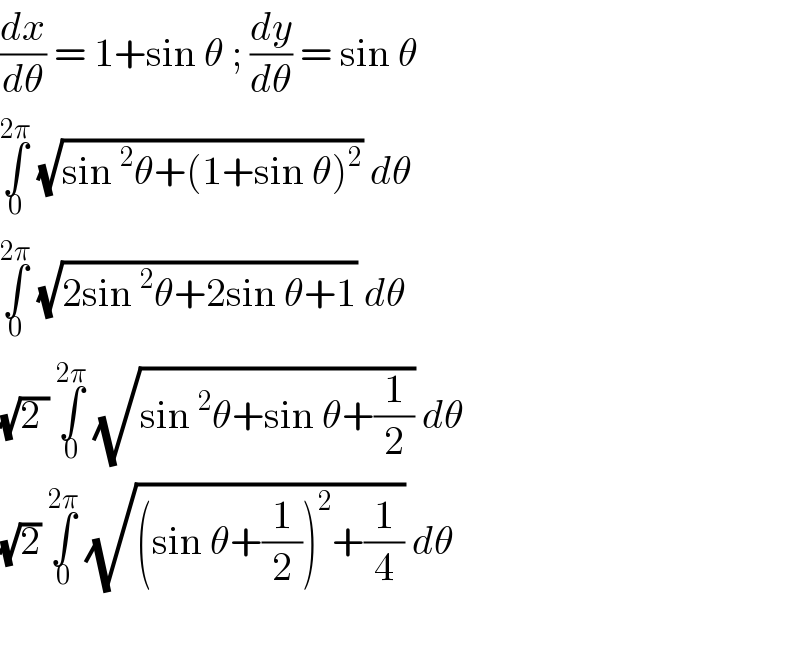
$$\frac{{dx}}{{d}\theta}\:=\:\mathrm{1}+\mathrm{sin}\:\theta\:;\:\frac{{dy}}{{d}\theta}\:=\:\mathrm{sin}\:\theta \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\:\sqrt{\mathrm{sin}\:^{\mathrm{2}} \theta+\left(\mathrm{1}+\mathrm{sin}\:\theta\right)^{\mathrm{2}} }\:{d}\theta\: \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\:\sqrt{\mathrm{2sin}\:^{\mathrm{2}} \theta+\mathrm{2sin}\:\theta+\mathrm{1}}\:{d}\theta \\ $$$$\sqrt{\mathrm{2}\:}\:\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\:\sqrt{\mathrm{sin}\:^{\mathrm{2}} \theta+\mathrm{sin}\:\theta+\frac{\mathrm{1}}{\mathrm{2}}}\:{d}\theta \\ $$$$\sqrt{\mathrm{2}}\:\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\:\sqrt{\left(\mathrm{sin}\:\theta+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}}\:{d}\theta\: \\ $$$$ \\ $$
Commented by bemath last updated on 01/Aug/20
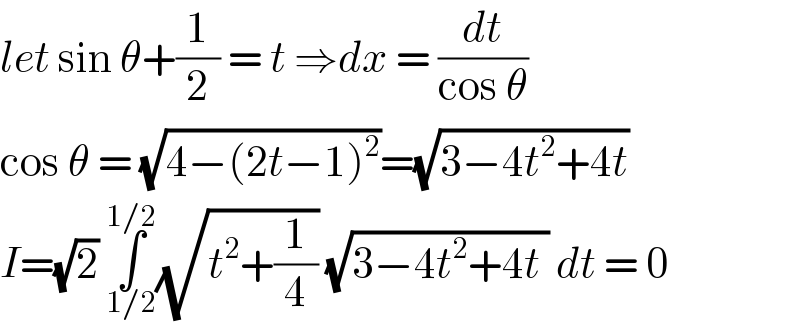
$${let}\:\mathrm{sin}\:\theta+\frac{\mathrm{1}}{\mathrm{2}}\:=\:{t}\:\Rightarrow{dx}\:=\:\frac{{dt}}{\mathrm{cos}\:\theta} \\ $$$$\mathrm{cos}\:\theta\:=\:\sqrt{\mathrm{4}−\left(\mathrm{2}{t}−\mathrm{1}\right)^{\mathrm{2}} }=\sqrt{\mathrm{3}−\mathrm{4}{t}^{\mathrm{2}} +\mathrm{4}{t}} \\ $$$${I}=\sqrt{\mathrm{2}}\:\underset{\mathrm{1}/\mathrm{2}} {\overset{\mathrm{1}/\mathrm{2}} {\int}}\sqrt{{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}}\:\sqrt{\mathrm{3}−\mathrm{4}{t}^{\mathrm{2}} +\mathrm{4}{t}\:}\:{dt}\:=\:\mathrm{0} \\ $$
Commented by I want to learn more last updated on 01/Aug/20