Menu Close

Question-105877

Tinku Tara 0 Comments
Pin




Question Number 105877 by john santu last updated on 01/Aug/20
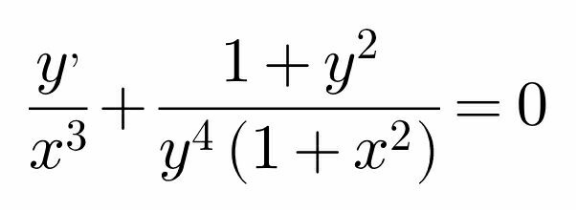
Answered by bemath last updated on 01/Aug/20
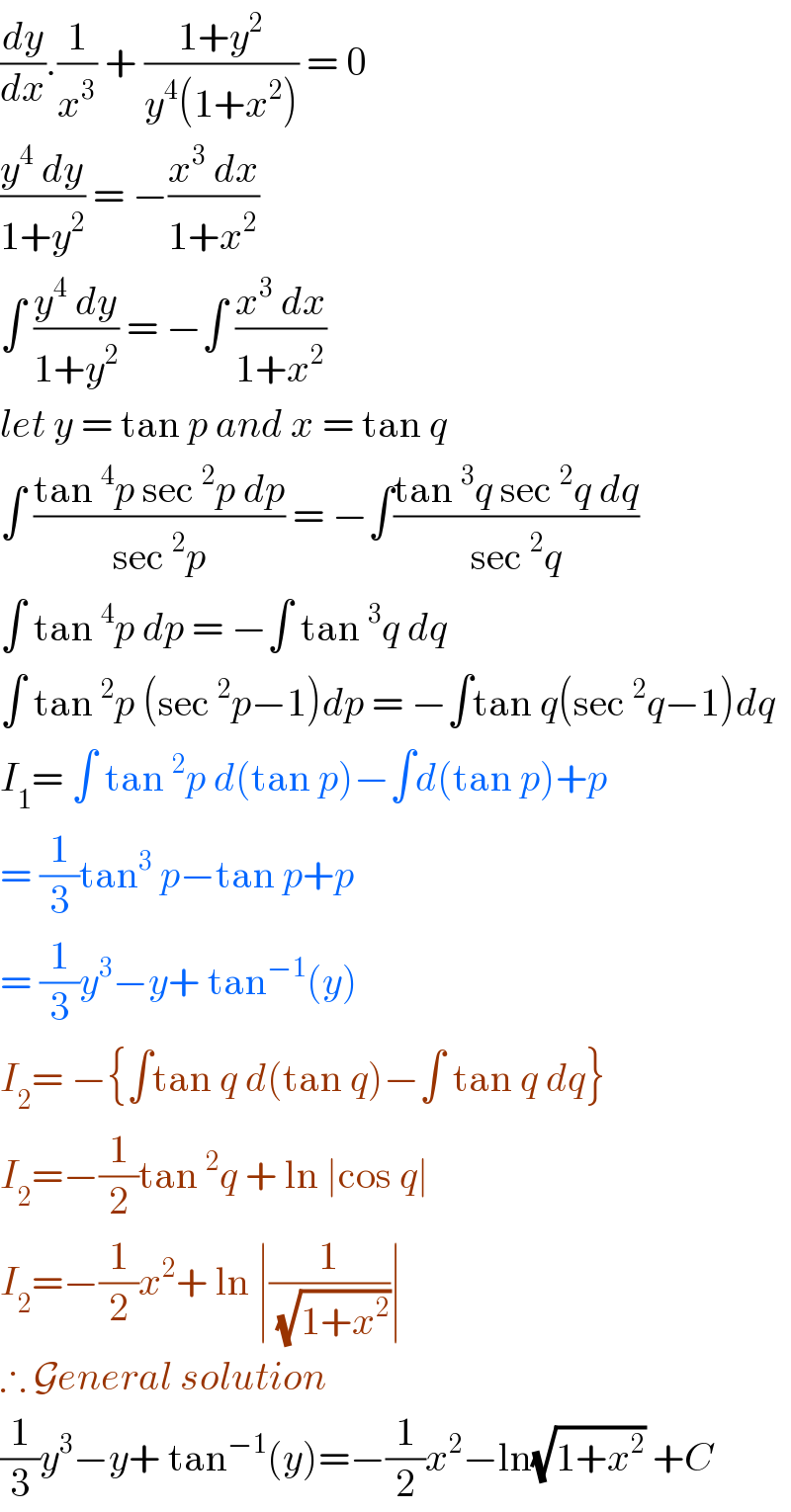
(dy/dx).(1/x^3 ) + ((1+y^2 )/(y^4 (1+x^2 ))) = 0 ((y^4 dy)/(1+y^2 )) = −((x^3 dx)/(1+x^2 )) ∫ ((y^4 dy)/(1+y^2 )) = −∫ ((x^3 dx)/(1+x^2 )) let y = tan p and x = tan q ∫ ((tan^4 p sec^2 p dp)/(sec^2 p)) = −∫((tan^3 q sec^2 q dq)/(sec^2 q)) ∫ tan^4 p dp = −∫ tan^3 q dq ∫ tan^2 p (sec^2 p−1)dp = −∫tan q(sec^2 q−1)dq I_1 = ∫ tan^2 p d(tan p)−∫d(tan p)+p = (1/3)tan^3 p−tan p+p = (1/3)y^3 −y+ tan^(−1) (y) I_2 = −{∫tan q d(tan q)−∫ tan q dq} I_2 =−(1/2)tan^2 q + ln ∣cos q∣ I_2 =−(1/2)x^2 + ln ∣(1/( (√(1+x^2 ))))∣ ∴ General solution (1/3)y^3 −y+ tan^(−1) (y)=−(1/2)x^2 −ln(√(1+x^2 )) +C
$$\frac{{dy}}{{dx}}.\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\:+\:\frac{\mathrm{1}+{y}^{\mathrm{2}} }{{y}^{\mathrm{4}} \left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:=\:\mathrm{0} \\ $$$$\frac{{y}^{\mathrm{4}} \:{dy}}{\mathrm{1}+{y}^{\mathrm{2}} }\:=\:−\frac{{x}^{\mathrm{3}} \:{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\: \\ $$$$\int\:\frac{{y}^{\mathrm{4}} \:{dy}}{\mathrm{1}+{y}^{\mathrm{2}} }\:=\:−\int\:\frac{{x}^{\mathrm{3}} \:{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$${let}\:{y}\:=\:\mathrm{tan}\:{p}\:{and}\:{x}\:=\:\mathrm{tan}\:{q}\: \\ $$$$\int\:\frac{\mathrm{tan}\:^{\mathrm{4}} {p}\:\mathrm{sec}\:^{\mathrm{2}} {p}\:{dp}}{\mathrm{sec}\:^{\mathrm{2}} {p}}\:=\:−\int\frac{\mathrm{tan}\:^{\mathrm{3}} {q}\:\mathrm{sec}\:^{\mathrm{2}} {q}\:{dq}}{\mathrm{sec}\:^{\mathrm{2}} {q}} \\ $$$$\int\:\mathrm{tan}\:^{\mathrm{4}} {p}\:{dp}\:=\:−\int\:\mathrm{tan}\:^{\mathrm{3}} {q}\:{dq}\: \\ $$$$\int\:\mathrm{tan}\:^{\mathrm{2}} {p}\:\left(\mathrm{sec}\:^{\mathrm{2}} {p}−\mathrm{1}\right){dp}\:=\:−\int\mathrm{tan}\:{q}\left(\mathrm{sec}\:^{\mathrm{2}} {q}−\mathrm{1}\right){dq} \\ $$$${I}_{\mathrm{1}} =\:\int\:\mathrm{tan}\:^{\mathrm{2}} {p}\:{d}\left(\mathrm{tan}\:{p}\right)−\int{d}\left(\mathrm{tan}\:{p}\right)+{p} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{\mathrm{3}} \:{p}−\mathrm{tan}\:{p}+{p} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{3}}{y}^{\mathrm{3}} −{y}+\:\mathrm{tan}^{−\mathrm{1}} \left({y}\right) \\ $$$${I}_{\mathrm{2}} =\:−\left\{\int\mathrm{tan}\:{q}\:{d}\left(\mathrm{tan}\:{q}\right)−\int\:\mathrm{tan}\:{q}\:{dq}\right\} \\ $$$${I}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}\:^{\mathrm{2}} {q}\:+\:\mathrm{ln}\:\mid\mathrm{cos}\:{q}\mid\: \\ $$$${I}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +\:\mathrm{ln}\:\mid\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\mid\: \\ $$$$\therefore\:\mathcal{G}{eneral}\:{solution} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}{y}^{\mathrm{3}} −{y}+\:\mathrm{tan}^{−\mathrm{1}} \left({y}\right)=−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} −\mathrm{ln}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:+{C}\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *