Question-105883

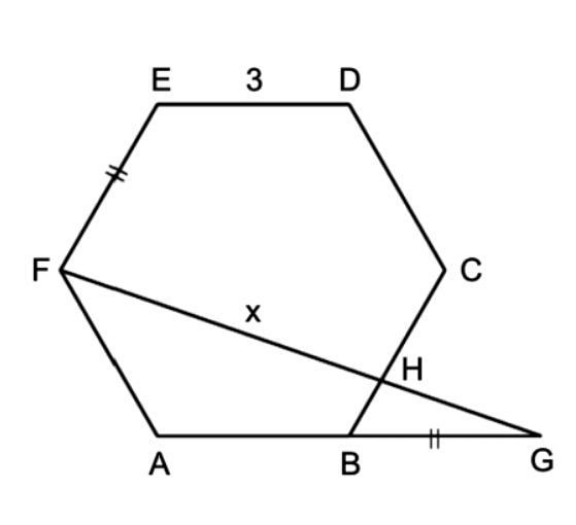
Question Number 105883 by bemath last updated on 01/Aug/20

Answered by mr W last updated on 01/Aug/20

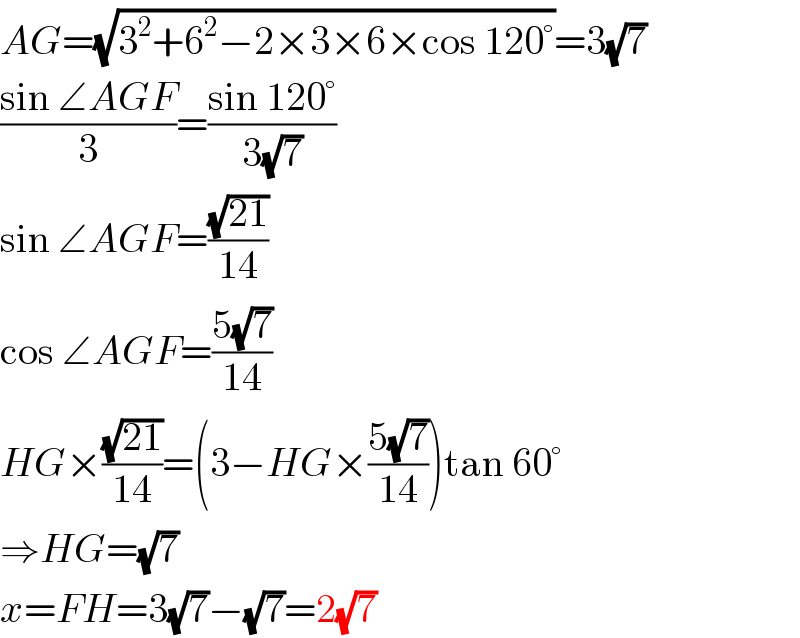
AG=(√(3^2 +6^2 −2×3×6×cos 120°))=3(√7) ((sin ∠AGF)/3)=((sin 120°)/(3(√7))) sin ∠AGF=((√(21))/(14)) cos ∠AGF=((5(√7))/(14)) HG×((√(21))/(14))=(3−HG×((5(√7))/(14)))tan 60° ⇒HG=(√7) x=FH=3(√7)−(√7)=2(√7)

$${AG}=\sqrt{\mathrm{3}^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} −\mathrm{2}×\mathrm{3}×\mathrm{6}×\mathrm{cos}\:\mathrm{120}°}=\mathrm{3}\sqrt{\mathrm{7}} \\ $$$$\frac{\mathrm{sin}\:\angle{AGF}}{\mathrm{3}}=\frac{\mathrm{sin}\:\mathrm{120}°}{\mathrm{3}\sqrt{\mathrm{7}}} \\ $$$$\mathrm{sin}\:\angle{AGF}=\frac{\sqrt{\mathrm{21}}}{\mathrm{14}} \\ $$$$\mathrm{cos}\:\angle{AGF}=\frac{\mathrm{5}\sqrt{\mathrm{7}}}{\mathrm{14}} \\ $$$${HG}×\frac{\sqrt{\mathrm{21}}}{\mathrm{14}}=\left(\mathrm{3}−{HG}×\frac{\mathrm{5}\sqrt{\mathrm{7}}}{\mathrm{14}}\right)\mathrm{tan}\:\mathrm{60}° \\ $$$$\Rightarrow{HG}=\sqrt{\mathrm{7}} \\ $$$${x}={FH}=\mathrm{3}\sqrt{\mathrm{7}}−\sqrt{\mathrm{7}}=\mathrm{2}\sqrt{\mathrm{7}} \\ $$

Commented by bemath last updated on 01/Aug/20

$${thank}\:{you}\:{sir} \\ $$

Answered by mr W last updated on 01/Aug/20

Commented by mr W last updated on 01/Aug/20

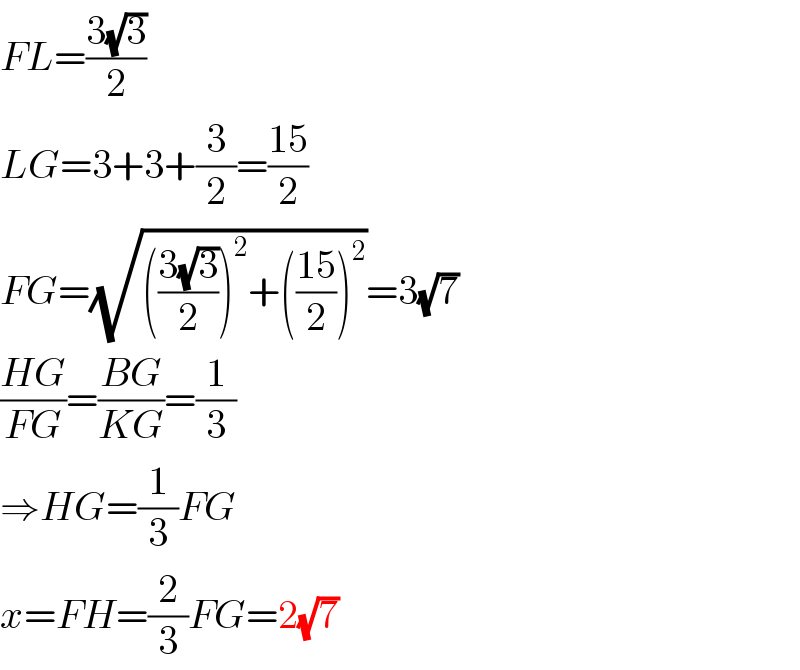
FL=((3(√3))/2) LG=3+3+(3/2)=((15)/2) FG=(√((((3(√3))/2))^2 +(((15)/2))^2 ))=3(√7) ((HG)/(FG))=((BG)/(KG))=(1/3) ⇒HG=(1/3)FG x=FH=(2/3)FG=2(√7)

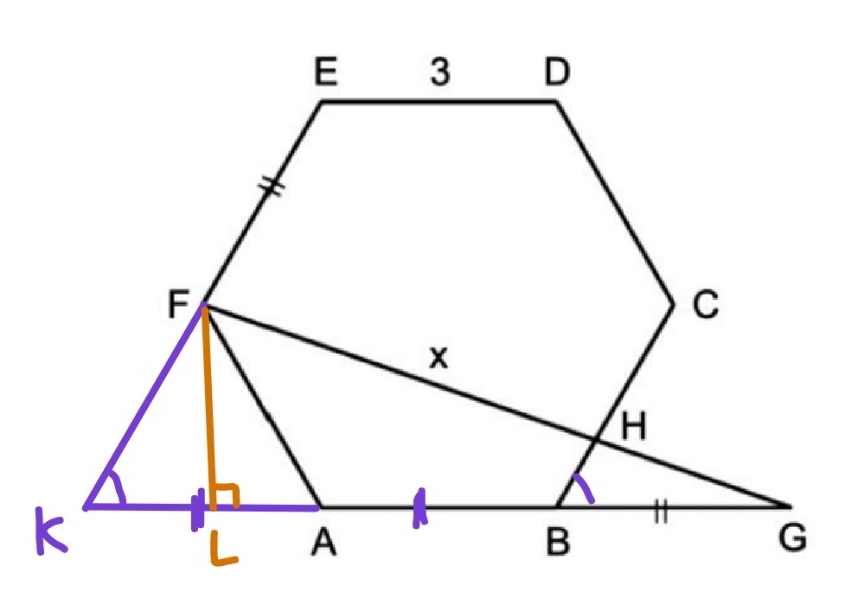
$${FL}=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${LG}=\mathrm{3}+\mathrm{3}+\frac{\mathrm{3}}{\mathrm{2}}=\frac{\mathrm{15}}{\mathrm{2}} \\ $$$${FG}=\sqrt{\left(\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{15}}{\mathrm{2}}\right)^{\mathrm{2}} }=\mathrm{3}\sqrt{\mathrm{7}} \\ $$$$\frac{{HG}}{{FG}}=\frac{{BG}}{{KG}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow{HG}=\frac{\mathrm{1}}{\mathrm{3}}{FG} \\ $$$${x}={FH}=\frac{\mathrm{2}}{\mathrm{3}}{FG}=\mathrm{2}\sqrt{\mathrm{7}} \\ $$

Answered by Coronavirus last updated on 01/Aug/20

en appliquant le theoreme d′ Alkashi au triangle AGF alors FG^2 =FA^2 +AG^2 +2FA^→ .AG^→ =(3)^2 +(6)^2 +2(3)(6)cos(FA^→ ;AG^→ ) car { ((AG=AB+BG)),((BG=FG=ED=3)) :} or (FA^→ ; AG^→ )= (π/3)⇒cos(FA^→ ; AG^→ )=(1/2) aussi FG^2 =9+36+18=63 donc FG=(√(63))

$$\mathrm{en}\:\mathrm{appliquant}\:\mathrm{le}\:\mathrm{theoreme}\:\mathrm{d}'\:\mathrm{Alkashi}\:\mathrm{au}\:\mathrm{triangle}\:\mathrm{A}{GF} \\ $$$${alors}\:{FG}^{\mathrm{2}} =\mathrm{FA}^{\mathrm{2}} +\mathrm{A}{G}^{\mathrm{2}} +\mathrm{2}{F}\overset{\rightarrow} {{A}}.{A}\overset{\rightarrow} {{G}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{3}\right)^{\mathrm{2}} +\left(\mathrm{6}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{3}\right)\left(\mathrm{6}\right)\mathrm{cos}\left({F}\overset{\rightarrow} {{A}};{A}\overset{\rightarrow} {{G}}\right)\:\:{car}\:\begin{cases}{{AG}={AB}+{BG}}\\{{BG}={FG}={ED}=\mathrm{3}}\end{cases} \\ $$$$\mathrm{or}\:\left(\mathrm{F}\overset{\rightarrow} {{A}}\:;\:{A}\overset{\rightarrow} {{G}}\right)=\:\frac{\pi}{\mathrm{3}}\Rightarrow\mathrm{cos}\left(\mathrm{F}\overset{\rightarrow} {{A}}\:;\:{A}\overset{\rightarrow} {{G}}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${aussi}\:\:{FG}^{\mathrm{2}} =\mathrm{9}+\mathrm{36}+\mathrm{18}=\mathrm{63} \\ $$$${donc}\:\:{FG}=\sqrt{\mathrm{63}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply