Menu Close

Question-105885

Tinku Tara 0 Comments
Pin




Question Number 105885 by mohammad17 last updated on 01/Aug/20
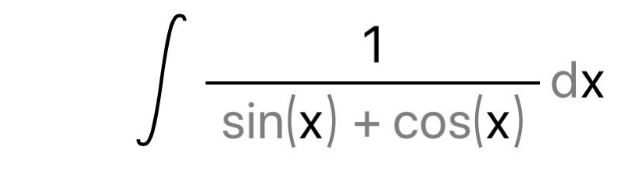
Answered by bemath last updated on 01/Aug/20
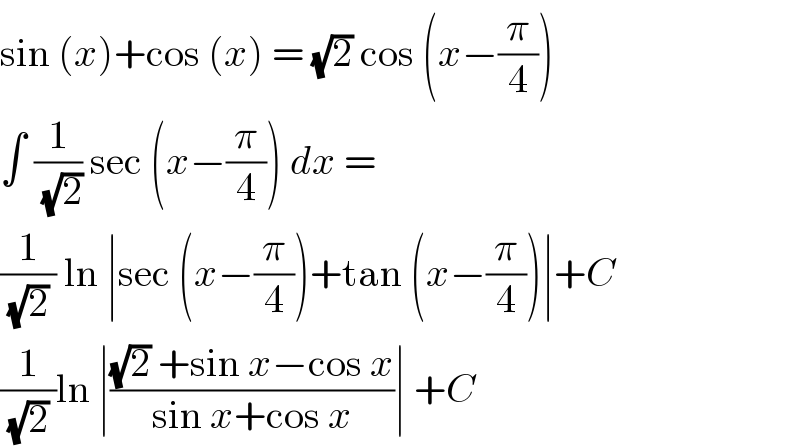
sin (x)+cos (x) = (√2) cos (x−(π/4)) ∫ (1/( (√2))) sec (x−(π/4)) dx = (1/( (√2) )) ln ∣sec (x−(π/4))+tan (x−(π/4))∣+C (1/( (√2) ))ln ∣(((√2) +sin x−cos x)/(sin x+cos x))∣ +C
$$\mathrm{sin}\:\left({x}\right)+\mathrm{cos}\:\left({x}\right)\:=\:\sqrt{\mathrm{2}}\:\mathrm{cos}\:\left({x}−\frac{\pi}{\mathrm{4}}\right) \\ $$$$\int\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\mathrm{sec}\:\left({x}−\frac{\pi}{\mathrm{4}}\right)\:{dx}\:=\: \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:}\:\mathrm{ln}\:\mid\mathrm{sec}\:\left({x}−\frac{\pi}{\mathrm{4}}\right)+\mathrm{tan}\:\left({x}−\frac{\pi}{\mathrm{4}}\right)\mid+{C} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:}\mathrm{ln}\:\mid\frac{\sqrt{\mathrm{2}}\:+\mathrm{sin}\:{x}−\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}\mid\:+{C} \\ $$
Commented by mohammad17 last updated on 01/Aug/20
very thank you sir
$${very}\:{thank}\:{you}\:{sir} \\ $$
Commented by bemath last updated on 01/Aug/20
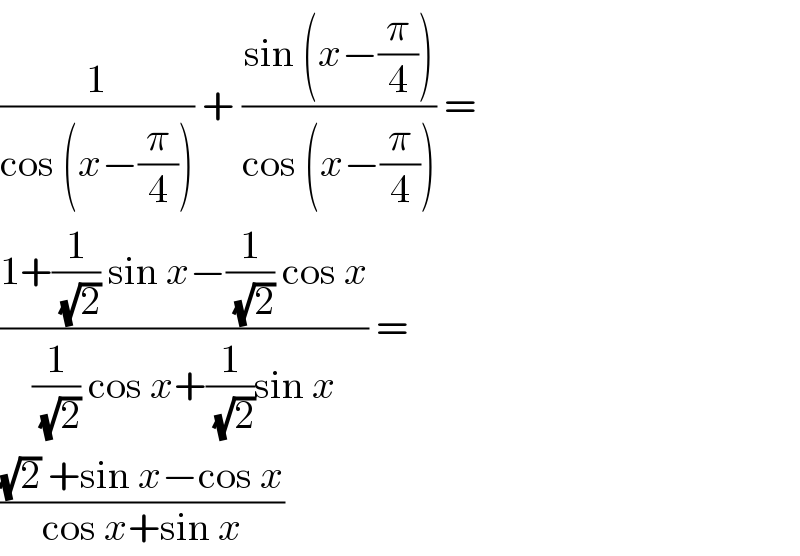
(1/(cos (x−(π/4)))) + ((sin (x−(π/4)))/(cos (x−(π/4)))) = ((1+(1/( (√2))) sin x−(1/( (√2))) cos x)/((1/( (√2))) cos x+(1/( (√2)))sin x)) = (((√2) +sin x−cos x)/(cos x+sin x))
$$\frac{\mathrm{1}}{\mathrm{cos}\:\left({x}−\frac{\pi}{\mathrm{4}}\right)}\:+\:\frac{\mathrm{sin}\:\left({x}−\frac{\pi}{\mathrm{4}}\right)}{\mathrm{cos}\:\left({x}−\frac{\pi}{\mathrm{4}}\right)}\:= \\ $$$$\frac{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\mathrm{sin}\:{x}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\mathrm{cos}\:{x}}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\mathrm{cos}\:{x}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{sin}\:{x}}\:= \\ $$$$\frac{\sqrt{\mathrm{2}}\:+\mathrm{sin}\:{x}−\mathrm{cos}\:{x}}{\mathrm{cos}\:{x}+\mathrm{sin}\:{x}} \\ $$
Answered by Dwaipayan Shikari last updated on 01/Aug/20
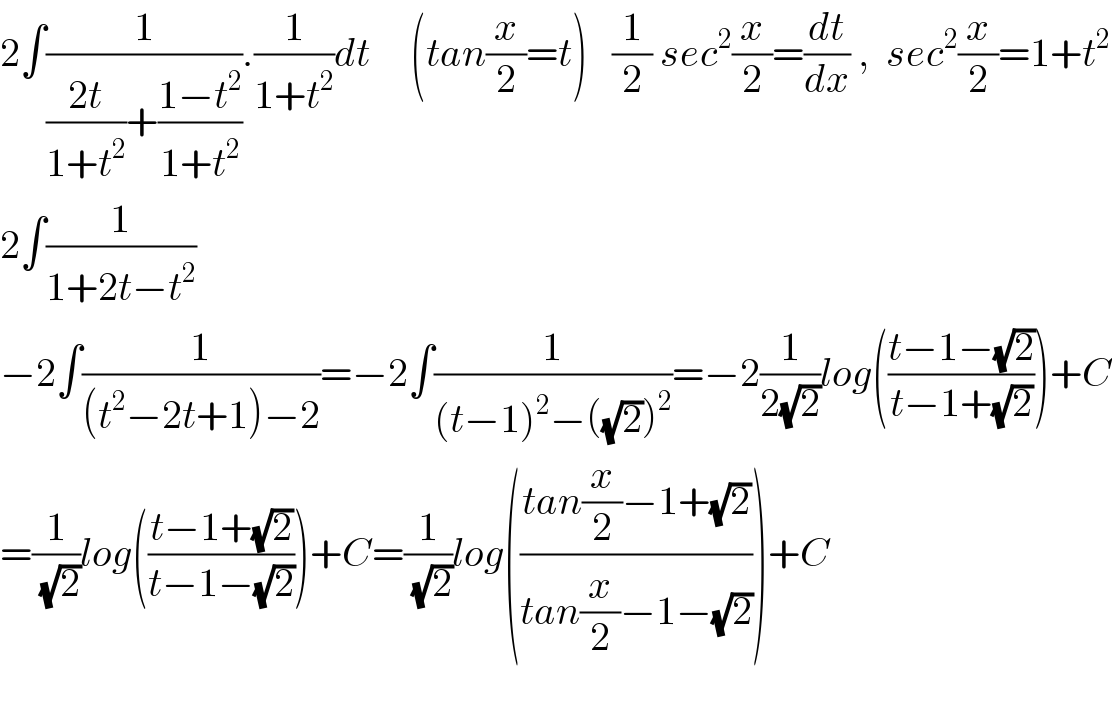
2∫(1/(((2t)/(1+t^2 ))+((1−t^2 )/(1+t^2 )))).(1/(1+t^2 ))dt (tan(x/2)=t) (1/2) sec^2 (x/2)=(dt/dx) , sec^2 (x/2)=1+t^2 2∫(1/(1+2t−t^2 )) −2∫(1/((t^2 −2t+1)−2))=−2∫(1/((t−1)^2 −((√2))^2 ))=−2(1/(2(√2)))log(((t−1−(√2))/(t−1+(√2))))+C =(1/( (√2)))log(((t−1+(√2))/(t−1−(√2))))+C=(1/( (√2)))log(((tan(x/2)−1+(√2))/(tan(x/2)−1−(√2))))+C
$$\mathrm{2}\int\frac{\mathrm{1}}{\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}.\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:\:\:\:\:\left({tan}\frac{{x}}{\mathrm{2}}={t}\right)\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\:{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}=\frac{{dt}}{{dx}}\:,\:\:{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}=\mathrm{1}+{t}^{\mathrm{2}} \\ $$$$\mathrm{2}\int\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}{t}−{t}^{\mathrm{2}} } \\ $$$$−\mathrm{2}\int\frac{\mathrm{1}}{\left({t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}\right)−\mathrm{2}}=−\mathrm{2}\int\frac{\mathrm{1}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }=−\mathrm{2}\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{log}\left(\frac{{t}−\mathrm{1}−\sqrt{\mathrm{2}}}{{t}−\mathrm{1}+\sqrt{\mathrm{2}}}\right)+{C} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{log}\left(\frac{{t}−\mathrm{1}+\sqrt{\mathrm{2}}}{{t}−\mathrm{1}−\sqrt{\mathrm{2}}}\right)+{C}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{log}\left(\frac{{tan}\frac{{x}}{\mathrm{2}}−\mathrm{1}+\sqrt{\mathrm{2}}}{{tan}\frac{{x}}{\mathrm{2}}−\mathrm{1}−\sqrt{\mathrm{2}}}\right)+{C} \\ $$$$ \\ $$
Answered by Coronavirus last updated on 01/Aug/20
sinx+cosx=(√2)cos(x−(π/4)) (1/(cosa))=((cosa)/(cos^2 a))=((cosa)/(1−sin^2 a))=(((d(sina))/da)/(1−(sina)^2 ))=d(argth(sina))/da=((d((1/2)ln(((1+sina)/(1−sina)))))/da) yet ∫(1/(sin(x)+cos(x)))dx=(1/( (√2)))∫(1/(cos(x−(π/4)) ))dx =(1/( (√2)))argth(sin(x−(π/4)))+C =(1/(2(√2)))ln(((1+sin(x−(π/4)))/(1−sin(x−(π/4)))))+C so ∫(1/(sin(x)+cos(x)))dx=(1/(2(√2)))ln(((1+sin(x−(π/4)))/(1−sin(x−(π/4)))))+C
$${sinx}+{cosx}=\sqrt{\mathrm{2}}{cos}\left({x}−\frac{\pi}{\mathrm{4}}\right) \\ $$$$\frac{\mathrm{1}}{{cosa}}=\frac{{cosa}}{{cos}^{\mathrm{2}} {a}}=\frac{{cosa}}{\mathrm{1}−{sin}^{\mathrm{2}} {a}}=\frac{\frac{{d}\left({sina}\right)}{{da}}}{\mathrm{1}−\left({sina}\right)^{\mathrm{2}} }={d}\left({argth}\left({sina}\right)\right)/{da}=\frac{{d}\left(\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}+{sina}}{\mathrm{1}−{sina}}\right)\right)}{{da}}\:\: \\ $$$${yet}\:\int\frac{\mathrm{1}}{{sin}\left({x}\right)+{cos}\left({x}\right)}{dx}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{\mathrm{1}}{{cos}\left({x}−\frac{\pi}{\mathrm{4}}\right)\:\:\:}{dx}\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{argth}\left({sin}\left({x}−\frac{\pi}{\mathrm{4}}\right)\right)+{C} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\left(\frac{\mathrm{1}+{sin}\left({x}−\frac{\pi}{\mathrm{4}}\right)}{\mathrm{1}−{sin}\left({x}−\frac{\pi}{\mathrm{4}}\right)}\right)+{C} \\ $$$${so}\:\:\int\frac{\mathrm{1}}{\mathrm{sin}\left(\mathrm{x}\right)+\mathrm{cos}\left(\mathrm{x}\right)}\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\left(\frac{\mathrm{1}+\mathrm{sin}\left(\mathrm{x}−\frac{\pi}{\mathrm{4}}\right)}{\mathrm{1}−\mathrm{sin}\left(\mathrm{x}−\frac{\pi}{\mathrm{4}}\right)}\right)+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *