Question Number 105945 by Algoritm last updated on 01/Aug/20
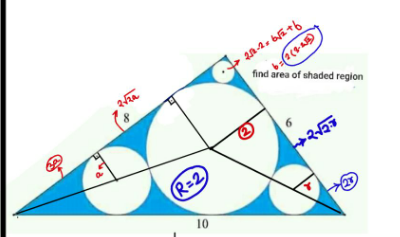
Answered by 1549442205PVT last updated on 02/Aug/20
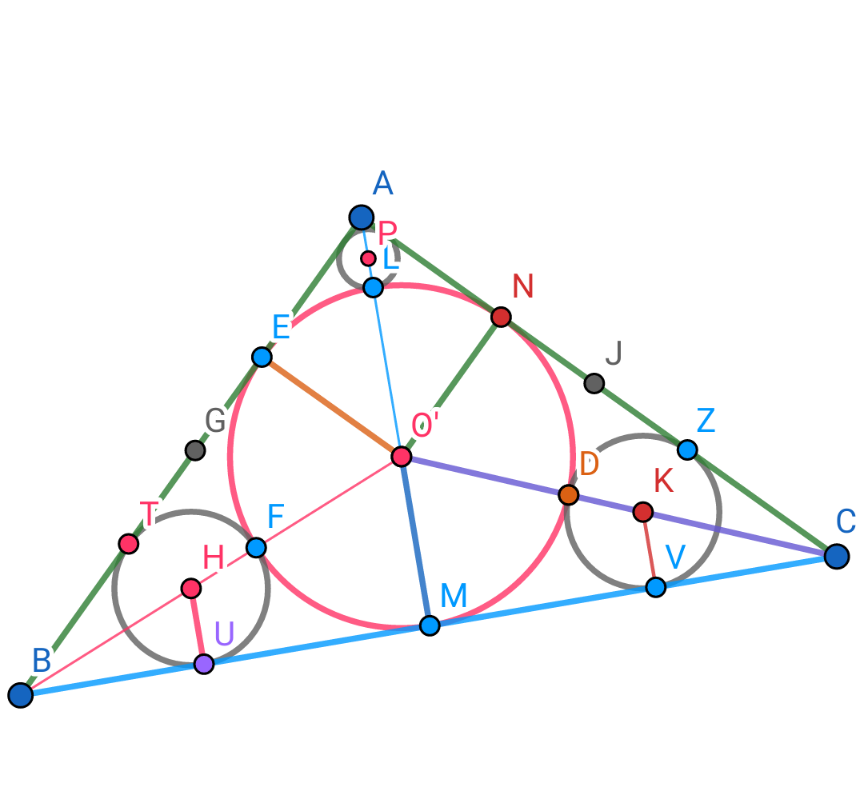
Commented by 1549442205PVT last updated on 02/Aug/20
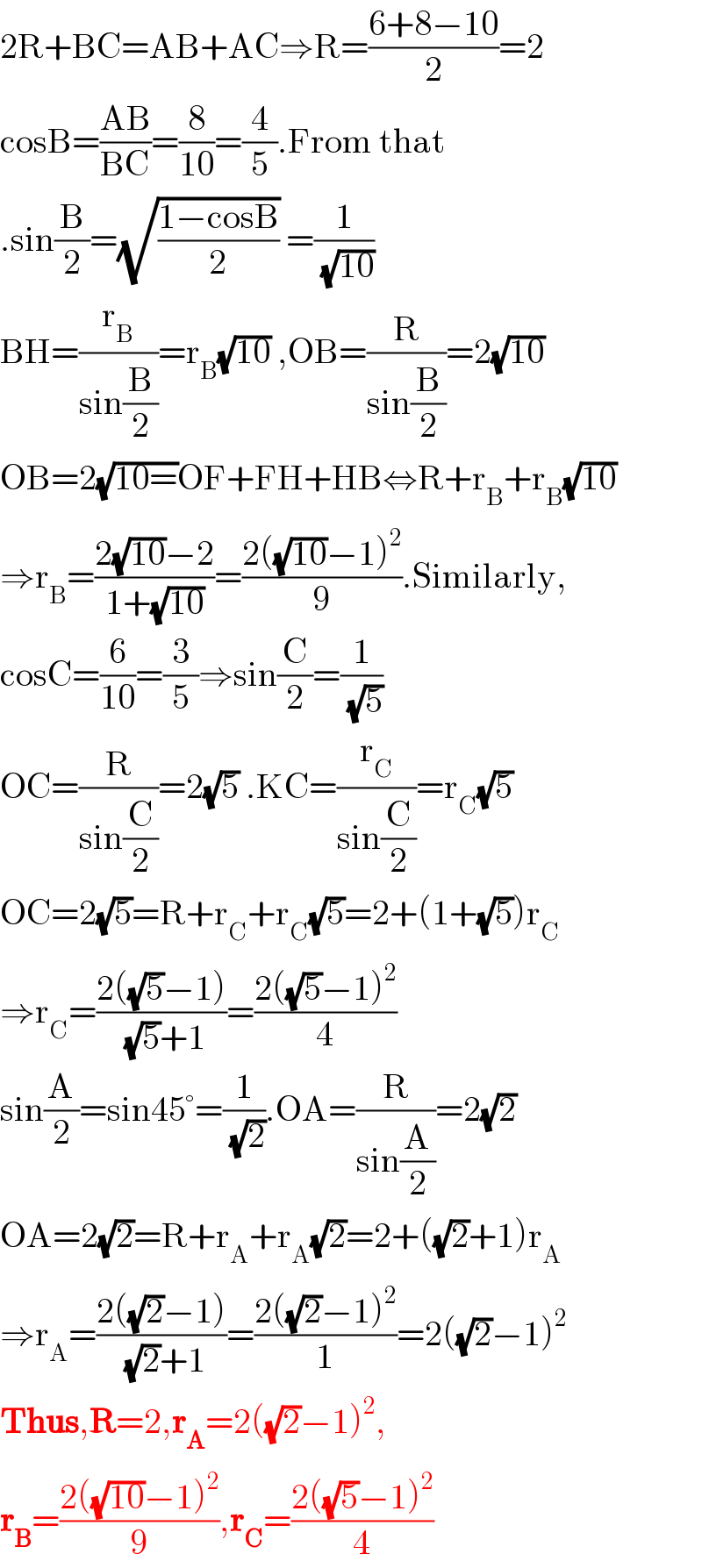
$$\mathrm{2R}+\mathrm{BC}=\mathrm{AB}+\mathrm{AC}\Rightarrow\mathrm{R}=\frac{\mathrm{6}+\mathrm{8}−\mathrm{10}}{\mathrm{2}}=\mathrm{2} \\ $$$$\mathrm{cosB}=\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{8}}{\mathrm{10}}=\frac{\mathrm{4}}{\mathrm{5}}.\mathrm{From}\:\mathrm{that}\: \\ $$$$.\mathrm{sin}\frac{\mathrm{B}}{\mathrm{2}}=\sqrt{\frac{\mathrm{1}−\mathrm{cosB}}{\mathrm{2}}}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{10}}} \\ $$$$\mathrm{BH}=\frac{\mathrm{r}_{\mathrm{B}} }{\mathrm{sin}\frac{\mathrm{B}}{\mathrm{2}}}=\mathrm{r}_{\mathrm{B}} \sqrt{\mathrm{10}}\:,\mathrm{OB}=\frac{\mathrm{R}}{\mathrm{sin}\frac{\mathrm{B}}{\mathrm{2}}}=\mathrm{2}\sqrt{\mathrm{10}} \\ $$$$\mathrm{OB}=\mathrm{2}\sqrt{\mathrm{10}=}\mathrm{OF}+\mathrm{FH}+\mathrm{HB}\Leftrightarrow\mathrm{R}+\mathrm{r}_{\mathrm{B}} +\mathrm{r}_{\mathrm{B}} \sqrt{\mathrm{10}} \\ $$$$\Rightarrow\mathrm{r}_{\mathrm{B}} =\frac{\mathrm{2}\sqrt{\mathrm{10}}−\mathrm{2}}{\mathrm{1}+\sqrt{\mathrm{10}}}=\frac{\mathrm{2}\left(\sqrt{\mathrm{10}}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{9}}.\mathrm{Similarly}, \\ $$$$\mathrm{cosC}=\frac{\mathrm{6}}{\mathrm{10}}=\frac{\mathrm{3}}{\mathrm{5}}\Rightarrow\mathrm{sin}\frac{\mathrm{C}}{\mathrm{2}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$$\mathrm{OC}=\frac{\mathrm{R}}{\mathrm{sin}\frac{\mathrm{C}}{\mathrm{2}}}=\mathrm{2}\sqrt{\mathrm{5}}\:.\mathrm{KC}=\frac{\mathrm{r}_{\mathrm{C}} }{\mathrm{sin}\frac{\mathrm{C}}{\mathrm{2}}}=\mathrm{r}_{\mathrm{C}} \sqrt{\mathrm{5}} \\ $$$$\mathrm{OC}=\mathrm{2}\sqrt{\mathrm{5}}=\mathrm{R}+\mathrm{r}_{\mathrm{C}} +\mathrm{r}_{\mathrm{C}} \sqrt{\mathrm{5}}=\mathrm{2}+\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)\mathrm{r}_{\mathrm{C}} \\ $$$$\Rightarrow\mathrm{r}_{\mathrm{C}} =\frac{\mathrm{2}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)}{\:\sqrt{\mathrm{5}}+\mathrm{1}}=\frac{\mathrm{2}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\mathrm{sin}\frac{\mathrm{A}}{\mathrm{2}}=\mathrm{sin45}°=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}.\mathrm{OA}=\frac{\mathrm{R}}{\mathrm{sin}\frac{\mathrm{A}}{\mathrm{2}}}=\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\mathrm{OA}=\mathrm{2}\sqrt{\mathrm{2}}=\mathrm{R}+\mathrm{r}_{\mathrm{A}} +\mathrm{r}_{\mathrm{A}} \sqrt{\mathrm{2}}=\mathrm{2}+\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)\mathrm{r}_{\mathrm{A}} \\ $$$$\Rightarrow\mathrm{r}_{\mathrm{A}} =\frac{\mathrm{2}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\:\sqrt{\mathrm{2}}+\mathrm{1}}=\frac{\mathrm{2}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{1}}=\mathrm{2}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{Thus}},\boldsymbol{\mathrm{R}}=\mathrm{2},\boldsymbol{\mathrm{r}}_{\boldsymbol{\mathrm{A}}} =\mathrm{2}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} , \\ $$$$\boldsymbol{\mathrm{r}}_{\boldsymbol{\mathrm{B}}} =\frac{\mathrm{2}\left(\sqrt{\mathrm{10}}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{9}},\boldsymbol{\mathrm{r}}_{\boldsymbol{\mathrm{C}}} =\frac{\mathrm{2}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$
Commented by Algoritm last updated on 02/Aug/20

$$\mathrm{thanks} \\ $$
