Question Number 105951 by Study last updated on 01/Aug/20

Answered by Dwaipayan Shikari last updated on 01/Aug/20
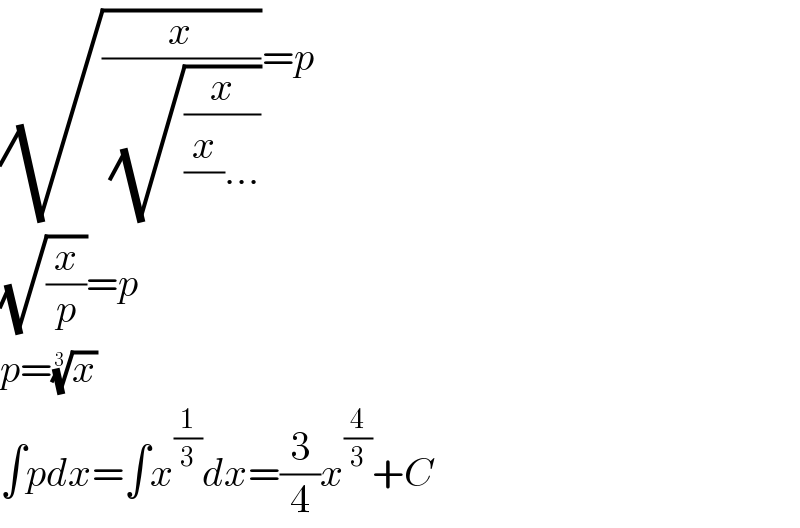
$$\sqrt{\frac{{x}}{\:\sqrt{\frac{{x}}{\frac{{x}}{}…}}}}={p} \\ $$$$\sqrt{\frac{{x}}{{p}}}={p} \\ $$$${p}=\sqrt[{\mathrm{3}}]{{x}} \\ $$$$\int{pdx}=\int{x}^{\frac{\mathrm{1}}{\mathrm{3}}} {dx}=\frac{\mathrm{3}}{\mathrm{4}}{x}^{\frac{\mathrm{4}}{\mathrm{3}}} +{C} \\ $$
Commented by malwaan last updated on 02/Aug/20
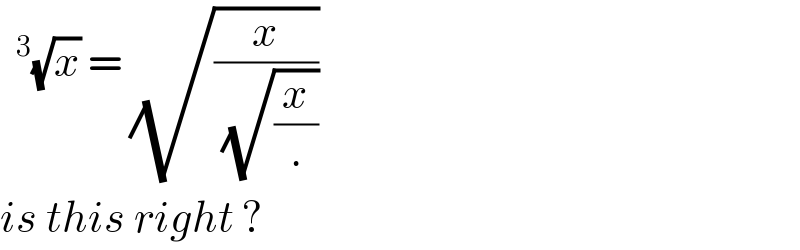
$$\sqrt{{x}}\:=\:\sqrt{\frac{{x}}{\:\sqrt{\frac{{x}}{.}}}}\: \\ $$$${is}\:{this}\:{right}\:? \\ $$
Commented by Her_Majesty last updated on 03/Aug/20

$${yes} \\ $$
Answered by Her_Majesty last updated on 01/Aug/20
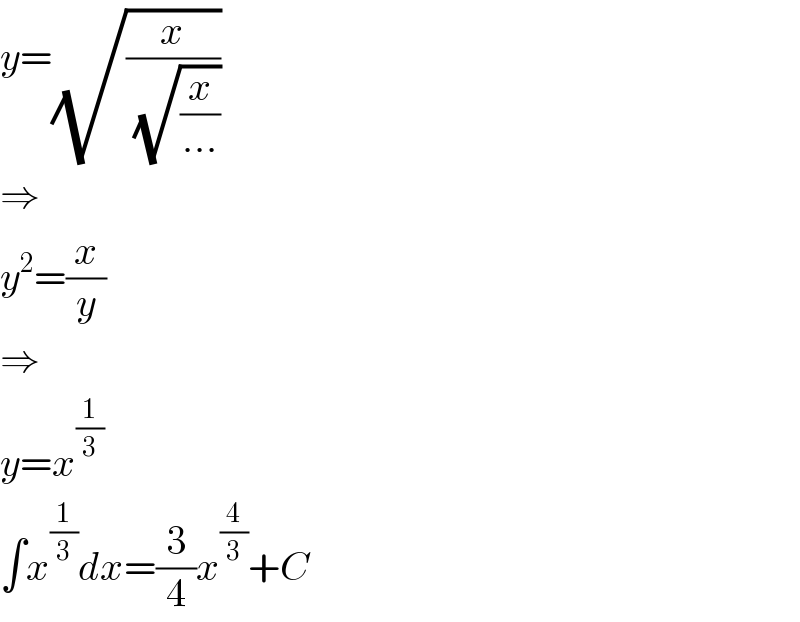
$${y}=\sqrt{\frac{{x}}{\:\sqrt{\frac{{x}}{…}}}} \\ $$$$\Rightarrow \\ $$$${y}^{\mathrm{2}} =\frac{{x}}{{y}} \\ $$$$\Rightarrow \\ $$$${y}={x}^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\int{x}^{\frac{\mathrm{1}}{\mathrm{3}}} {dx}=\frac{\mathrm{3}}{\mathrm{4}}{x}^{\frac{\mathrm{4}}{\mathrm{3}}} +{C} \\ $$
