Question Number 105952 by Study last updated on 01/Aug/20

Answered by Her_Majesty last updated on 01/Aug/20
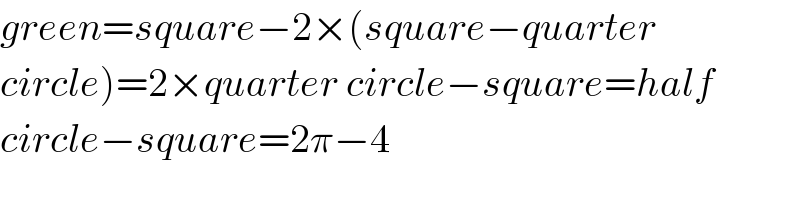
$${green}={square}−\mathrm{2}×\left({square}−{quarter}\right. \\ $$$$\left.{circle}\right)=\mathrm{2}×{quarter}\:{circle}−{square}={half} \\ $$$${circle}−{square}=\mathrm{2}\pi−\mathrm{4} \\ $$
Answered by 1549442205PVT last updated on 02/Aug/20
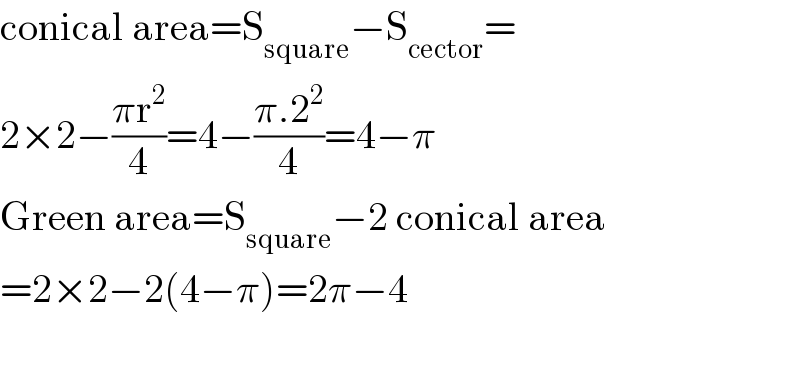
$$\mathrm{conical}\:\mathrm{area}=\mathrm{S}_{\mathrm{square}} −\mathrm{S}_{\mathrm{cector}} = \\ $$$$\mathrm{2}×\mathrm{2}−\frac{\pi\mathrm{r}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{4}−\frac{\pi.\mathrm{2}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{4}−\pi \\ $$$$\mathrm{Green}\:\mathrm{area}=\mathrm{S}_{\mathrm{square}} −\mathrm{2}\:\mathrm{conical}\:\mathrm{area} \\ $$$$=\mathrm{2}×\mathrm{2}−\mathrm{2}\left(\mathrm{4}−\pi\right)=\mathrm{2}\pi−\mathrm{4} \\ $$$$ \\ $$
