Question-106033

Question Number 106033 by mohammad17 last updated on 02/Aug/20

Answered by mathmax by abdo last updated on 02/Aug/20

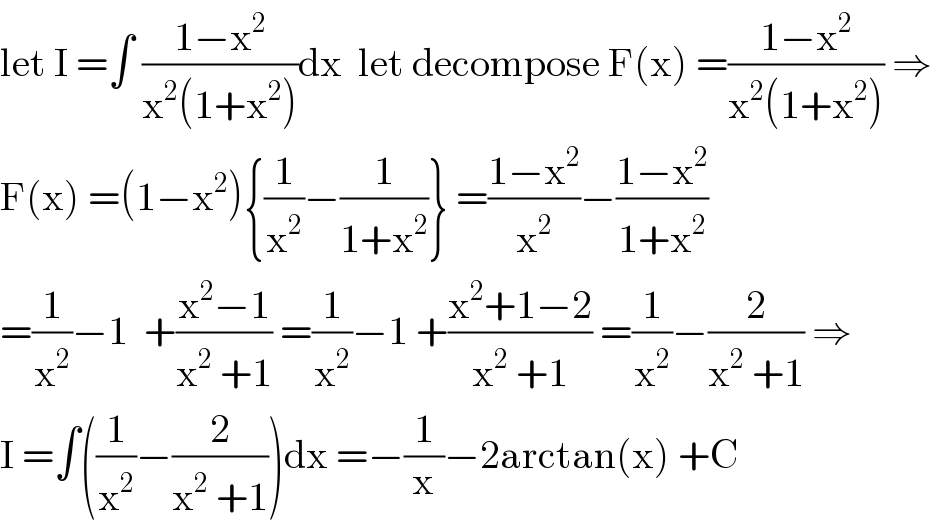
let I =∫ ((1−x^2 )/(x^2 (1+x^2 )))dx let decompose F(x) =((1−x^2 )/(x^2 (1+x^2 ))) ⇒ F(x) =(1−x^2 ){(1/x^2 )−(1/(1+x^2 ))} =((1−x^2 )/x^2 )−((1−x^2 )/(1+x^2 )) =(1/x^2 )−1 +((x^2 −1)/(x^2 +1)) =(1/x^2 )−1 +((x^2 +1−2)/(x^2 +1)) =(1/x^2 )−(2/(x^2 +1)) ⇒ I =∫((1/x^2 )−(2/(x^2 +1)))dx =−(1/x)−2arctan(x) +C

$$\mathrm{let}\:\mathrm{I}\:=\int\:\frac{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\mathrm{dx}\:\:\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{x}\right)\:=\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\left\{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right\}\:=\frac{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\mathrm{1}\:\:+\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\mathrm{1}\:+\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int\left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\right)\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{x}}−\mathrm{2arctan}\left(\mathrm{x}\right)\:+\mathrm{C} \\ $$

Answered by Dwaipayan Shikari last updated on 02/Aug/20

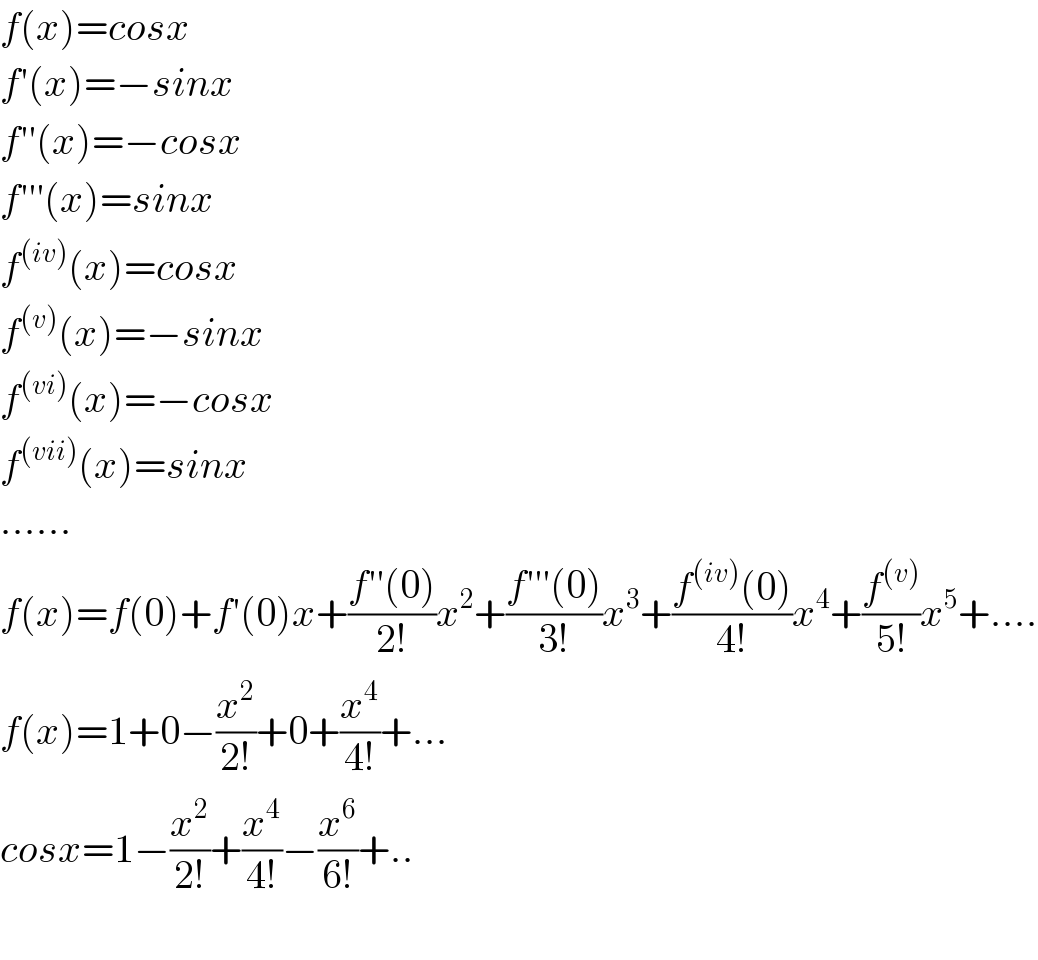
f(x)=cosx f′(x)=−sinx f′′(x)=−cosx f′′′(x)=sinx f^((iv)) (x)=cosx f^((v)) (x)=−sinx f^((vi)) (x)=−cosx f^((vii)) (x)=sinx ...... f(x)=f(0)+f′(0)x+((f′′(0))/(2!))x^2 +((f′′′(0))/(3!))x^3 +((f^((iv)) (0))/(4!))x^4 +(f^((v)) /(5!))x^5 +.... f(x)=1+0−(x^2 /(2!))+0+(x^4 /(4!))+... cosx=1−(x^2 /(2!))+(x^4 /(4!))−(x^6 /(6!))+..

$${f}\left({x}\right)={cosx} \\ $$$${f}'\left({x}\right)=−{sinx} \\ $$$${f}''\left({x}\right)=−{cosx} \\ $$$${f}'''\left({x}\right)={sinx} \\ $$$${f}^{\left({iv}\right)} \left({x}\right)={cosx} \\ $$$${f}^{\left({v}\right)} \left({x}\right)=−{sinx} \\ $$$${f}^{\left({vi}\right)} \left({x}\right)=−{cosx} \\ $$$${f}^{\left({vii}\right)} \left({x}\right)={sinx} \\ $$$$…… \\ $$$${f}\left({x}\right)={f}\left(\mathrm{0}\right)+{f}'\left(\mathrm{0}\right){x}+\frac{{f}''\left(\mathrm{0}\right)}{\mathrm{2}!}{x}^{\mathrm{2}} +\frac{{f}'''\left(\mathrm{0}\right)}{\mathrm{3}!}{x}^{\mathrm{3}} +\frac{{f}^{\left({iv}\right)} \left(\mathrm{0}\right)}{\mathrm{4}!}{x}^{\mathrm{4}} +\frac{{f}^{\left({v}\right)} }{\mathrm{5}!}{x}^{\mathrm{5}} +…. \\ $$$${f}\left({x}\right)=\mathrm{1}+\mathrm{0}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\mathrm{0}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}+… \\ $$$${cosx}=\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}−\frac{{x}^{\mathrm{6}} }{\mathrm{6}!}+.. \\ $$$$ \\ $$

Commented by mohammad17 last updated on 02/Aug/20

$${thank}\:{you}\:{sir} \\ $$

Answered by Dwaipayan Shikari last updated on 02/Aug/20

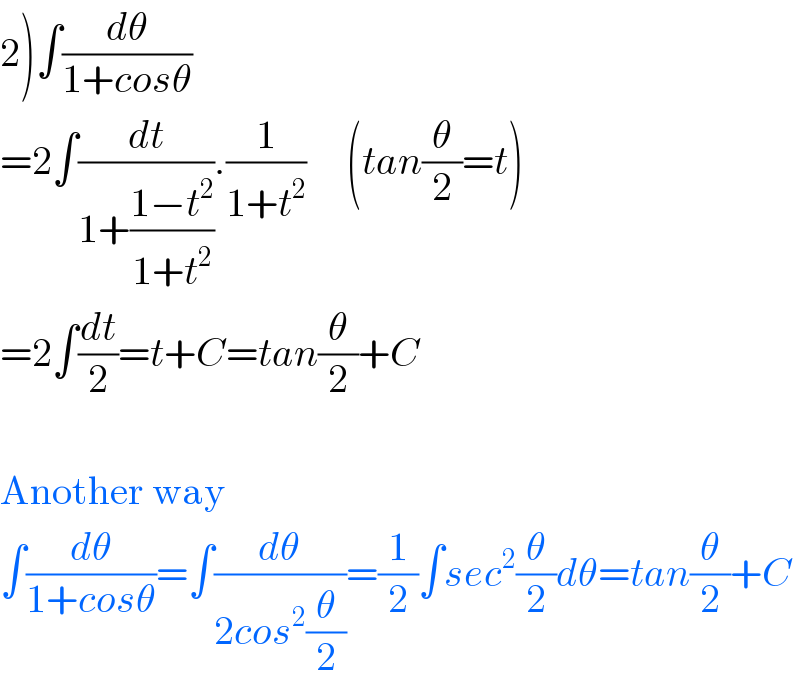
2)∫(dθ/(1+cosθ)) =2∫(dt/(1+((1−t^2 )/(1+t^2 )))).(1/(1+t^2 )) (tan(θ/2)=t) =2∫(dt/2)=t+C=tan(θ/2)+C Another way ∫(dθ/(1+cosθ))=∫(dθ/(2cos^2 (θ/2)))=(1/2)∫sec^2 (θ/2)dθ=tan(θ/2)+C

$$\left.\mathrm{2}\right)\int\frac{{d}\theta}{\mathrm{1}+{cos}\theta} \\ $$$$=\mathrm{2}\int\frac{{dt}}{\mathrm{1}+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}.\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\:\:\:\:\left({tan}\frac{\theta}{\mathrm{2}}={t}\right) \\ $$$$=\mathrm{2}\int\frac{{dt}}{\mathrm{2}}={t}+{C}={tan}\frac{\theta}{\mathrm{2}}+{C} \\ $$$$ \\ $$$$\mathrm{Another}\:\mathrm{way} \\ $$$$\int\frac{{d}\theta}{\mathrm{1}+{cos}\theta}=\int\frac{{d}\theta}{\mathrm{2}{cos}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}}=\frac{\mathrm{1}}{\mathrm{2}}\int{sec}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}{d}\theta={tan}\frac{\theta}{\mathrm{2}}+{C} \\ $$

Commented by mohammad17 last updated on 02/Aug/20

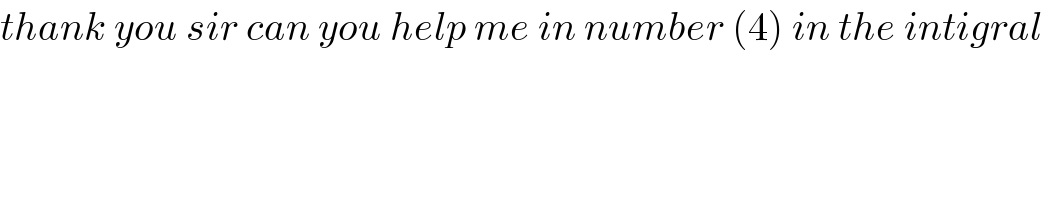
thank you sir can you help me in number (4) in the intigral

$${thank}\:{you}\:{sir}\:{can}\:{you}\:{help}\:{me}\:{in}\:{number}\:\left(\mathrm{4}\right)\:{in}\:{the}\:{intigral} \\ $$

Answered by Dwaipayan Shikari last updated on 02/Aug/20

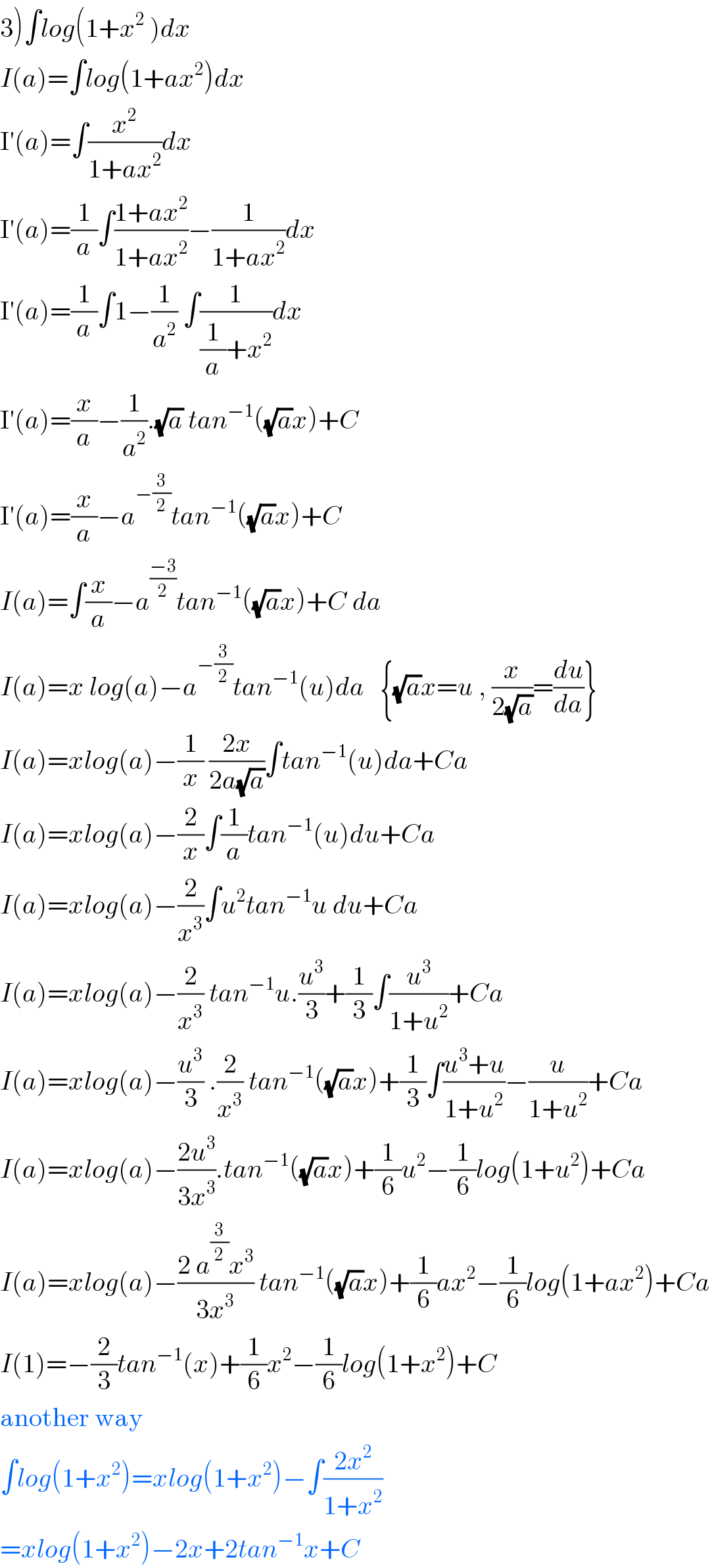
3)∫log(1+x^2 )dx I(a)=∫log(1+ax^2 )dx I′(a)=∫(x^2 /(1+ax^2 ))dx I′(a)=(1/a)∫((1+ax^2 )/(1+ax^2 ))−(1/(1+ax^2 ))dx I′(a)=(1/a)∫1−(1/a^2 ) ∫(1/((1/a)+x^2 ))dx I′(a)=(x/a)−(1/a^2 ).(√a) tan^(−1) ((√a)x)+C I′(a)=(x/a)−a^(−(3/2)) tan^(−1) ((√a)x)+C I(a)=∫(x/a)−a^((−3)/2) tan^(−1) ((√a)x)+C da I(a)=x log(a)−a^(−(3/2)) tan^(−1) (u)da {(√a)x=u , (x/(2(√a)))=(du/da)} I(a)=xlog(a)−(1/x) ((2x)/(2a(√a)))∫tan^(−1) (u)da+Ca I(a)=xlog(a)−(2/x)∫(1/a)tan^(−1) (u)du+Ca I(a)=xlog(a)−(2/x^3 )∫u^2 tan^(−1) u du+Ca I(a)=xlog(a)−(2/x^3 ) tan^(−1) u.(u^3 /3)+(1/3)∫(u^3 /(1+u^2 ))+Ca I(a)=xlog(a)−(u^3 /3) .(2/x^3 ) tan^(−1) ((√a)x)+(1/3)∫((u^3 +u)/(1+u^2 ))−(u/(1+u^2 ))+Ca I(a)=xlog(a)−((2u^3 )/(3x^3 )).tan^(−1) ((√a)x)+(1/6)u^2 −(1/6)log(1+u^2 )+Ca I(a)=xlog(a)−((2 a^(3/2) x^3 )/(3x^3 )) tan^(−1) ((√a)x)+(1/6)ax^2 −(1/6)log(1+ax^2 )+Ca I(1)=−(2/3)tan^(−1) (x)+(1/6)x^2 −(1/6)log(1+x^2 )+C another way ∫log(1+x^2 )=xlog(1+x^2 )−∫((2x^2 )/(1+x^2 )) =xlog(1+x^2 )−2x+2tan^(−1) x+C

$$\left.\mathrm{3}\right)\int{log}\left(\mathrm{1}+{x}^{\mathrm{2}} \:\right){dx} \\ $$$${I}\left({a}\right)=\int{log}\left(\mathrm{1}+{ax}^{\mathrm{2}} \right){dx} \\ $$$$\mathrm{I}'\left({a}\right)=\int\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{ax}^{\mathrm{2}} }{dx} \\ $$$$\mathrm{I}'\left({a}\right)=\frac{\mathrm{1}}{{a}}\int\frac{\mathrm{1}+{ax}^{\mathrm{2}} }{\mathrm{1}+{ax}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{1}+{ax}^{\mathrm{2}} }{dx} \\ $$$$\mathrm{I}'\left({a}\right)=\frac{\mathrm{1}}{{a}}\int\mathrm{1}−\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\:\int\frac{\mathrm{1}}{\frac{\mathrm{1}}{{a}}+{x}^{\mathrm{2}} }{dx} \\ $$$$\mathrm{I}'\left({a}\right)=\frac{{x}}{{a}}−\frac{\mathrm{1}}{{a}^{\mathrm{2}} }.\sqrt{{a}}\:{tan}^{−\mathrm{1}} \left(\sqrt{{a}}{x}\right)+{C} \\ $$$$\mathrm{I}'\left({a}\right)=\frac{{x}}{{a}}−{a}^{−\frac{\mathrm{3}}{\mathrm{2}}} {tan}^{−\mathrm{1}} \left(\sqrt{{a}}{x}\right)+{C} \\ $$$${I}\left({a}\right)=\int\frac{{x}}{{a}}−{a}^{\frac{−\mathrm{3}}{\mathrm{2}}} {tan}^{−\mathrm{1}} \left(\sqrt{{a}}{x}\right)+{C}\:{da} \\ $$$${I}\left({a}\right)={x}\:{log}\left({a}\right)−{a}^{−\frac{\mathrm{3}}{\mathrm{2}}} {tan}^{−\mathrm{1}} \left({u}\right){da}\:\:\:\left\{\sqrt{{a}}{x}={u}\:,\:\frac{{x}}{\mathrm{2}\sqrt{{a}}}=\frac{{du}}{{da}}\right\} \\ $$$${I}\left({a}\right)={xlog}\left({a}\right)−\frac{\mathrm{1}}{{x}}\:\frac{\mathrm{2}{x}}{\mathrm{2}{a}\sqrt{{a}}}\int{tan}^{−\mathrm{1}} \left({u}\right){da}+{Ca} \\ $$$${I}\left({a}\right)={xlog}\left({a}\right)−\frac{\mathrm{2}}{{x}}\int\frac{\mathrm{1}}{{a}}{tan}^{−\mathrm{1}} \left({u}\right){du}+{Ca} \\ $$$${I}\left({a}\right)={xlog}\left({a}\right)−\frac{\mathrm{2}}{{x}^{\mathrm{3}} }\int{u}^{\mathrm{2}} {tan}^{−\mathrm{1}} {u}\:{du}+{Ca} \\ $$$${I}\left({a}\right)={xlog}\left({a}\right)−\frac{\mathrm{2}}{{x}^{\mathrm{3}} }\:{tan}^{−\mathrm{1}} {u}.\frac{{u}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{u}^{\mathrm{3}} }{\mathrm{1}+{u}^{\mathrm{2}} }+{Ca} \\ $$$${I}\left({a}\right)={xlog}\left({a}\right)−\frac{{u}^{\mathrm{3}} }{\mathrm{3}}\:.\frac{\mathrm{2}}{{x}^{\mathrm{3}} }\:{tan}^{−\mathrm{1}} \left(\sqrt{{a}}{x}\right)+\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{u}^{\mathrm{3}} +{u}}{\mathrm{1}+{u}^{\mathrm{2}} }−\frac{{u}}{\mathrm{1}+{u}^{\mathrm{2}} }+{Ca} \\ $$$${I}\left({a}\right)={xlog}\left({a}\right)−\frac{\mathrm{2}{u}^{\mathrm{3}} }{\mathrm{3}{x}^{\mathrm{3}} }.{tan}^{−\mathrm{1}} \left(\sqrt{{a}}{x}\right)+\frac{\mathrm{1}}{\mathrm{6}}{u}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{6}}{log}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)+{Ca} \\ $$$${I}\left({a}\right)={xlog}\left({a}\right)−\frac{\mathrm{2}\:{a}^{\frac{\mathrm{3}}{\mathrm{2}}} {x}^{\mathrm{3}} }{\mathrm{3}{x}^{\mathrm{3}} }\:{tan}^{−\mathrm{1}} \left(\sqrt{{a}}{x}\right)+\frac{\mathrm{1}}{\mathrm{6}}{ax}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{6}}{log}\left(\mathrm{1}+{ax}^{\mathrm{2}} \right)+{Ca} \\ $$$${I}\left(\mathrm{1}\right)=−\frac{\mathrm{2}}{\mathrm{3}}{tan}^{−\mathrm{1}} \left({x}\right)+\frac{\mathrm{1}}{\mathrm{6}}{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{6}}{log}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)+{C} \\ $$$$\mathrm{another}\:\mathrm{way} \\ $$$$\int{log}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)={xlog}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−\int\frac{\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$={xlog}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−\mathrm{2}{x}+\mathrm{2}{tan}^{−\mathrm{1}} {x}+{C} \\ $$

Commented by mohammad17 last updated on 02/Aug/20

$${thank}\:{you}\:{sir}\: \\ $$

Answered by Dwaipayan Shikari last updated on 02/Aug/20

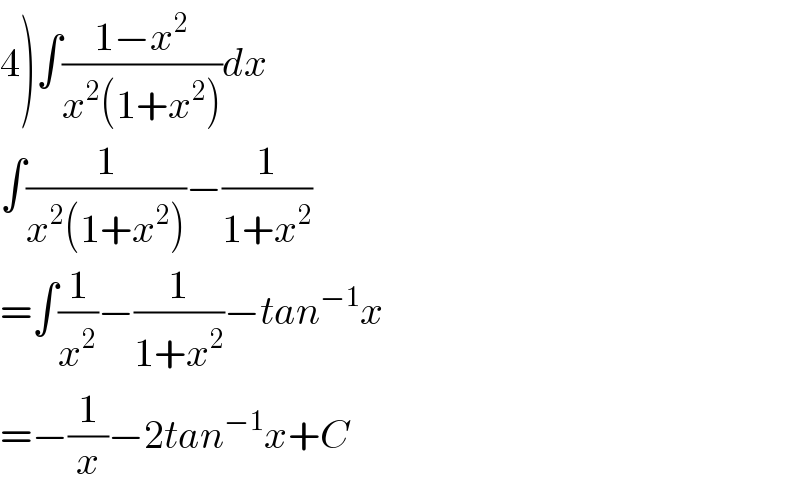
4)∫((1−x^2 )/(x^2 (1+x^2 )))dx ∫(1/(x^2 (1+x^2 )))−(1/(1+x^2 )) =∫(1/x^2 )−(1/(1+x^2 ))−tan^(−1) x =−(1/x)−2tan^(−1) x+C

$$\left.\mathrm{4}\right)\int\frac{\mathrm{1}−{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} \left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx} \\ $$$$\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} \left(\mathrm{1}+{x}^{\mathrm{2}} \right)}−\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$=\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }−{tan}^{−\mathrm{1}} {x} \\ $$$$=−\frac{\mathrm{1}}{{x}}−\mathrm{2}{tan}^{−\mathrm{1}} {x}+{C} \\ $$

Answered by bemath last updated on 02/Aug/20

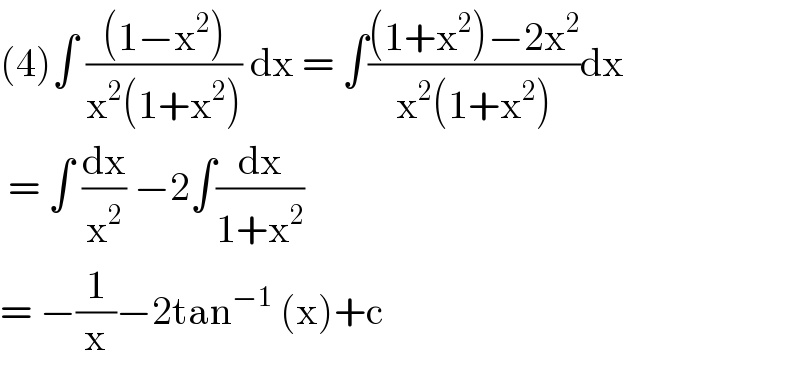
(4)∫ (((1−x^2 ))/(x^2 (1+x^2 ))) dx = ∫(((1+x^2 )−2x^2 )/(x^2 (1+x^2 )))dx = ∫ (dx/x^2 ) −2∫(dx/(1+x^2 )) = −(1/x)−2tan^(−1) (x)+c

$$\left(\mathrm{4}\right)\int\:\frac{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\:\mathrm{dx}\:=\:\int\frac{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)−\mathrm{2x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\mathrm{dx} \\ $$$$\:=\:\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} }\:−\mathrm{2}\int\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{x}}−\mathrm{2tan}^{−\mathrm{1}} \:\left(\mathrm{x}\right)+\mathrm{c}\: \\ $$

Commented by mohammad17 last updated on 02/Aug/20

$${thank}\:{you}\:{sir} \\ $$

Answered by mathmax by abdo last updated on 02/Aug/20

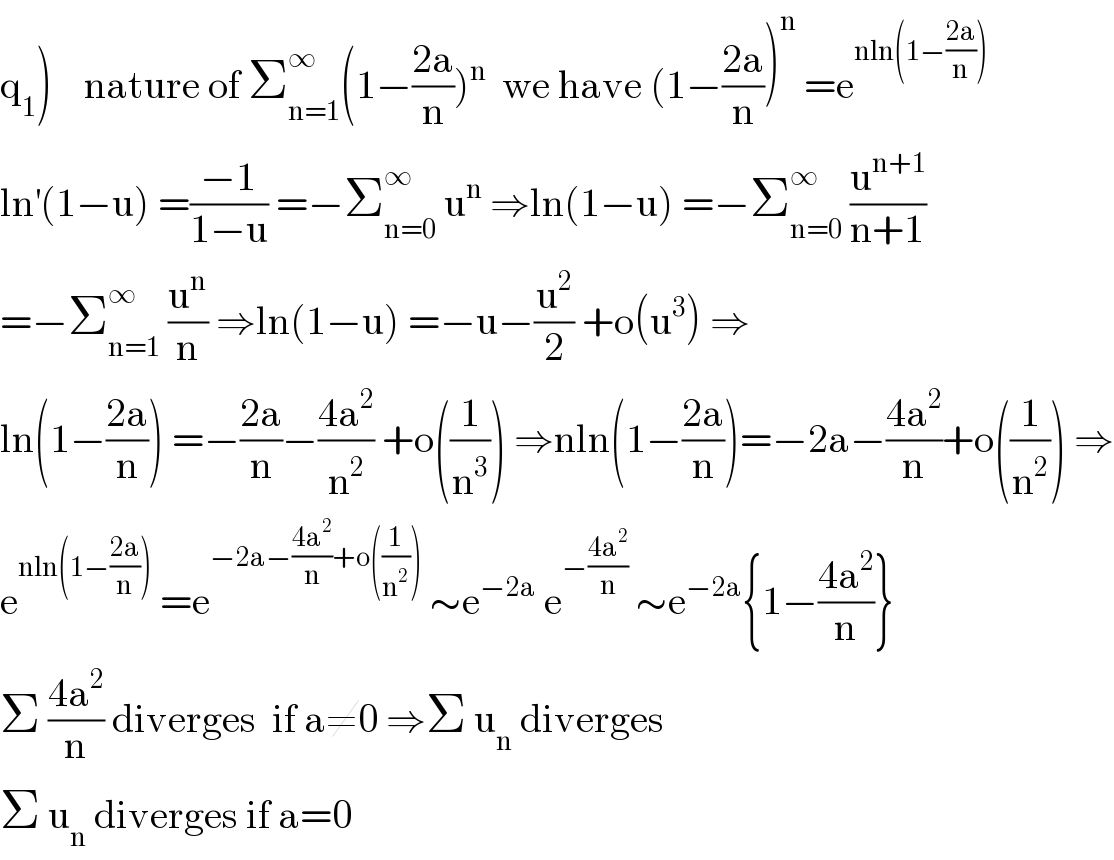
q_1 ) nature of Σ_(n=1) ^∞ (1−((2a)/n))^n we have (1−((2a)/n))^n =e^(nln(1−((2a)/n))) ln^′ (1−u) =((−1)/(1−u)) =−Σ_(n=0) ^∞ u^n ⇒ln(1−u) =−Σ_(n=0) ^∞ (u^(n+1) /(n+1)) =−Σ_(n=1) ^∞ (u^n /n) ⇒ln(1−u) =−u−(u^2 /2) +o(u^3 ) ⇒ ln(1−((2a)/n)) =−((2a)/n)−((4a^2 )/n^2 ) +o((1/n^3 )) ⇒nln(1−((2a)/n))=−2a−((4a^2 )/n)+o((1/n^2 )) ⇒ e^(nln(1−((2a)/n))) =e^(−2a−((4a^2 )/n)+o((1/n^2 ))) ∼e^(−2a) e^(−((4a^2 )/n)) ∼e^(−2a) {1−((4a^2 )/n)} Σ ((4a^2 )/n) diverges if a≠0 ⇒Σ u_n diverges Σ u_n diverges if a=0

$$\left.\mathrm{q}_{\mathrm{1}} \right)\:\:\:\:\mathrm{nature}\:\mathrm{of}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \left(\mathrm{1}−\frac{\mathrm{2a}}{\mathrm{n}}\right)^{\mathrm{n}} \:\:\mathrm{we}\:\mathrm{have}\:\left(\mathrm{1}−\frac{\mathrm{2a}}{\mathrm{n}}\right)^{\mathrm{n}} \:=\mathrm{e}^{\mathrm{nln}\left(\mathrm{1}−\frac{\mathrm{2a}}{\mathrm{n}}\right)} \\ $$$$\mathrm{ln}^{'} \left(\mathrm{1}−\mathrm{u}\right)\:=\frac{−\mathrm{1}}{\mathrm{1}−\mathrm{u}}\:=−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{u}^{\mathrm{n}} \:\Rightarrow\mathrm{ln}\left(\mathrm{1}−\mathrm{u}\right)\:=−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{u}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}} \\ $$$$=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{u}^{\mathrm{n}} }{\mathrm{n}}\:\Rightarrow\mathrm{ln}\left(\mathrm{1}−\mathrm{u}\right)\:=−\mathrm{u}−\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{2}}\:+\mathrm{o}\left(\mathrm{u}^{\mathrm{3}} \right)\:\Rightarrow \\ $$$$\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{2a}}{\mathrm{n}}\right)\:=−\frac{\mathrm{2a}}{\mathrm{n}}−\frac{\mathrm{4a}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }\:+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }\right)\:\Rightarrow\mathrm{nln}\left(\mathrm{1}−\frac{\mathrm{2a}}{\mathrm{n}}\right)=−\mathrm{2a}−\frac{\mathrm{4a}^{\mathrm{2}} }{\mathrm{n}}+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\right)\:\Rightarrow \\ $$$$\mathrm{e}^{\mathrm{nln}\left(\mathrm{1}−\frac{\mathrm{2a}}{\mathrm{n}}\right)} \:=\mathrm{e}^{−\mathrm{2a}−\frac{\mathrm{4a}^{\mathrm{2}} }{\mathrm{n}}+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\right)} \:\sim\mathrm{e}^{−\mathrm{2a}} \:\mathrm{e}^{−\frac{\mathrm{4a}^{\mathrm{2}} }{\mathrm{n}}} \:\sim\mathrm{e}^{−\mathrm{2a}} \left\{\mathrm{1}−\frac{\mathrm{4a}^{\mathrm{2}} }{\mathrm{n}}\right\} \\ $$$$\Sigma\:\frac{\mathrm{4a}^{\mathrm{2}} }{\mathrm{n}}\:\mathrm{diverges}\:\:\mathrm{if}\:\mathrm{a}\neq\mathrm{0}\:\Rightarrow\Sigma\:\mathrm{u}_{\mathrm{n}} \:\mathrm{diverges} \\ $$$$\Sigma\:\mathrm{u}_{\mathrm{n}} \:\mathrm{diverges}\:\mathrm{if}\:\mathrm{a}=\mathrm{0} \\ $$

Commented by mohammad17 last updated on 02/Aug/20

$${thank}\:{you}\:{sir} \\ $$

Commented by abdomathmax last updated on 02/Aug/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$

Answered by bemath last updated on 02/Aug/20

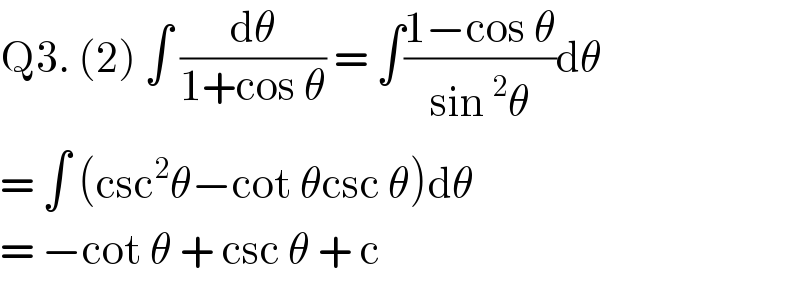
Q3. (2) ∫ (dθ/(1+cos θ)) = ∫((1−cos θ)/(sin^2 θ))dθ = ∫ (csc^2 θ−cot θcsc θ)dθ = −cot θ + csc θ + c

$$\mathrm{Q3}.\:\left(\mathrm{2}\right)\:\int\:\frac{\mathrm{d}\theta}{\mathrm{1}+\mathrm{cos}\:\theta}\:=\:\int\frac{\mathrm{1}−\mathrm{cos}\:\theta}{\mathrm{sin}\:^{\mathrm{2}} \theta}\mathrm{d}\theta \\ $$$$=\:\int\:\left(\mathrm{csc}^{\mathrm{2}} \theta−\mathrm{cot}\:\theta\mathrm{csc}\:\theta\right)\mathrm{d}\theta \\ $$$$=\:−\mathrm{cot}\:\theta\:+\:\mathrm{csc}\:\theta\:+\:\mathrm{c}\: \\ $$

Commented by mohammad17 last updated on 02/Aug/20

$${thank}\:{you}\:{sir} \\ $$

Answered by mathmax by abdo last updated on 02/Aug/20

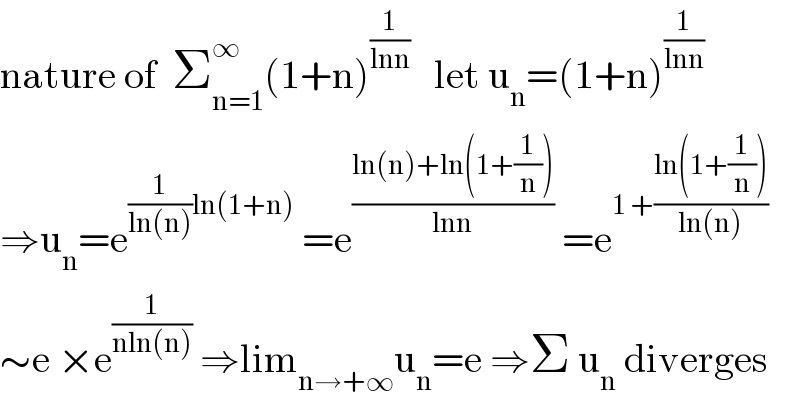
nature of Σ_(n=1) ^∞ (1+n)^(1/(lnn)) let u_n =(1+n)^(1/(lnn)) ⇒u_n =e^((1/(ln(n)))ln(1+n)) =e^((ln(n)+ln(1+(1/n)))/(lnn)) =e^(1 +((ln(1+(1/n)))/(ln(n)))) ∼e ×e^(1/(nln(n))) ⇒lim_(n→+∞) u_n =e ⇒Σ u_n diverges

$$\mathrm{nature}\:\mathrm{of}\:\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \left(\mathrm{1}+\mathrm{n}\right)^{\frac{\mathrm{1}}{\mathrm{lnn}}} \:\:\:\mathrm{let}\:\mathrm{u}_{\mathrm{n}} =\left(\mathrm{1}+\mathrm{n}\right)^{\frac{\mathrm{1}}{\mathrm{lnn}}} \\ $$$$\Rightarrow\mathrm{u}_{\mathrm{n}} =\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{ln}\left(\mathrm{n}\right)}\mathrm{ln}\left(\mathrm{1}+\mathrm{n}\right)} \:=\mathrm{e}^{\frac{\mathrm{ln}\left(\mathrm{n}\right)+\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\right)}{\mathrm{lnn}}} \:=\mathrm{e}^{\mathrm{1}\:+\frac{\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\right)}{\mathrm{ln}\left(\mathrm{n}\right)}} \\ $$$$\sim\mathrm{e}\:×\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{nln}\left(\mathrm{n}\right)}} \:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{u}_{\mathrm{n}} =\mathrm{e}\:\Rightarrow\Sigma\:\mathrm{u}_{\mathrm{n}} \:\mathrm{diverges} \\ $$

Commented by mohammad17 last updated on 02/Aug/20

$${thank}\:{you}\:{sir} \\ $$

Answered by mathmax by abdo last updated on 02/Aug/20

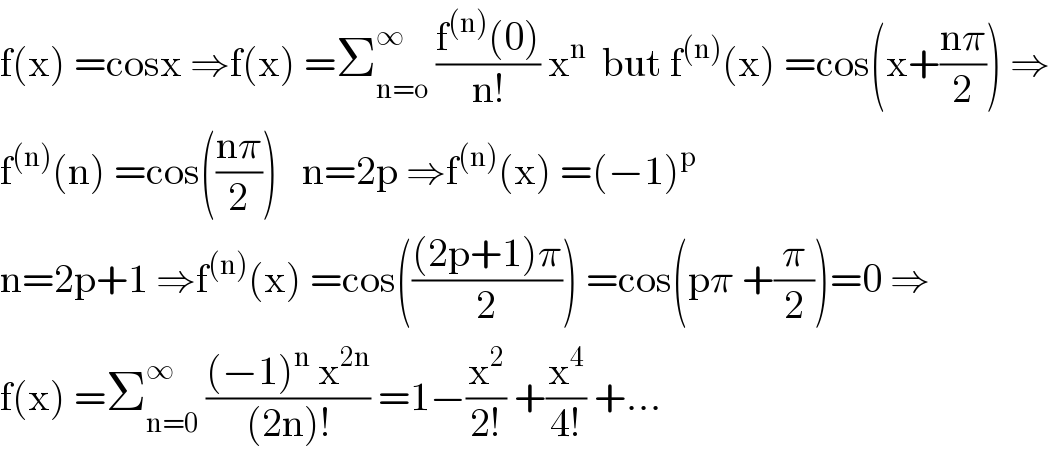
f(x) =cosx ⇒f(x) =Σ_(n=o) ^∞ ((f^((n)) (0))/(n!)) x^n but f^((n)) (x) =cos(x+((nπ)/2)) ⇒ f^((n)) (n) =cos(((nπ)/2)) n=2p ⇒f^((n)) (x) =(−1)^p n=2p+1 ⇒f^((n)) (x) =cos((((2p+1)π)/2)) =cos(pπ +(π/2))=0 ⇒ f(x) =Σ_(n=0) ^∞ (((−1)^n x^(2n) )/((2n)!)) =1−(x^2 /(2!)) +(x^4 /(4!)) +...

$$\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{cosx}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\sum_{\mathrm{n}=\mathrm{o}} ^{\infty} \:\frac{\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right)}{\mathrm{n}!}\:\mathrm{x}^{\mathrm{n}} \:\:\mathrm{but}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)\:=\mathrm{cos}\left(\mathrm{x}+\frac{\mathrm{n}\pi}{\mathrm{2}}\right)\:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{n}\right)\:=\mathrm{cos}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right)\:\:\:\mathrm{n}=\mathrm{2p}\:\Rightarrow\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)\:=\left(−\mathrm{1}\right)^{\mathrm{p}} \\ $$$$\mathrm{n}=\mathrm{2p}+\mathrm{1}\:\Rightarrow\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)\:=\mathrm{cos}\left(\frac{\left(\mathrm{2p}+\mathrm{1}\right)\pi}{\mathrm{2}}\right)\:=\mathrm{cos}\left(\mathrm{p}\pi\:+\frac{\pi}{\mathrm{2}}\right)=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{2n}} }{\left(\mathrm{2n}\right)!}\:=\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}!}\:+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{4}!}\:+… \\ $$

Commented by mohammad17 last updated on 02/Aug/20

$${thank}\:{you}\:{sir} \\ $$

Answered by mathmax by abdo last updated on 02/Aug/20

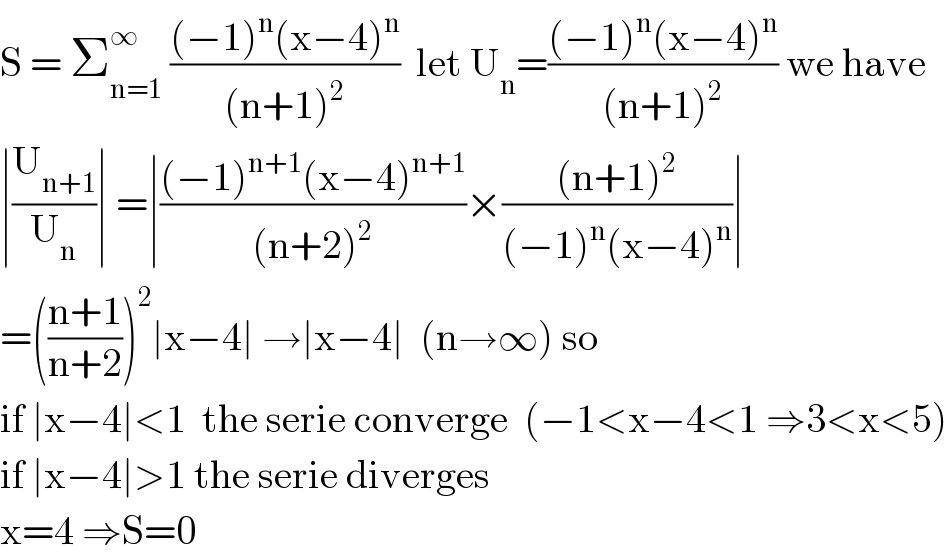
S = Σ_(n=1) ^∞ (((−1)^n (x−4)^n )/((n+1)^2 )) let U_n =(((−1)^n (x−4)^n )/((n+1)^2 )) we have ∣(U_(n+1) /U_n )∣ =∣(((−1)^(n+1) (x−4)^(n+1) )/((n+2)^2 ))×(((n+1)^2 )/((−1)^n (x−4)^n ))∣ =(((n+1)/(n+2)))^2 ∣x−4∣ →∣x−4∣ (n→∞) so if ∣x−4∣<1 the serie converge (−1<x−4<1 ⇒3<x<5) if ∣x−4∣>1 the serie diverges x=4 ⇒S=0

$$\mathrm{S}\:=\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\mathrm{x}−\mathrm{4}\right)^{\mathrm{n}} }{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\:\mathrm{let}\:\mathrm{U}_{\mathrm{n}} =\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\mathrm{x}−\mathrm{4}\right)^{\mathrm{n}} }{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{we}\:\mathrm{have} \\ $$$$\mid\frac{\mathrm{U}_{\mathrm{n}+\mathrm{1}} }{\mathrm{U}_{\mathrm{n}} }\mid\:=\mid\frac{\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} \left(\mathrm{x}−\mathrm{4}\right)^{\mathrm{n}+\mathrm{1}} }{\left(\mathrm{n}+\mathrm{2}\right)^{\mathrm{2}} }×\frac{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }{\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\mathrm{x}−\mathrm{4}\right)^{\mathrm{n}} }\mid \\ $$$$=\left(\frac{\mathrm{n}+\mathrm{1}}{\mathrm{n}+\mathrm{2}}\right)^{\mathrm{2}} \mid\mathrm{x}−\mathrm{4}\mid\:\rightarrow\mid\mathrm{x}−\mathrm{4}\mid\:\:\left(\mathrm{n}\rightarrow\infty\right)\:\mathrm{so} \\ $$$$\mathrm{if}\:\mid\mathrm{x}−\mathrm{4}\mid<\mathrm{1}\:\:\mathrm{the}\:\mathrm{serie}\:\mathrm{converge}\:\:\left(−\mathrm{1}<\mathrm{x}−\mathrm{4}<\mathrm{1}\:\Rightarrow\mathrm{3}<\mathrm{x}<\mathrm{5}\right) \\ $$$$\mathrm{if}\:\mid\mathrm{x}−\mathrm{4}\mid>\mathrm{1}\:\mathrm{the}\:\mathrm{serie}\:\mathrm{diverges} \\ $$$$\mathrm{x}=\mathrm{4}\:\Rightarrow\mathrm{S}=\mathrm{0}\: \\ $$

Commented by mohammad17 last updated on 02/Aug/20

$${thank}\:{you}\:{sir} \\ $$

Answered by mathmax by abdo last updated on 02/Aug/20

convergence of Σ_(n=1) ^∞ (((2n+1)(x−2)^n )/n^3 ) let v_n =(((2n+1)(x−2)^n )/n^3 ) we have ∣(v_(n+1) /v_n )∣ =∣(((2n+3)(x−2)^(n+1) )/((n+1)^3 ))×(n^3 /((2n+1)(x−2)^n ))∣ =((n/(n+1)))^3 ((2n+3)/(2n+1)) ×∣x−2∣ →∣x−2∣ so if ∣x−2∣<1 ⇒Σ v_n converge(−1<x−2<1 ⇒1<x<3 ⇒D_c =]1,3[) if ∣x−2∣>1 ⇒Σ v_n diverges x=2 ⇒Σ v_n =0

$$\mathrm{convergence}\:\mathrm{of}\:\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(\mathrm{2n}+\mathrm{1}\right)\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{3}} }\:\:\mathrm{let}\:\mathrm{v}_{\mathrm{n}} =\frac{\left(\mathrm{2n}+\mathrm{1}\right)\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{3}} } \\ $$$$\mathrm{we}\:\mathrm{have}\:\mid\frac{\mathrm{v}_{\mathrm{n}+\mathrm{1}} }{\mathrm{v}_{\mathrm{n}} }\mid\:=\mid\frac{\left(\mathrm{2n}+\mathrm{3}\right)\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{n}+\mathrm{1}} }{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{3}} }×\frac{\mathrm{n}^{\mathrm{3}} }{\left(\mathrm{2n}+\mathrm{1}\right)\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{n}} }\mid \\ $$$$=\left(\frac{\mathrm{n}}{\mathrm{n}+\mathrm{1}}\right)^{\mathrm{3}} \frac{\mathrm{2n}+\mathrm{3}}{\mathrm{2n}+\mathrm{1}}\:×\mid\mathrm{x}−\mathrm{2}\mid\:\rightarrow\mid\mathrm{x}−\mathrm{2}\mid\:\mathrm{so} \\ $$$$\mathrm{if}\:\mid\mathrm{x}−\mathrm{2}\mid<\mathrm{1}\:\Rightarrow\Sigma\:\mathrm{v}_{\mathrm{n}} \mathrm{converge}\left(−\mathrm{1}<\mathrm{x}−\mathrm{2}<\mathrm{1}\:\Rightarrow\mathrm{1}<\mathrm{x}<\mathrm{3}\:\Rightarrow\mathrm{D}_{\mathrm{c}} =\right]\mathrm{1},\mathrm{3}\left[\right) \\ $$$$\mathrm{if}\:\mid\mathrm{x}−\mathrm{2}\mid>\mathrm{1}\:\:\Rightarrow\Sigma\:\mathrm{v}_{\mathrm{n}} \:\mathrm{diverges} \\ $$$$\mathrm{x}=\mathrm{2}\:\Rightarrow\Sigma\:\mathrm{v}_{\mathrm{n}} =\mathrm{0} \\ $$$$ \\ $$$$ \\ $$

Commented by mohammad17 last updated on 02/Aug/20

$${thank}\:{you}\:{sir}\: \\ $$

Answered by mathmax by abdo last updated on 02/Aug/20

∫ (dθ/(1+cosθ)) =_(tan((θ/2))=t) ∫ ((2dt)/((1+t^2 )(1+((1−t^2 )/(1+t^2 ))))) =∫ ((2dt)/(1+t^2 +1−t^2 )) =∫ dt =tan((θ/2))+C ∫ ln(1+x^2 )dx =_(by parts) xln(1+x^2 )−∫ x.((2x)/(1+x^2 ))dx =xln(1+x^2 )−2 ∫((x^2 +1−1)/(1+x^2 ))dx =xln(1+x^2 )−2x+2arctanx+ C

$$\int\:\frac{\mathrm{d}\theta}{\mathrm{1}+\mathrm{cos}\theta}\:=_{\mathrm{tan}\left(\frac{\theta}{\mathrm{2}}\right)=\mathrm{t}} \:\:\:\int\:\:\frac{\mathrm{2dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\mathrm{1}+\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)}\:=\int\:\frac{\mathrm{2dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}−\mathrm{t}^{\mathrm{2}} } \\ $$$$=\int\:\mathrm{dt}\:=\mathrm{tan}\left(\frac{\theta}{\mathrm{2}}\right)+\mathrm{C} \\ $$$$\int\:\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx}\:=_{\mathrm{by}\:\mathrm{parts}} \:\:\:\mathrm{xln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)−\int\:\mathrm{x}.\frac{\mathrm{2x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\mathrm{xln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)−\mathrm{2}\:\int\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\mathrm{xln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)−\mathrm{2x}+\mathrm{2arctanx}+\:\mathrm{C} \\ $$$$ \\ $$

Commented by mohammad17 last updated on 02/Aug/20

$${thank}\:{you}\:{sir} \\ $$

Answered by mathmax by abdo last updated on 02/Aug/20

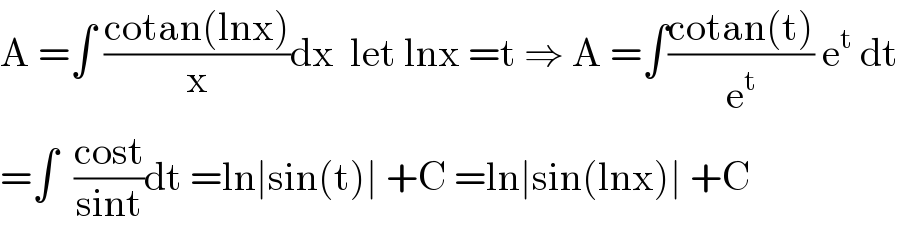
A =∫ ((cotan(lnx))/x)dx let lnx =t ⇒ A =∫((cotan(t))/e^t ) e^t dt =∫ ((cost)/(sint))dt =ln∣sin(t)∣ +C =ln∣sin(lnx)∣ +C

$$\mathrm{A}\:=\int\:\frac{\mathrm{cotan}\left(\mathrm{lnx}\right)}{\mathrm{x}}\mathrm{dx}\:\:\mathrm{let}\:\mathrm{lnx}\:=\mathrm{t}\:\Rightarrow\:\mathrm{A}\:=\int\frac{\mathrm{cotan}\left(\mathrm{t}\right)}{\mathrm{e}^{\mathrm{t}} }\:\mathrm{e}^{\mathrm{t}} \:\mathrm{dt} \\ $$$$=\int\:\:\frac{\mathrm{cost}}{\mathrm{sint}}\mathrm{dt}\:=\mathrm{ln}\mid\mathrm{sin}\left(\mathrm{t}\right)\mid\:+\mathrm{C}\:=\mathrm{ln}\mid\mathrm{sin}\left(\mathrm{lnx}\right)\mid\:+\mathrm{C} \\ $$

Answered by mathmax by abdo last updated on 02/Aug/20

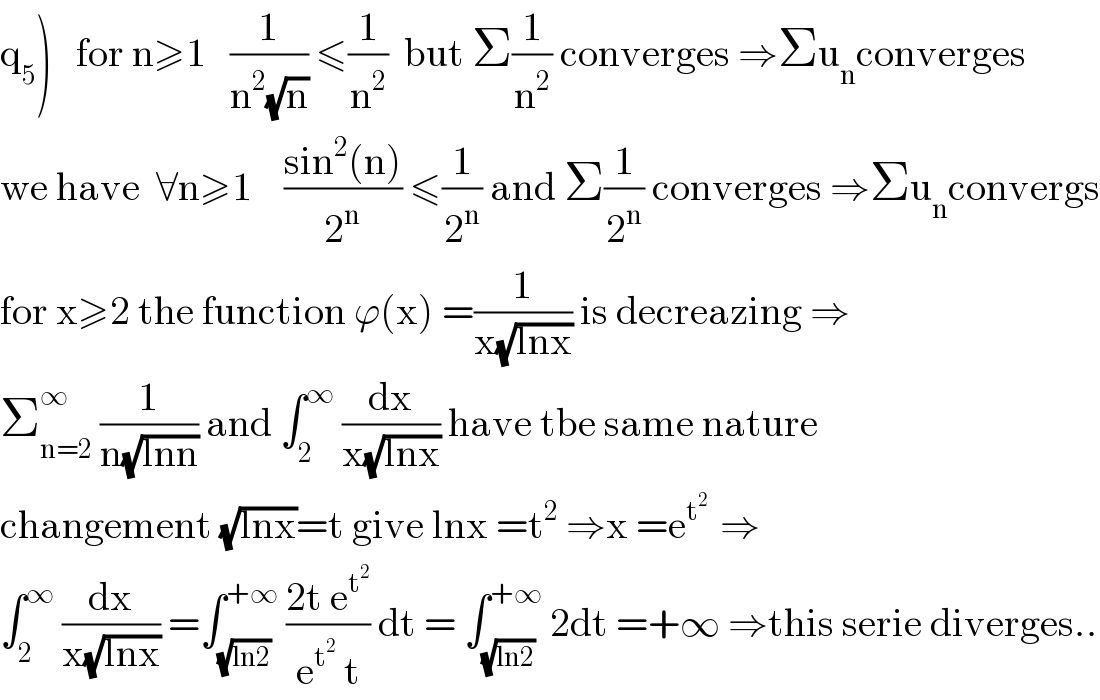
q_5 ) for n≥1 (1/(n^2 (√n))) ≤(1/n^2 ) but Σ(1/n^2 ) converges ⇒Σu_n converges we have ∀n≥1 ((sin^2 (n))/2^n ) ≤(1/2^n ) and Σ(1/2^n ) converges ⇒Σu_n convergs for x≥2 the function ϕ(x) =(1/(x(√(lnx)))) is decreazing ⇒ Σ_(n=2) ^∞ (1/(n(√(lnn)))) and ∫_2 ^∞ (dx/(x(√(lnx)))) have tbe same nature changement (√(lnx))=t give lnx =t^2 ⇒x =e^(t^2 ) ⇒ ∫_2 ^∞ (dx/(x(√(lnx)))) =∫_(√(ln2)) ^(+∞) ((2t e^t^2 )/(e^t^2 t)) dt = ∫_(√(ln2)) ^(+∞) 2dt =+∞ ⇒this serie diverges..

$$\left.\mathrm{q}_{\mathrm{5}} \right)\:\:\:\mathrm{for}\:\mathrm{n}\geqslant\mathrm{1}\:\:\:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} \sqrt{\mathrm{n}}}\:\leqslant\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\:\:\mathrm{but}\:\Sigma\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\:\mathrm{converges}\:\Rightarrow\Sigma\mathrm{u}_{\mathrm{n}} \mathrm{converges} \\ $$$$\mathrm{we}\:\mathrm{have}\:\:\forall\mathrm{n}\geqslant\mathrm{1}\:\:\:\:\frac{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{n}\right)}{\mathrm{2}^{\mathrm{n}} }\:\leqslant\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\:\mathrm{and}\:\Sigma\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\:\mathrm{converges}\:\Rightarrow\Sigma\mathrm{u}_{\mathrm{n}} \mathrm{convergs} \\ $$$$\mathrm{for}\:\mathrm{x}\geqslant\mathrm{2}\:\mathrm{the}\:\mathrm{function}\:\varphi\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{x}\sqrt{\mathrm{lnx}}}\:\mathrm{is}\:\mathrm{decreazing}\:\Rightarrow \\ $$$$\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}\sqrt{\mathrm{lnn}}}\:\mathrm{and}\:\int_{\mathrm{2}} ^{\infty} \:\frac{\mathrm{dx}}{\mathrm{x}\sqrt{\mathrm{lnx}}}\:\mathrm{have}\:\mathrm{tbe}\:\mathrm{same}\:\mathrm{nature} \\ $$$$\mathrm{changement}\:\sqrt{\mathrm{lnx}}=\mathrm{t}\:\mathrm{give}\:\mathrm{lnx}\:=\mathrm{t}^{\mathrm{2}} \:\Rightarrow\mathrm{x}\:=\mathrm{e}^{\mathrm{t}^{\mathrm{2}} \:} \:\Rightarrow \\ $$$$\int_{\mathrm{2}} ^{\infty} \:\frac{\mathrm{dx}}{\mathrm{x}\sqrt{\mathrm{lnx}}}\:=\int_{\sqrt{\mathrm{ln2}}} ^{+\infty} \:\frac{\mathrm{2t}\:\mathrm{e}^{\mathrm{t}^{\mathrm{2}} } }{\mathrm{e}^{\mathrm{t}^{\mathrm{2}} } \:\mathrm{t}}\:\mathrm{dt}\:=\:\int_{\sqrt{\mathrm{ln2}}} ^{+\infty} \:\mathrm{2dt}\:=+\infty\:\Rightarrow\mathrm{this}\:\mathrm{serie}\:\mathrm{diverges}.. \\ $$

Commented by mohammad17 last updated on 02/Aug/20

$${thank}\:{you}\:{sir} \\ $$

Commented by abdomathmax last updated on 02/Aug/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir} \\ $$

Answered by mathmax by abdo last updated on 02/Aug/20

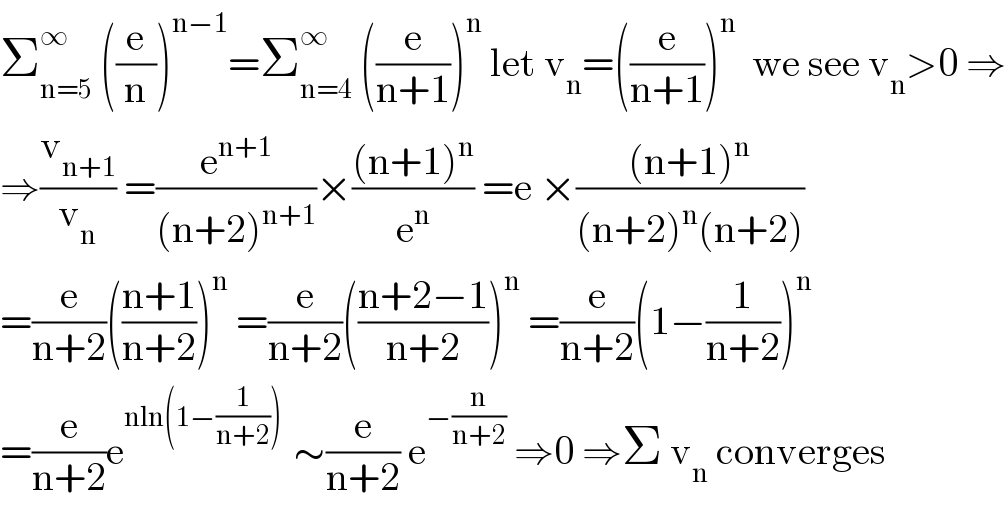
Σ_(n=5) ^∞ ((e/n))^(n−1) =Σ_(n=4) ^∞ ((e/(n+1)))^n let v_n =((e/(n+1)))^n we see v_n >0 ⇒ ⇒(v_(n+1) /v_n ) =(e^(n+1) /((n+2)^(n+1) ))×(((n+1)^n )/e^n ) =e ×(((n+1)^n )/((n+2)^n (n+2))) =(e/(n+2))(((n+1)/(n+2)))^n =(e/(n+2))(((n+2−1)/(n+2)))^n =(e/(n+2))(1−(1/(n+2)))^n =(e/(n+2))e^(nln(1−(1/(n+2))) ) ∼(e/(n+2)) e^(−(n/(n+2))) ⇒0 ⇒Σ v_n converges

$$\sum_{\mathrm{n}=\mathrm{5}} ^{\infty} \:\left(\frac{\mathrm{e}}{\mathrm{n}}\right)^{\mathrm{n}−\mathrm{1}} =\sum_{\mathrm{n}=\mathrm{4}} ^{\infty} \:\left(\frac{\mathrm{e}}{\mathrm{n}+\mathrm{1}}\right)^{\mathrm{n}} \:\mathrm{let}\:\mathrm{v}_{\mathrm{n}} =\left(\frac{\mathrm{e}}{\mathrm{n}+\mathrm{1}}\right)^{\mathrm{n}} \:\:\mathrm{we}\:\mathrm{see}\:\mathrm{v}_{\mathrm{n}} >\mathrm{0}\:\Rightarrow \\ $$$$\Rightarrow\frac{\mathrm{v}_{\mathrm{n}+\mathrm{1}} }{\mathrm{v}_{\mathrm{n}} }\:=\frac{\mathrm{e}^{\mathrm{n}+\mathrm{1}} }{\left(\mathrm{n}+\mathrm{2}\right)^{\mathrm{n}+\mathrm{1}} }×\frac{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{e}^{\mathrm{n}} }\:=\mathrm{e}\:×\frac{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{n}+\mathrm{2}\right)^{\mathrm{n}} \left(\mathrm{n}+\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{e}}{\mathrm{n}+\mathrm{2}}\left(\frac{\mathrm{n}+\mathrm{1}}{\mathrm{n}+\mathrm{2}}\right)^{\mathrm{n}} \:=\frac{\mathrm{e}}{\mathrm{n}+\mathrm{2}}\left(\frac{\mathrm{n}+\mathrm{2}−\mathrm{1}}{\mathrm{n}+\mathrm{2}}\right)^{\mathrm{n}} \:=\frac{\mathrm{e}}{\mathrm{n}+\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}\right)^{\mathrm{n}} \\ $$$$=\frac{\mathrm{e}}{\mathrm{n}+\mathrm{2}}\mathrm{e}^{\mathrm{nln}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}\right)\:} \:\sim\frac{\mathrm{e}}{\mathrm{n}+\mathrm{2}}\:\mathrm{e}^{−\frac{\mathrm{n}}{\mathrm{n}+\mathrm{2}}} \:\Rightarrow\mathrm{0}\:\Rightarrow\Sigma\:\mathrm{v}_{\mathrm{n}} \:\mathrm{converges} \\ $$

Commented by mohammad17 last updated on 02/Aug/20

$${thank}\:{you}\:{sir} \\ $$

Commented by abdomathmax last updated on 02/Aug/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply