Question-106094

Question Number 106094 by Dwaipayan Shikari last updated on 02/Aug/20

Commented by Dwaipayan Shikari last updated on 02/Aug/20

Dwaipayan Shikari: The wedge's Surface is friction less (where the ball of mass 'm' will roll) and the friction coefficient between wedge and the ground is also negligible.( An oily surface ��) Calculate the velocity of the wedge when the ball will fly off. Additional information is on the picture

Commented by Dwaipayan Shikari last updated on 02/Aug/20

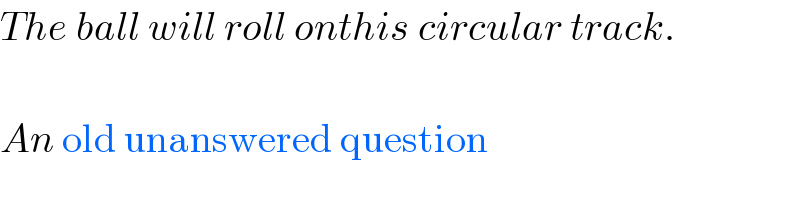
The ball will roll onthis circular track. An old unanswered question

$${The}\:{ball}\:{will}\:{roll}\:{onthis}\:{circular}\:{track}. \\ $$$$ \\ $$$${An}\:\mathrm{old}\:\mathrm{unanswered}\:\mathrm{question} \\ $$

Commented by mr W last updated on 02/Aug/20

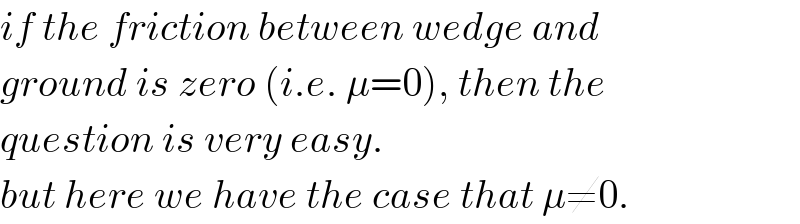
if the friction between wedge and ground is zero (i.e. μ=0), then the question is very easy. but here we have the case that μ≠0.

$${if}\:{the}\:{friction}\:{between}\:{wedge}\:{and}\: \\ $$$${ground}\:{is}\:{zero}\:\left({i}.{e}.\:\mu=\mathrm{0}\right),\:{then}\:{the}\: \\ $$$${question}\:{is}\:{very}\:{easy}. \\ $$$${but}\:{here}\:{we}\:{have}\:{the}\:{case}\:{that}\:\mu\neq\mathrm{0}. \\ $$

Commented by mr W last updated on 02/Aug/20

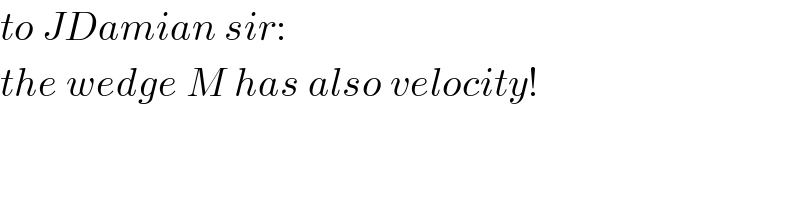
$${to}\:{JDamian}\:{sir}: \\ $$$${the}\:{wedge}\:{M}\:{has}\:{also}\:{velocity}! \\ $$

Commented by Dwaipayan Shikari last updated on 02/Aug/20

U+KE=u+ke mgR+0=0+(1/2)mv^2 +(1/2)MV^2 2mgR=mv^2 +MV^2 →(a) Momentum of the system is conserved (M+m).0=MV+mv V=−((mv)/M) 2mgR=mv^2 +M.((m^2 v^2 )/M^2 ) 2gR=v^2 (1+(m/M)) v=(√((2gR)/((1+(m/M))))) V=−((mv)/M)=−(m/M)(√((2gR)/((1+(m/M))))) Frictional case: mgR=(1/2)MV^2 +(1/2)mv^2 +W_((by the frictional force))

$$\mathrm{U}+\mathrm{KE}={u}+{ke} \\ $$$${mgR}+\mathrm{0}=\mathrm{0}+\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{MV}^{\mathrm{2}} \\ $$$$\mathrm{2}{mgR}={mv}^{\mathrm{2}} +{MV}^{\mathrm{2}} \rightarrow\left({a}\right) \\ $$$$ \\ $$$${Momentum}\:{of}\:{the}\:{system}\:{is}\:{conserved} \\ $$$$\left({M}+{m}\right).\mathrm{0}={MV}+{mv} \\ $$$${V}=−\frac{{mv}}{{M}} \\ $$$$\mathrm{2}{mgR}={mv}^{\mathrm{2}} +{M}.\frac{{m}^{\mathrm{2}} {v}^{\mathrm{2}} }{{M}^{\mathrm{2}} } \\ $$$$\mathrm{2}{gR}={v}^{\mathrm{2}} \left(\mathrm{1}+\frac{{m}}{{M}}\right) \\ $$$${v}=\sqrt{\frac{\mathrm{2}{gR}}{\left(\mathrm{1}+\frac{{m}}{{M}}\right)}} \\ $$$${V}=−\frac{{mv}}{{M}}=−\frac{{m}}{{M}}\sqrt{\frac{\mathrm{2}{gR}}{\left(\mathrm{1}+\frac{{m}}{{M}}\right)}} \\ $$$$\mathrm{Frictional}\:\mathrm{case}: \\ $$$$\mathrm{mgR}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{MV}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{mv}^{\mathrm{2}} +\mathrm{W}_{\left(\mathrm{by}\:\mathrm{the}\:\mathrm{frictional}\:\mathrm{force}\right)} \\ $$$$ \\ $$$$ \\ $$

Commented by Dwaipayan Shikari last updated on 02/Aug/20

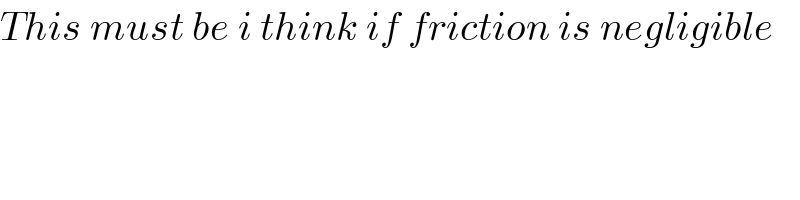
$${This}\:{must}\:{be}\:{i}\:{think}\:{if}\:{friction}\:{is}\:{negligible} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply