Question-106302

Question Number 106302 by mathdave last updated on 04/Aug/20

Answered by bemath last updated on 04/Aug/20

x = sin ♭ ⇒ ∫ ((cos ♭ d♭)/(sin^2 ♭ cos ♭)) = ∫ csc^2 ♭ d♭ = −∫ d(cot ♭) = −cot ♭ + C = −((√(1−x^2 ))/x) + C

$$\mathrm{x}\:=\:\mathrm{sin}\:\flat\:\Rightarrow\:\int\:\frac{\mathrm{cos}\:\flat\:\mathrm{d}\flat}{\mathrm{sin}\:^{\mathrm{2}} \flat\:\mathrm{cos}\:\flat}\:= \\ $$$$\int\:\mathrm{csc}^{\mathrm{2}} \:\flat\:\mathrm{d}\flat\:=\:−\int\:\mathrm{d}\left(\mathrm{cot}\:\flat\right)\: \\ $$$$=\:−\mathrm{cot}\:\flat\:+\:\mathrm{C}\:=\:−\frac{\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}{\mathrm{x}}\:+\:\mathrm{C}\: \\ $$

Answered by 1549442205PVT last updated on 04/Aug/20

Set x=sinϕ⇒dx=cosϕdϕ(ϕ∈[((−π)/2);(π/2)]) F=∫((cosϕdϕ)/(sin^2 ϕcosϕ))=∫(dϕ/(sin^2 ϕ))=−cotϕ+C =((−cos𝛟)/(sin𝛟))+C=((−(√(1−x^2 )))/x)+C

$$\mathrm{Set}\:\mathrm{x}=\mathrm{sin}\varphi\Rightarrow\mathrm{dx}=\mathrm{cos}\varphi\mathrm{d}\varphi\left(\varphi\in\left[\frac{−\pi}{\mathrm{2}};\frac{\pi}{\mathrm{2}}\right]\right) \\ $$$$\mathrm{F}=\int\frac{\mathrm{cos}\varphi\mathrm{d}\varphi}{\mathrm{sin}^{\mathrm{2}} \varphi\mathrm{cos}\varphi}=\int\frac{\mathrm{d}\varphi}{\mathrm{sin}^{\mathrm{2}} \varphi}=−\mathrm{cot}\varphi+\mathrm{C} \\ $$$$=\frac{−\boldsymbol{\mathrm{cos}\varphi}}{\boldsymbol{\mathrm{sin}\varphi}}+\boldsymbol{\mathrm{C}}=\frac{−\sqrt{\mathrm{1}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} }}{\boldsymbol{\mathrm{x}}}+\boldsymbol{\mathrm{C}} \\ $$

Answered by Ar Brandon last updated on 04/Aug/20

t=(1/x) ⇒ dt=−(1/x^2 )dx ⇒I=−∫(dt/( (√(1−(1/t^2 )))))=−∫(t/( (√(t^2 −1))))dt ⇒I=−(1/2)∙(2/1)(√(t^2 −1))=−(√((1/x^2 )−1))=−(√((1−x^2 )/x^2 ))+C

$$\mathrm{t}=\frac{\mathrm{1}}{\mathrm{x}}\:\Rightarrow\:\mathrm{dt}=−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$\Rightarrow\mathcal{I}=−\int\frac{\mathrm{dt}}{\:\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}}=−\int\frac{\mathrm{t}}{\:\sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}}\mathrm{dt} \\ $$$$\Rightarrow\mathcal{I}=−\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\mathrm{2}}{\mathrm{1}}\sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}=−\sqrt{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\mathrm{1}}=−\sqrt{\frac{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }}+\mathcal{C} \\ $$

Answered by mathmax by abdo last updated on 05/Aug/20

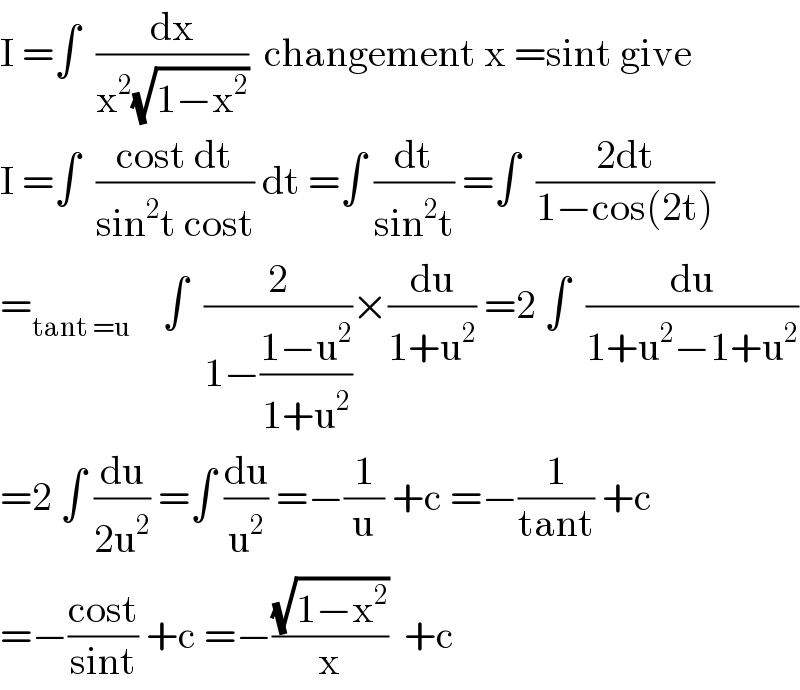
I =∫ (dx/(x^2 (√(1−x^2 )))) changement x =sint give I =∫ ((cost dt)/(sin^2 t cost)) dt =∫ (dt/(sin^2 t)) =∫ ((2dt)/(1−cos(2t))) =_(tant =u) ∫ (2/(1−((1−u^2 )/(1+u^2 ))))×(du/(1+u^2 )) =2 ∫ (du/(1+u^2 −1+u^2 )) =2 ∫ (du/(2u^2 )) =∫ (du/u^2 ) =−(1/u) +c =−(1/(tant)) +c =−((cost)/(sint)) +c =−((√(1−x^2 ))/x) +c

$$\mathrm{I}\:=\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\:\:\mathrm{changement}\:\mathrm{x}\:=\mathrm{sint}\:\mathrm{give}\: \\ $$$$\mathrm{I}\:=\int\:\:\frac{\mathrm{cost}\:\mathrm{dt}}{\mathrm{sin}^{\mathrm{2}} \mathrm{t}\:\mathrm{cost}}\:\mathrm{dt}\:=\int\:\frac{\mathrm{dt}}{\mathrm{sin}^{\mathrm{2}} \mathrm{t}}\:=\int\:\:\frac{\mathrm{2dt}}{\mathrm{1}−\mathrm{cos}\left(\mathrm{2t}\right)} \\ $$$$=_{\mathrm{tant}\:=\mathrm{u}} \:\:\:\:\int\:\:\frac{\mathrm{2}}{\mathrm{1}−\frac{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }}×\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\:=\mathrm{2}\:\int\:\:\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} −\mathrm{1}+\mathrm{u}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\:\int\:\frac{\mathrm{du}}{\mathrm{2u}^{\mathrm{2}} }\:=\int\:\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} }\:=−\frac{\mathrm{1}}{\mathrm{u}}\:+\mathrm{c}\:=−\frac{\mathrm{1}}{\mathrm{tant}}\:+\mathrm{c} \\ $$$$=−\frac{\mathrm{cost}}{\mathrm{sint}}\:+\mathrm{c}\:=−\frac{\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}{\mathrm{x}}\:\:+\mathrm{c} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply