Menu Close

Question-106319

Tinku Tara 0 Comments
Pin




Question Number 106319 by mohammad17 last updated on 04/Aug/20
Commented by mohammad17 last updated on 04/Aug/20
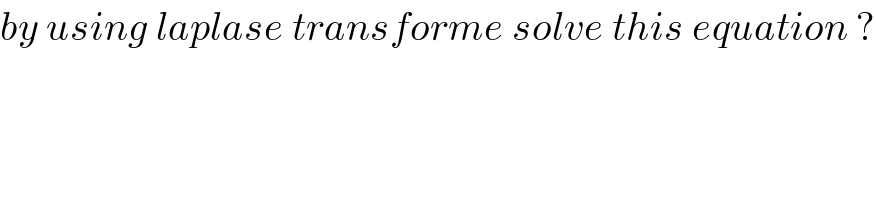
by using laplase transforme solve this equation ?
$${by}\:{using}\:{laplase}\:{transforme}\:{solve}\:{this}\:{equation}\:? \\ $$
Commented by rexfordattacudjoe last updated on 04/Aug/20
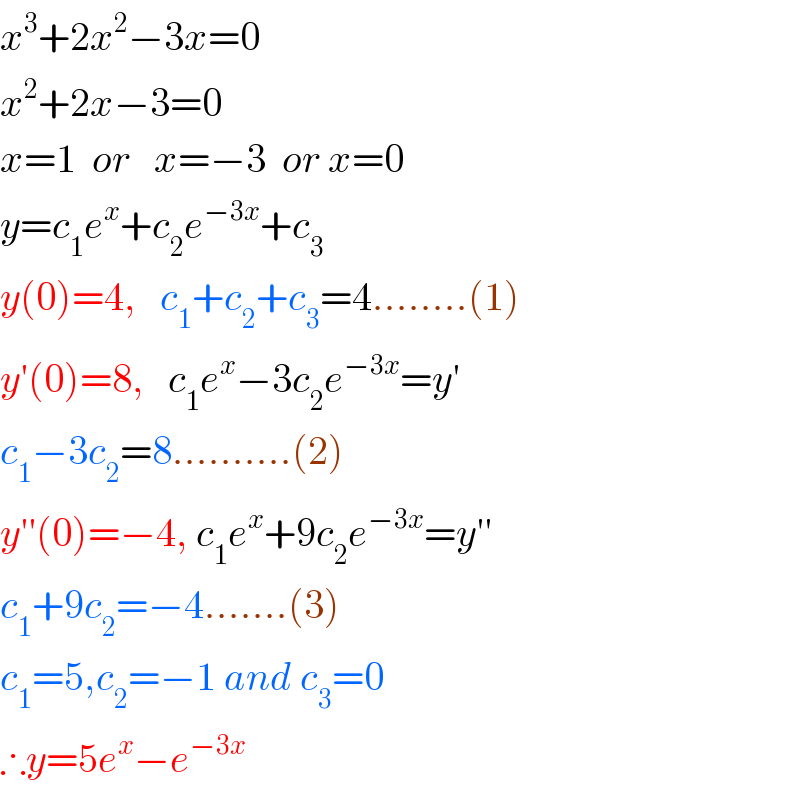
x^3 +2x^2 −3x=0 x^2 +2x−3=0 x=1 or x=−3 or x=0 y=c_1 e^x +c_2 e^(−3x) +c_3 y(0)=4, c_1 +c_2 +c_3 =4........(1) y′(0)=8, c_1 e^x −3c_2 e^(−3x) =y′ c_1 −3c_2 =8..........(2) y′′(0)=−4, c_1 e^x +9c_2 e^(−3x) =y′′ c_1 +9c_2 =−4.......(3) c_1 =5,c_2 =−1 and c_3 =0 ∴y=5e^x −e^(−3x)
$${x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}=\mathrm{0} \\ $$$${x}=\mathrm{1}\:\:{or}\:\:\:{x}=−\mathrm{3}\:\:{or}\:{x}=\mathrm{0} \\ $$$${y}={c}_{\mathrm{1}} {e}^{{x}} +{c}_{\mathrm{2}} {e}^{−\mathrm{3}{x}} +{c}_{\mathrm{3}} \\ $$$${y}\left(\mathrm{0}\right)=\mathrm{4},\:\:\:{c}_{\mathrm{1}} +{c}_{\mathrm{2}} +{c}_{\mathrm{3}} =\mathrm{4}……..\left(\mathrm{1}\right) \\ $$$${y}'\left(\mathrm{0}\right)=\mathrm{8},\:\:\:{c}_{\mathrm{1}} {e}^{{x}} −\mathrm{3}{c}_{\mathrm{2}} {e}^{−\mathrm{3}{x}} ={y}' \\ $$$${c}_{\mathrm{1}} −\mathrm{3}{c}_{\mathrm{2}} =\mathrm{8}……….\left(\mathrm{2}\right) \\ $$$${y}''\left(\mathrm{0}\right)=−\mathrm{4},\:{c}_{\mathrm{1}} {e}^{{x}} +\mathrm{9}{c}_{\mathrm{2}} {e}^{−\mathrm{3}{x}} ={y}'' \\ $$$${c}_{\mathrm{1}} +\mathrm{9}{c}_{\mathrm{2}} =−\mathrm{4}…….\left(\mathrm{3}\right) \\ $$$${c}_{\mathrm{1}} =\mathrm{5},{c}_{\mathrm{2}} =−\mathrm{1}\:{and}\:{c}_{\mathrm{3}} =\mathrm{0} \\ $$$$\therefore{y}=\mathrm{5}{e}^{{x}} −{e}^{−\mathrm{3}{x}} \\ $$
Answered by mathmax by abdo last updated on 04/Aug/20
y^((3)) +2y^((2)) −3y^((1)) =0 ⇒ L(y^((3)) )+2L(y^((2)) )−3L(y^((1)) ) =0 ⇒ x^3 L(y)−x^2 y(0)−xy^′ (0)−y^(′′) (0) +2(x^2 L(y)−xy(o)−y^′ (0)) −3(xL(y)−y(0) =0 ⇒ x^3 L(y)−4x^2 −8x +4 +2(x^2 L(y)−4x−8)−3(xL(y)−4) =0 ⇒ (x^3 +2x^2 −3x)L(y) −4x^2 −8x +4−8x−16 +12 =0 ⇒ (x^3 +2x^2 −3x)L(y) −4x^2 −16x =0 ⇒ (x^2 +2x−3)L(y)−4x−16 =0 ⇒L(y) =((4x+16)/(x^2 +2x−3)) ⇒ y(x) =L^(−1) (((4x+16)/(x^2 +2x−3))) let decompose f(x) =((4x+16)/(x^2 +2x−3)) x^2 +2x−3 =0→Δ^′ =1+3 =4 ⇒x_1 =−1+2 =1 x_2 =−1−2 =−3 ⇒f(x) =((4x+16)/((x−1)(x+3))) =(a/(x−1)) +(b/(x+3)) a =((20)/4) =5 and b =(4/(−4)) =−1 ⇒f(x) =(5/(x−1))−(1/(x+3)) ⇒ L^(−1) (f) =5e^x −e^(−3x) ⇒ y(x) =5e^x −e^(−3x)
$$\mathrm{y}^{\left(\mathrm{3}\right)} \:+\mathrm{2y}^{\left(\mathrm{2}\right)} −\mathrm{3y}^{\left(\mathrm{1}\right)} \:=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{L}\left(\mathrm{y}^{\left(\mathrm{3}\right)} \right)+\mathrm{2L}\left(\mathrm{y}^{\left(\mathrm{2}\right)} \right)−\mathrm{3L}\left(\mathrm{y}^{\left(\mathrm{1}\right)} \right)\:=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{x}^{\mathrm{3}} \mathrm{L}\left(\mathrm{y}\right)−\mathrm{x}^{\mathrm{2}} \mathrm{y}\left(\mathrm{0}\right)−\mathrm{xy}^{'} \left(\mathrm{0}\right)−\mathrm{y}^{''} \left(\mathrm{0}\right)\:+\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} \mathrm{L}\left(\mathrm{y}\right)−\mathrm{xy}\left(\mathrm{o}\right)−\mathrm{y}^{'} \left(\mathrm{0}\right)\right) \\ $$$$−\mathrm{3}\left(\mathrm{xL}\left(\mathrm{y}\right)−\mathrm{y}\left(\mathrm{0}\right)\:=\mathrm{0}\:\Rightarrow\right. \\ $$$$\mathrm{x}^{\mathrm{3}} \:\mathrm{L}\left(\mathrm{y}\right)−\mathrm{4x}^{\mathrm{2}} −\mathrm{8x}\:+\mathrm{4}\:\:+\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} \:\mathrm{L}\left(\mathrm{y}\right)−\mathrm{4x}−\mathrm{8}\right)−\mathrm{3}\left(\mathrm{xL}\left(\mathrm{y}\right)−\mathrm{4}\right)\:=\mathrm{0}\:\Rightarrow \\ $$$$\left(\mathrm{x}^{\mathrm{3}} \:+\mathrm{2x}^{\mathrm{2}} −\mathrm{3x}\right)\mathrm{L}\left(\mathrm{y}\right)\:−\mathrm{4x}^{\mathrm{2}} −\mathrm{8x}\:+\mathrm{4}−\mathrm{8x}−\mathrm{16}\:+\mathrm{12}\:=\mathrm{0}\:\Rightarrow \\ $$$$\left(\mathrm{x}^{\mathrm{3}} \:+\mathrm{2x}^{\mathrm{2}} −\mathrm{3x}\right)\mathrm{L}\left(\mathrm{y}\right)\:−\mathrm{4x}^{\mathrm{2}} −\mathrm{16x}\:\:=\mathrm{0}\:\Rightarrow \\ $$$$\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}−\mathrm{3}\right)\mathrm{L}\left(\mathrm{y}\right)−\mathrm{4x}−\mathrm{16}\:=\mathrm{0}\:\Rightarrow\mathrm{L}\left(\mathrm{y}\right)\:=\frac{\mathrm{4x}+\mathrm{16}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}−\mathrm{3}}\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{4x}+\mathrm{16}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}−\mathrm{3}}\right)\:\mathrm{let}\:\:\mathrm{decompose}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{4x}+\mathrm{16}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}−\mathrm{3}} \\ $$$$\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}−\mathrm{3}\:=\mathrm{0}\rightarrow\Delta^{'} \:=\mathrm{1}+\mathrm{3}\:=\mathrm{4}\:\Rightarrow\mathrm{x}_{\mathrm{1}} =−\mathrm{1}+\mathrm{2}\:=\mathrm{1} \\ $$$$\mathrm{x}_{\mathrm{2}} =−\mathrm{1}−\mathrm{2}\:=−\mathrm{3}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{4x}+\mathrm{16}}{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{3}\right)}\:=\frac{\mathrm{a}}{\mathrm{x}−\mathrm{1}}\:+\frac{\mathrm{b}}{\mathrm{x}+\mathrm{3}} \\ $$$$\mathrm{a}\:=\frac{\mathrm{20}}{\mathrm{4}}\:=\mathrm{5}\:\:\mathrm{and}\:\mathrm{b}\:=\frac{\mathrm{4}}{−\mathrm{4}}\:=−\mathrm{1}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{5}}{\mathrm{x}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{3}}\:\Rightarrow \\ $$$$\mathrm{L}^{−\mathrm{1}} \left(\mathrm{f}\right)\:=\mathrm{5e}^{\mathrm{x}} \:−\mathrm{e}^{−\mathrm{3x}} \:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{5e}^{\mathrm{x}} −\mathrm{e}^{−\mathrm{3x}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *