Question-106366

Question Number 106366 by 175mohamed last updated on 04/Aug/20

Answered by mathmax by abdo last updated on 05/Aug/20

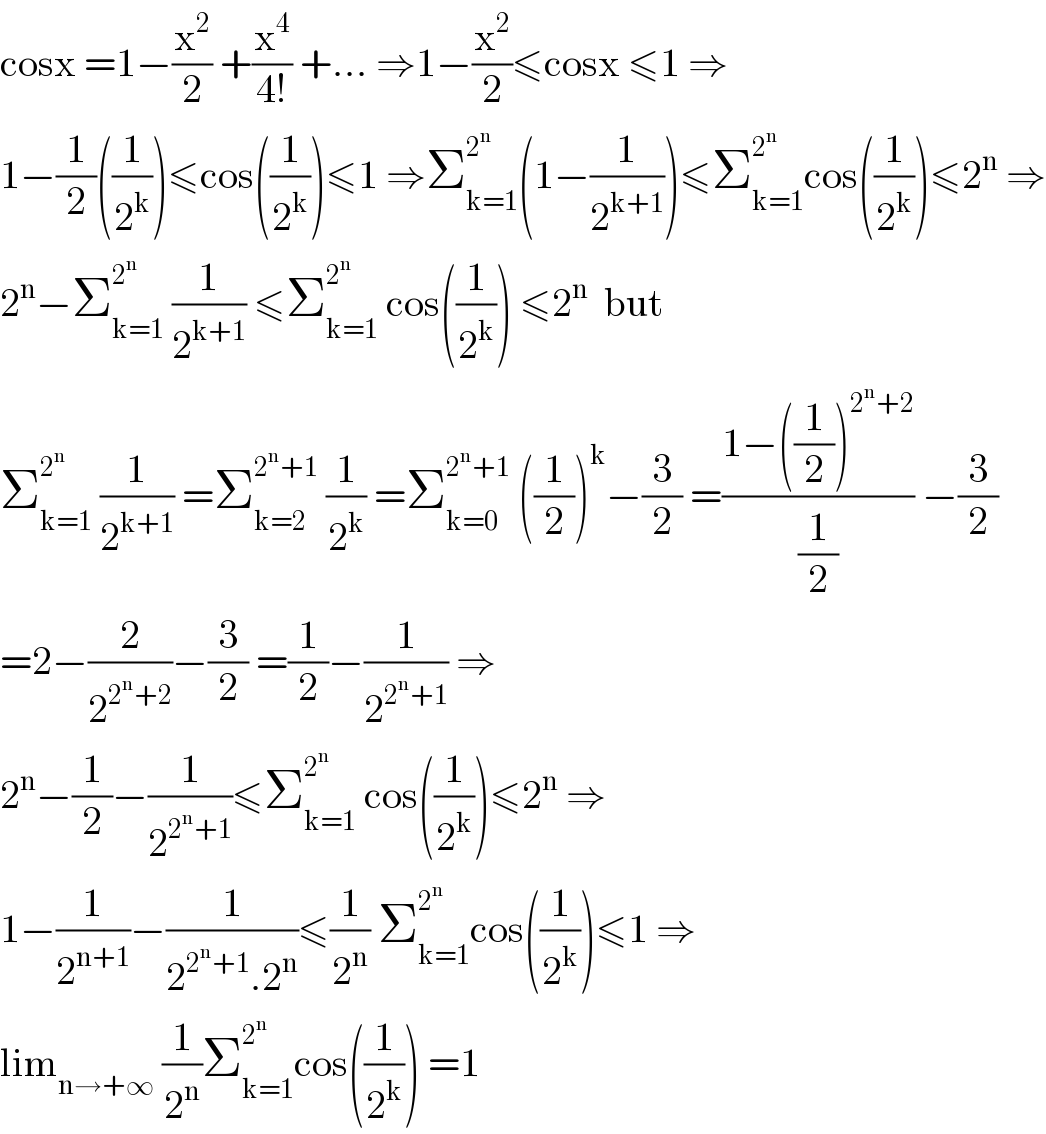
cosx =1−(x^2 /2) +(x^4 /(4!)) +... ⇒1−(x^2 /2)≤cosx ≤1 ⇒ 1−(1/2)((1/2^k ))≤cos((1/2^k ))≤1 ⇒Σ_(k=1) ^2^n (1−(1/2^(k+1) ))≤Σ_(k=1) ^2^n cos((1/2^k ))≤2^n ⇒ 2^n −Σ_(k=1) ^2^n (1/2^(k+1) ) ≤Σ_(k=1) ^2^n cos((1/2^k )) ≤2^n but Σ_(k=1) ^2^n (1/2^(k+1) ) =Σ_(k=2) ^(2^n +1) (1/2^k ) =Σ_(k=0) ^(2^n +1) ((1/2))^k −(3/2) =((1−((1/2))^(2^n +2) )/(1/2)) −(3/2) =2−(2/2^(2^n +2) )−(3/2) =(1/2)−(1/2^(2^n +1) ) ⇒ 2^n −(1/2)−(1/2^(2^n +1) )≤Σ_(k=1) ^2^n cos((1/2^k ))≤2^n ⇒ 1−(1/2^(n+1) )−(1/(2^(2^n +1) .2^n ))≤(1/2^n ) Σ_(k=1) ^2^n cos((1/2^k ))≤1 ⇒ lim_(n→+∞) (1/2^n )Σ_(k=1) ^2^n cos((1/2^k )) =1

$$\mathrm{cosx}\:=\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{4}!}\:+…\:\Rightarrow\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\leqslant\mathrm{cosx}\:\leqslant\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}} }\right)\leqslant\mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}} }\right)\leqslant\mathrm{1}\:\Rightarrow\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{2}^{\mathrm{n}} } \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}+\mathrm{1}} }\right)\leqslant\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{2}^{\mathrm{n}} } \mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}} }\right)\leqslant\mathrm{2}^{\mathrm{n}} \:\Rightarrow \\ $$$$\mathrm{2}^{\mathrm{n}} −\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{2}^{\mathrm{n}} } \:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}+\mathrm{1}} }\:\leqslant\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{2}^{\mathrm{n}} } \:\mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}} }\right)\:\leqslant\mathrm{2}^{\mathrm{n}} \:\:\mathrm{but} \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{2}^{\mathrm{n}} } \:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}+\mathrm{1}} }\:=\sum_{\mathrm{k}=\mathrm{2}} ^{\mathrm{2}^{\mathrm{n}} +\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}} }\:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2}^{\mathrm{n}} +\mathrm{1}} \:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{k}} −\frac{\mathrm{3}}{\mathrm{2}}\:=\frac{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}^{\mathrm{n}} +\mathrm{2}} }{\frac{\mathrm{1}}{\mathrm{2}}}\:−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$=\mathrm{2}−\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{2}^{\mathrm{n}} +\mathrm{2}} }−\frac{\mathrm{3}}{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}^{\mathrm{n}} +\mathrm{1}} }\:\Rightarrow \\ $$$$\mathrm{2}^{\mathrm{n}} −\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}^{\mathrm{n}} +\mathrm{1}} }\leqslant\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{2}^{\mathrm{n}} } \:\mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}} }\right)\leqslant\mathrm{2}^{\mathrm{n}} \:\Rightarrow \\ $$$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}+\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}^{\mathrm{n}} +\mathrm{1}} .\mathrm{2}^{\mathrm{n}} }\leqslant\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{2}^{\mathrm{n}} } \mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}} }\right)\leqslant\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{2}^{\mathrm{n}} } \mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}} }\right)\:=\mathrm{1} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply