Question Number 106378 by mr W last updated on 04/Aug/20

Answered by Dwaipayan Shikari last updated on 05/Aug/20

$$\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{6}}\right)….{n} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}}\right)={y} \\ $$$${log}\left(\underset{{n}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}}\right)\right)={logy} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}{log}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}}\right)={log}\:{y} \\ $$$$\frac{\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}{log}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}}\right)}{{n}}\geqslant\left(\underset{{n}=\mathrm{1}} {\overset{{n}} {\prod}}{log}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}}\right)\right)^{\frac{\mathrm{1}}{{n}}} \\ $$$$\frac{{log}\left(\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{3}}{\mathrm{4}}……\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}{n}}\right)}{{n}}\geqslant\left(\overset{{n}} {\prod}{log}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}}\right)\right)^{\frac{\mathrm{1}}{{n}}} \\ $$
Commented by mr W last updated on 05/Aug/20
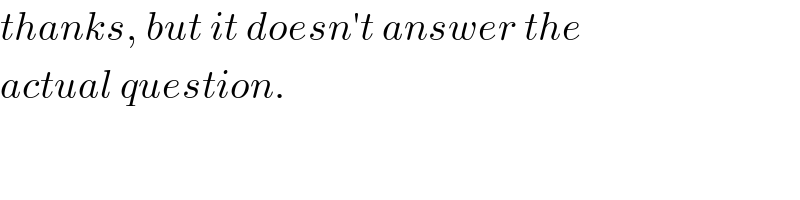
$${thanks},\:{but}\:{it}\:{doesn}'{t}\:{answer}\:{the} \\ $$$${actual}\:{question}. \\ $$
Answered by mr W last updated on 05/Aug/20

