Menu Close

Question-106379

Tinku Tara 0 Comments
Pin




Question Number 106379 by Algoritm last updated on 04/Aug/20
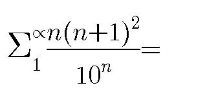
Answered by mr W last updated on 04/Aug/20
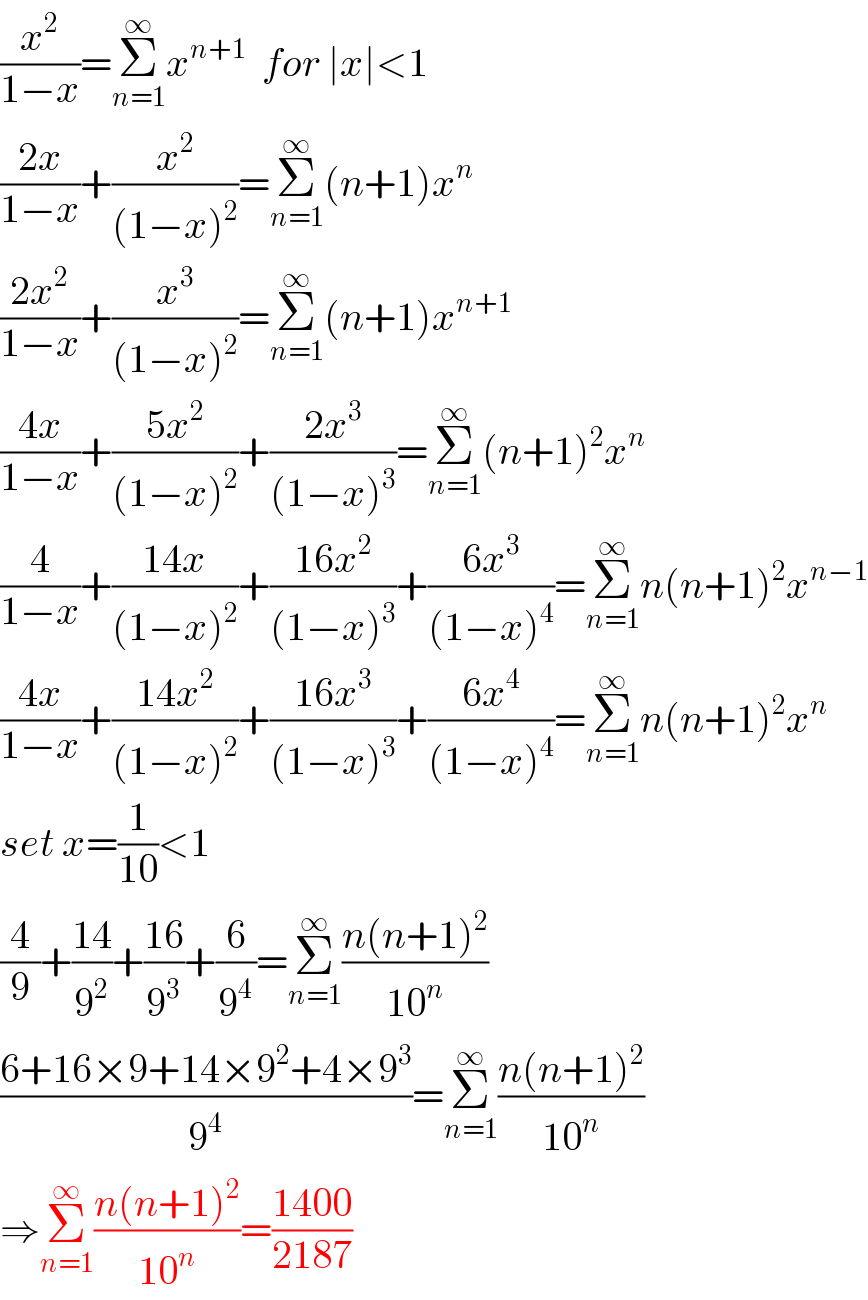
(x^2 /(1−x))=Σ_(n=1) ^∞ x^(n+1) for ∣x∣<1 ((2x)/(1−x))+(x^2 /((1−x)^2 ))=Σ_(n=1) ^∞ (n+1)x^n ((2x^2 )/(1−x))+(x^3 /((1−x)^2 ))=Σ_(n=1) ^∞ (n+1)x^(n+1) ((4x)/(1−x))+((5x^2 )/((1−x)^2 ))+((2x^3 )/((1−x)^3 ))=Σ_(n=1) ^∞ (n+1)^2 x^n (4/(1−x))+((14x)/((1−x)^2 ))+((16x^2 )/((1−x)^3 ))+((6x^3 )/((1−x)^4 ))=Σ_(n=1) ^∞ n(n+1)^2 x^(n−1) ((4x)/(1−x))+((14x^2 )/((1−x)^2 ))+((16x^3 )/((1−x)^3 ))+((6x^4 )/((1−x)^4 ))=Σ_(n=1) ^∞ n(n+1)^2 x^n set x=(1/(10))<1 (4/9)+((14)/9^2 )+((16)/9^3 )+(6/9^4 )=Σ_(n=1) ^∞ ((n(n+1)^2 )/(10^n )) ((6+16×9+14×9^2 +4×9^3 )/9^4 )=Σ_(n=1) ^∞ ((n(n+1)^2 )/(10^n )) ⇒Σ_(n=1) ^∞ ((n(n+1)^2 )/(10^n ))=((1400)/(2187))
$$\frac{{x}^{\mathrm{2}} }{\mathrm{1}−{x}}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{x}^{{n}+\mathrm{1}} \:\:{for}\:\mid{x}\mid<\mathrm{1} \\ $$$$\frac{\mathrm{2}{x}}{\mathrm{1}−{x}}+\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left({n}+\mathrm{1}\right){x}^{{n}} \\ $$$$\frac{\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{1}−{x}}+\frac{{x}^{\mathrm{3}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left({n}+\mathrm{1}\right){x}^{{n}+\mathrm{1}} \\ $$$$\frac{\mathrm{4}{x}}{\mathrm{1}−{x}}+\frac{\mathrm{5}{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{\mathrm{2}{x}^{\mathrm{3}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left({n}+\mathrm{1}\right)^{\mathrm{2}} {x}^{{n}} \\ $$$$\frac{\mathrm{4}}{\mathrm{1}−{x}}+\frac{\mathrm{14}{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{\mathrm{16}{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }+\frac{\mathrm{6}{x}^{\mathrm{3}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} }=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{n}\left({n}+\mathrm{1}\right)^{\mathrm{2}} {x}^{{n}−\mathrm{1}} \\ $$$$\frac{\mathrm{4}{x}}{\mathrm{1}−{x}}+\frac{\mathrm{14}{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{\mathrm{16}{x}^{\mathrm{3}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }+\frac{\mathrm{6}{x}^{\mathrm{4}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} }=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{n}\left({n}+\mathrm{1}\right)^{\mathrm{2}} {x}^{{n}} \\ $$$${set}\:{x}=\frac{\mathrm{1}}{\mathrm{10}}<\mathrm{1} \\ $$$$\frac{\mathrm{4}}{\mathrm{9}}+\frac{\mathrm{14}}{\mathrm{9}^{\mathrm{2}} }+\frac{\mathrm{16}}{\mathrm{9}^{\mathrm{3}} }+\frac{\mathrm{6}}{\mathrm{9}^{\mathrm{4}} }=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}\left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{10}^{{n}} } \\ $$$$\frac{\mathrm{6}+\mathrm{16}×\mathrm{9}+\mathrm{14}×\mathrm{9}^{\mathrm{2}} +\mathrm{4}×\mathrm{9}^{\mathrm{3}} }{\mathrm{9}^{\mathrm{4}} }=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}\left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{10}^{{n}} } \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}\left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{10}^{{n}} }=\frac{\mathrm{1400}}{\mathrm{2187}} \\ $$
Commented by Algoritm last updated on 05/Aug/20
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *