Menu Close

Question-106396

Tinku Tara 0 Comments
Pin




Question Number 106396 by I want to learn more last updated on 05/Aug/20
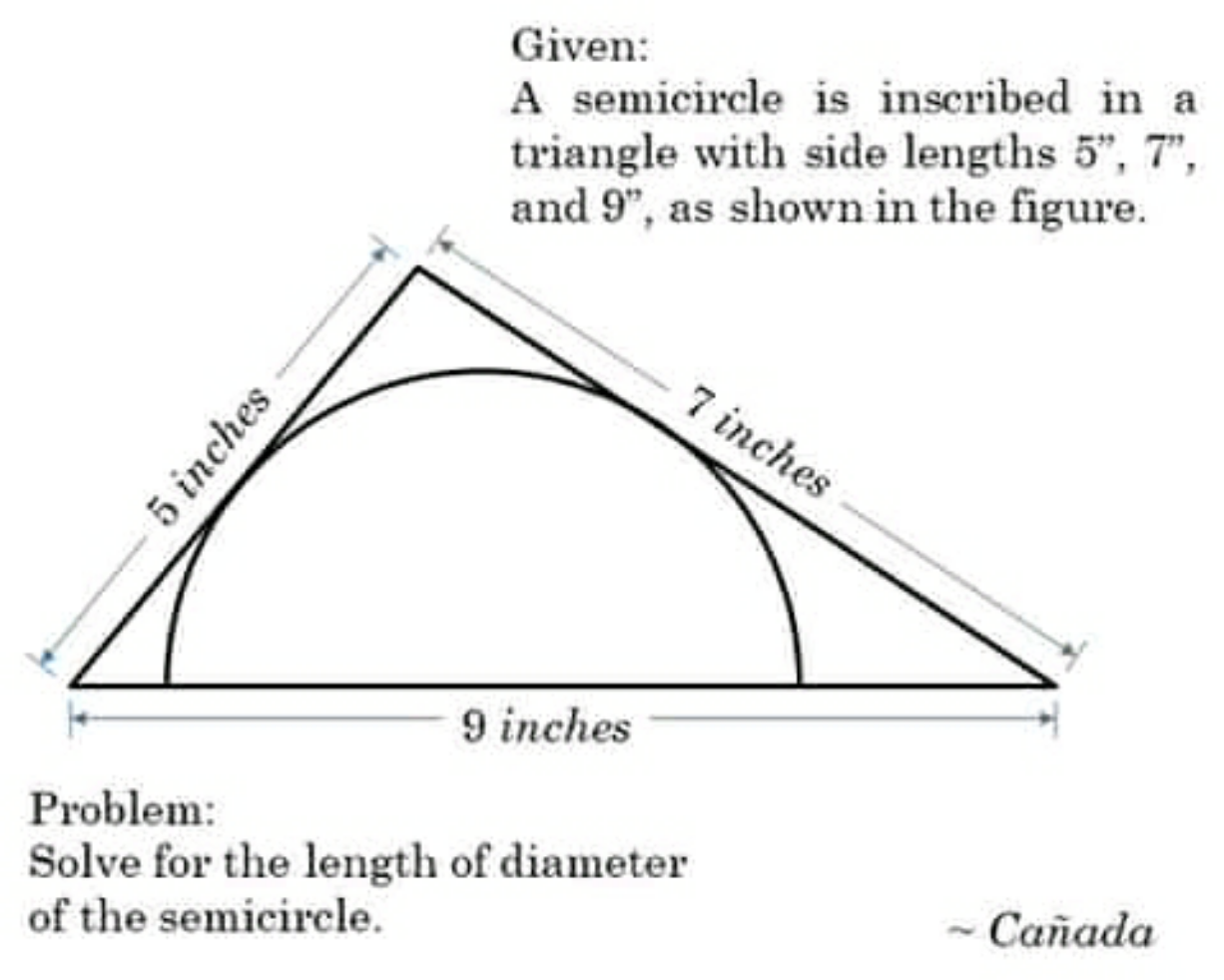
Commented by john santu last updated on 05/Aug/20
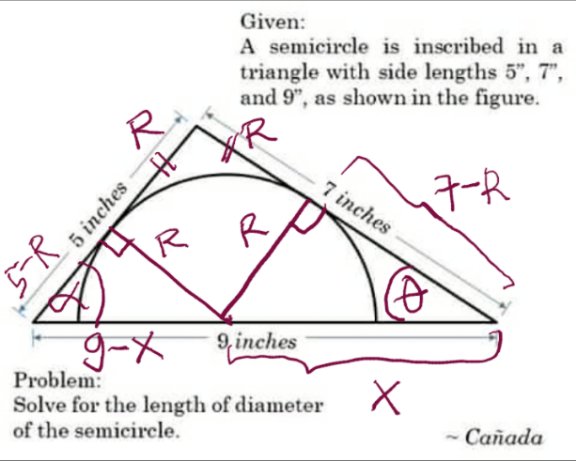
Commented by john santu last updated on 05/Aug/20
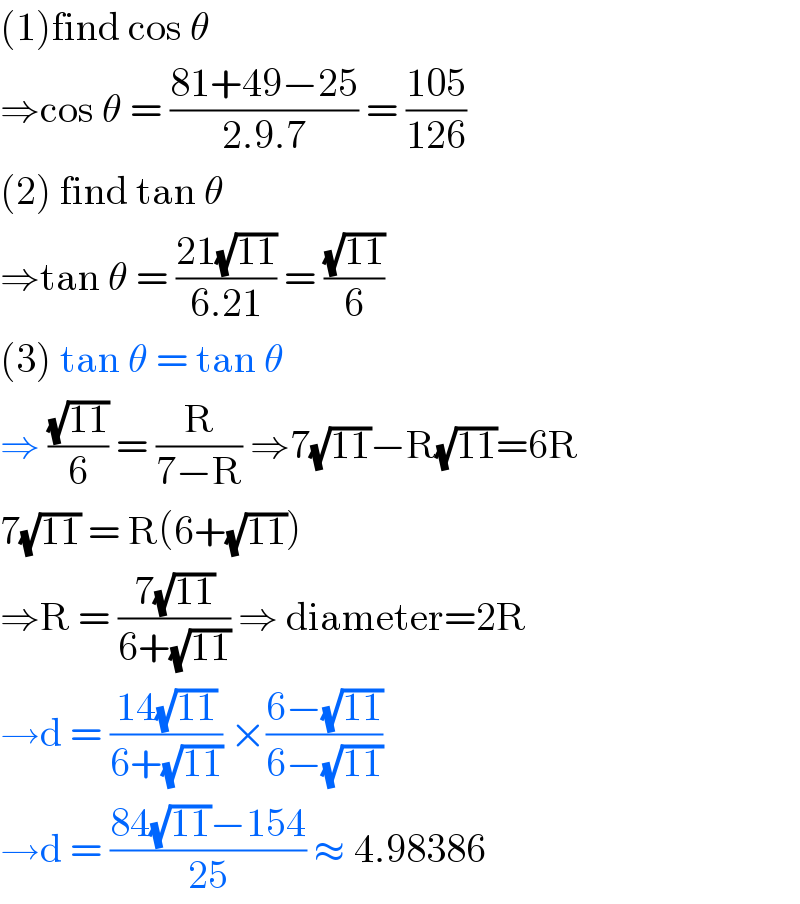
(1)find cos θ ⇒cos θ = ((81+49−25)/(2.9.7)) = ((105)/(126)) (2) find tan θ ⇒tan θ = ((21(√(11)))/(6.21)) = ((√(11))/6) (3) tan θ = tan θ ⇒ ((√(11))/6) = (R/(7−R)) ⇒7(√(11))−R(√(11))=6R 7(√(11)) = R(6+(√(11))) ⇒R = ((7(√(11)))/(6+(√(11)))) ⇒ diameter=2R →d = ((14(√(11)))/(6+(√(11)))) ×((6−(√(11)))/(6−(√(11)))) →d = ((84(√(11))−154)/(25)) ≈ 4.98386
$$\left(\mathrm{1}\right)\mathrm{find}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow\mathrm{cos}\:\theta\:=\:\frac{\mathrm{81}+\mathrm{49}−\mathrm{25}}{\mathrm{2}.\mathrm{9}.\mathrm{7}}\:=\:\frac{\mathrm{105}}{\mathrm{126}} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{find}\:\mathrm{tan}\:\theta \\ $$$$\Rightarrow\mathrm{tan}\:\theta\:=\:\frac{\mathrm{21}\sqrt{\mathrm{11}}}{\mathrm{6}.\mathrm{21}}\:=\:\frac{\sqrt{\mathrm{11}}}{\mathrm{6}} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{tan}\:\theta\:=\:\mathrm{tan}\:\theta\: \\ $$$$\Rightarrow\:\frac{\sqrt{\mathrm{11}}}{\mathrm{6}}\:=\:\frac{\mathrm{R}}{\mathrm{7}−\mathrm{R}}\:\Rightarrow\mathrm{7}\sqrt{\mathrm{11}}−\mathrm{R}\sqrt{\mathrm{11}}=\mathrm{6R} \\ $$$$\mathrm{7}\sqrt{\mathrm{11}}\:=\:\mathrm{R}\left(\mathrm{6}+\sqrt{\mathrm{11}}\right) \\ $$$$\Rightarrow\mathrm{R}\:=\:\frac{\mathrm{7}\sqrt{\mathrm{11}}}{\mathrm{6}+\sqrt{\mathrm{11}}}\:\Rightarrow\:\mathrm{diameter}=\mathrm{2R} \\ $$$$\rightarrow\mathrm{d}\:=\:\frac{\mathrm{14}\sqrt{\mathrm{11}}}{\mathrm{6}+\sqrt{\mathrm{11}}}\:×\frac{\mathrm{6}−\sqrt{\mathrm{11}}}{\mathrm{6}−\sqrt{\mathrm{11}}} \\ $$$$\rightarrow\mathrm{d}\:=\:\frac{\mathrm{84}\sqrt{\mathrm{11}}−\mathrm{154}}{\mathrm{25}}\:\approx\:\mathrm{4}.\mathrm{98386} \\ $$
Commented by I want to learn more last updated on 05/Aug/20
Thanks sir
$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Answered by 1549442205PVT last updated on 05/Aug/20
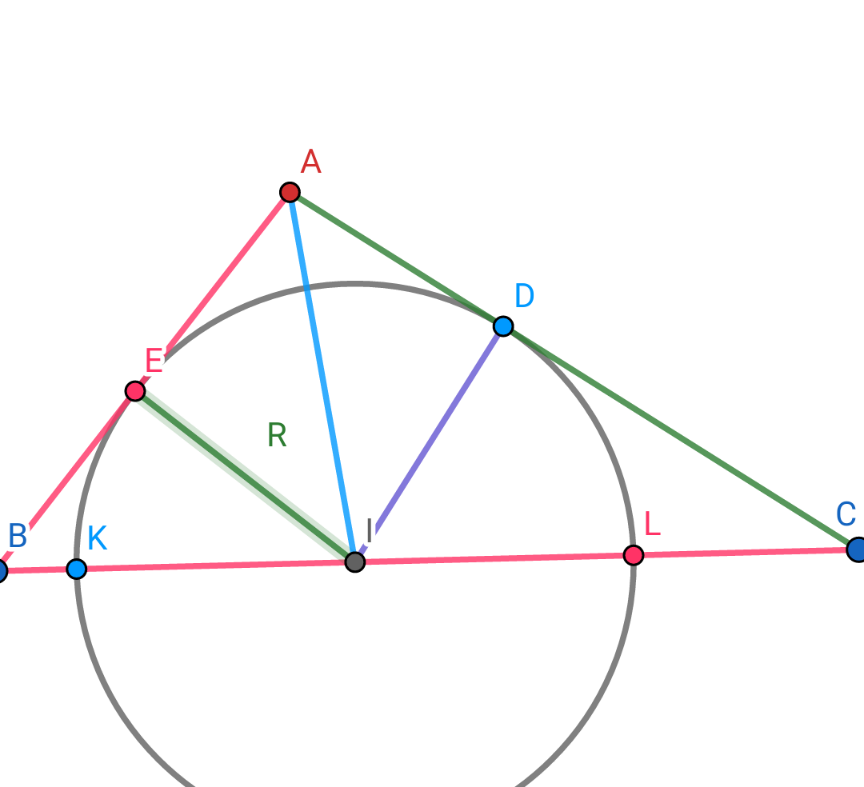
Commented by 1549442205PVT last updated on 06/Aug/20
Apply the cosine for ΔABC withBC=a AC=b,AB=c we find out cosB=((a^2 +c^2 −b^2 )/(2ac))=((81+25−49)/(90))=((19)/(30)) ⇒tanB=(√((1/(cos^2 B))−1))=(√(((900)/(361))−1))=(√((539)/(361)))=((7(√(11)))/(19)) cosA=((b^2 +c^2 −a^2 )/(2bc))=((25+49−81)/(70))=((−1)/(10)) Since the center I of the circle lie on BC ,AI be the bisector of the angle A⇒BAI^(�) =(A/2) ⇒cos(A/2)=(√((1+cosA)/2))=(√(9/(20))) ⇒tan(A/2)=(√((1+cos(A/2))/2))=(√(((20)/9)−1))=((√(11))/3) AB=5=AE+BE=(R/(tan(A/2)))+(R/(tanB))=R((3/( (√(11))))+((19)/(7(√(11))))) ⇒R=(5/((3/( (√(11))))+((19)/(7(√(11))))))=((7(√(11)))/8)⇒d=2R=((7(√(11)))/4) Thus,the diameter of the circle equal to KL=((7(√(11)))/4)≈5.8 other way: From the proper ty of the bisectors in the triangle we have ((IB)/(AB))=((IC)/(AC)) ⇒((IB)/c)=((IC)/b)=(a/(b+c))⇒IB=((ac)/(b+c))=((9.5)/(7+5))=((45)/(12))=((15)/4) ⇒R=IE=IB×sinB=((45)/(12))×(√(1−(((19)/(30)))^2 )) =((15)/4)×(√((539)/(361)))=((15)/4)×(7/(30))(√(11))=((7(√(11)))/8) ⇒d=2R=((7(√(11)))/4)
$$\mathrm{Apply}\:\mathrm{the}\:\mathrm{cosine}\:\mathrm{for}\:\Delta\mathrm{ABC}\:\mathrm{withBC}=\mathrm{a} \\ $$$$\mathrm{AC}=\mathrm{b},\mathrm{AB}=\mathrm{c}\:\mathrm{we}\:\mathrm{find}\:\mathrm{out} \\ $$$$\mathrm{cosB}=\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }{\mathrm{2ac}}=\frac{\mathrm{81}+\mathrm{25}−\mathrm{49}}{\mathrm{90}}=\frac{\mathrm{19}}{\mathrm{30}} \\ $$$$\Rightarrow\mathrm{tanB}=\sqrt{\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \mathrm{B}}−\mathrm{1}}=\sqrt{\frac{\mathrm{900}}{\mathrm{361}}−\mathrm{1}}=\sqrt{\frac{\mathrm{539}}{\mathrm{361}}}=\frac{\mathrm{7}\sqrt{\mathrm{11}}}{\mathrm{19}} \\ $$$$\mathrm{cosA}=\frac{\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }{\mathrm{2bc}}=\frac{\mathrm{25}+\mathrm{49}−\mathrm{81}}{\mathrm{70}}=\frac{−\mathrm{1}}{\mathrm{10}} \\ $$$$\mathrm{Since}\:\mathrm{the}\:\mathrm{center}\:\mathrm{I}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{lie}\:\mathrm{on}\:\mathrm{BC} \\ $$$$,\mathrm{AI}\:\mathrm{be}\:\mathrm{the}\:\mathrm{bisector}\:\mathrm{of}\:\mathrm{the}\:\mathrm{angle}\:\mathrm{A}\Rightarrow\widehat {\mathrm{BAI}}=\frac{\mathrm{A}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{cos}\frac{\mathrm{A}}{\mathrm{2}}=\sqrt{\frac{\mathrm{1}+\mathrm{cosA}}{\mathrm{2}}}=\sqrt{\frac{\mathrm{9}}{\mathrm{20}}} \\ $$$$\Rightarrow\mathrm{tan}\frac{\mathrm{A}}{\mathrm{2}}=\sqrt{\frac{\mathrm{1}+\mathrm{cos}\frac{\mathrm{A}}{\mathrm{2}}}{\mathrm{2}}}=\sqrt{\frac{\mathrm{20}}{\mathrm{9}}−\mathrm{1}}=\frac{\sqrt{\mathrm{11}}}{\mathrm{3}} \\ $$$$\mathrm{AB}=\mathrm{5}=\mathrm{AE}+\mathrm{BE}=\frac{\mathrm{R}}{\mathrm{tan}\frac{\mathrm{A}}{\mathrm{2}}}+\frac{\mathrm{R}}{\mathrm{tanB}}=\mathrm{R}\left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{11}}}+\frac{\mathrm{19}}{\mathrm{7}\sqrt{\mathrm{11}}}\right) \\ $$$$\Rightarrow\mathrm{R}=\frac{\mathrm{5}}{\frac{\mathrm{3}}{\:\sqrt{\mathrm{11}}}+\frac{\mathrm{19}}{\mathrm{7}\sqrt{\mathrm{11}}}}=\frac{\mathrm{7}\sqrt{\mathrm{11}}}{\mathrm{8}}\Rightarrow\mathrm{d}=\mathrm{2R}=\frac{\mathrm{7}\sqrt{\mathrm{11}}}{\mathrm{4}} \\ $$$$\mathrm{Thus},\mathrm{the}\:\mathrm{diameter}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{equal} \\ $$$$\mathrm{to}\:\mathrm{KL}=\frac{\mathrm{7}\sqrt{\mathrm{11}}}{\mathrm{4}}\approx\mathrm{5}.\mathrm{8} \\ $$$$\boldsymbol{\mathrm{other}}\:\boldsymbol{\mathrm{way}}:\: \\ $$$$\mathrm{From}\:\mathrm{the}\:\mathrm{proper}\:\mathrm{ty}\:\mathrm{of}\:\mathrm{the}\:\mathrm{bisectors}\:\mathrm{in} \\ $$$$\mathrm{the}\:\mathrm{triangle}\:\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{IB}}{\mathrm{AB}}=\frac{\mathrm{IC}}{\mathrm{AC}} \\ $$$$\Rightarrow\frac{\mathrm{IB}}{\mathrm{c}}=\frac{\mathrm{IC}}{\mathrm{b}}=\frac{\mathrm{a}}{\mathrm{b}+\mathrm{c}}\Rightarrow\mathrm{IB}=\frac{\mathrm{ac}}{\mathrm{b}+\mathrm{c}}=\frac{\mathrm{9}.\mathrm{5}}{\mathrm{7}+\mathrm{5}}=\frac{\mathrm{45}}{\mathrm{12}}=\frac{\mathrm{15}}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{R}=\mathrm{IE}=\mathrm{IB}×\mathrm{sinB}=\frac{\mathrm{45}}{\mathrm{12}}×\sqrt{\mathrm{1}−\left(\frac{\mathrm{19}}{\mathrm{30}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{15}}{\mathrm{4}}×\sqrt{\frac{\mathrm{539}}{\mathrm{361}}}=\frac{\mathrm{15}}{\mathrm{4}}×\frac{\mathrm{7}}{\mathrm{30}}\sqrt{\mathrm{11}}=\frac{\mathrm{7}\sqrt{\mathrm{11}}}{\mathrm{8}} \\ $$$$\Rightarrow\boldsymbol{\mathrm{d}}=\mathrm{2}\boldsymbol{\mathrm{R}}=\frac{\mathrm{7}\sqrt{\mathrm{11}}}{\mathrm{4}} \\ $$
Commented by I want to learn more last updated on 05/Aug/20
Thanks sir, but two of you have different answers sir.
$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{but}\:\mathrm{two}\:\mathrm{of}\:\mathrm{you}\:\mathrm{have}\:\mathrm{different}\:\mathrm{answers}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *