Question Number 106444 by mathdave last updated on 05/Aug/20
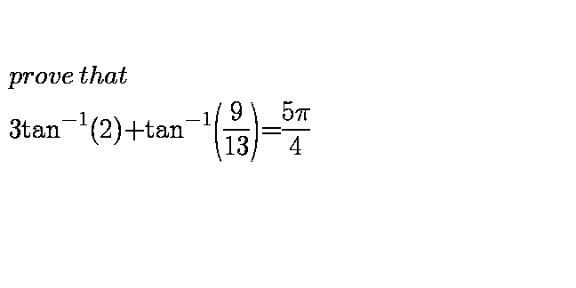
Answered by nimnim last updated on 05/Aug/20
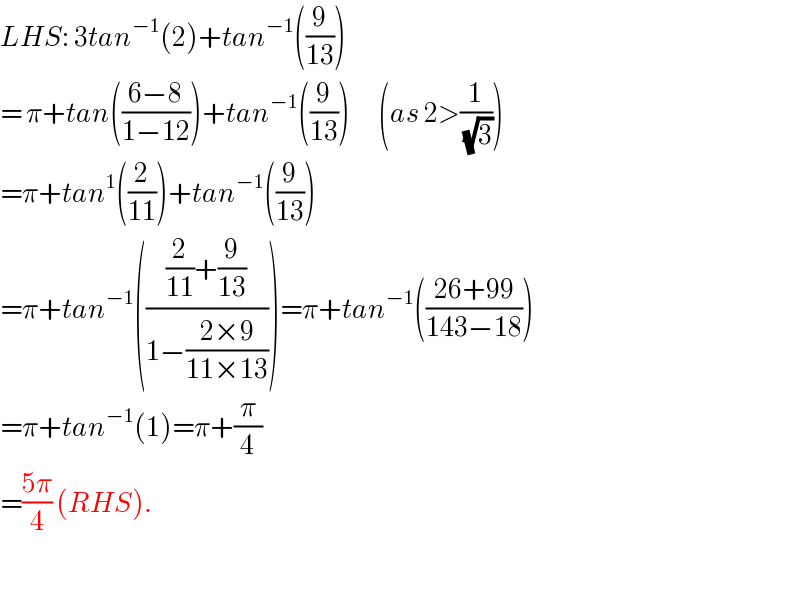
$${LHS}:\:\mathrm{3}{tan}^{−\mathrm{1}} \left(\mathrm{2}\right)+{tan}^{−\mathrm{1}} \left(\frac{\mathrm{9}}{\mathrm{13}}\right) \\ $$$$=\:\pi+{tan}\left(\frac{\mathrm{6}−\mathrm{8}}{\mathrm{1}−\mathrm{12}}\right)+{tan}^{−\mathrm{1}} \left(\frac{\mathrm{9}}{\mathrm{13}}\right)\:\:\:\:\:\:\:\left({as}\:\mathrm{2}>\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right) \\ $$$$=\pi+{tan}^{\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{11}}\right)+{tan}^{−\mathrm{1}} \left(\frac{\mathrm{9}}{\mathrm{13}}\right) \\ $$$$=\pi+{tan}^{−\mathrm{1}} \left(\frac{\frac{\mathrm{2}}{\mathrm{11}}+\frac{\mathrm{9}}{\mathrm{13}}}{\mathrm{1}−\frac{\mathrm{2}×\mathrm{9}}{\mathrm{11}×\mathrm{13}}}\right)=\pi+{tan}^{−\mathrm{1}} \left(\frac{\mathrm{26}+\mathrm{99}}{\mathrm{143}−\mathrm{18}}\right) \\ $$$$=\pi+{tan}^{−\mathrm{1}} \left(\mathrm{1}\right)=\pi+\frac{\pi}{\mathrm{4}} \\ $$$$=\frac{\mathrm{5}\pi}{\mathrm{4}}\:\left({RHS}\right). \\ $$$$ \\ $$
Commented by mathdave last updated on 05/Aug/20

$${thank} \\ $$
Commented by mathdave last updated on 05/Aug/20
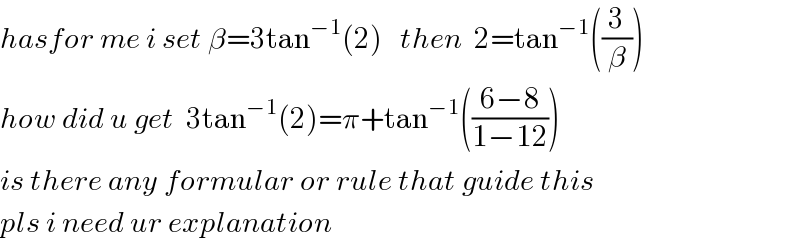
$${hasfor}\:{me}\:{i}\:{set}\:\beta=\mathrm{3tan}^{−\mathrm{1}} \left(\mathrm{2}\right)\:\:\:{then}\:\:\mathrm{2}=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\beta}\right) \\ $$$${how}\:{did}\:{u}\:{get}\:\:\mathrm{3tan}^{−\mathrm{1}} \left(\mathrm{2}\right)=\pi+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{6}−\mathrm{8}}{\mathrm{1}−\mathrm{12}}\right) \\ $$$${is}\:{there}\:{any}\:{formular}\:{or}\:{rule}\:{that}\:{guide}\:{this} \\ $$$${pls}\:{i}\:{need}\:{ur}\:{explanation} \\ $$
Commented by mathdave last updated on 05/Aug/20
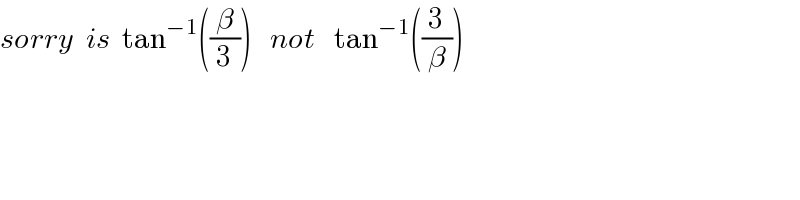
$${sorry}\:\:{is}\:\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\beta}{\mathrm{3}}\right)\:\:\:{not}\:\:\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\beta}\right) \\ $$
Commented by nimnim last updated on 05/Aug/20
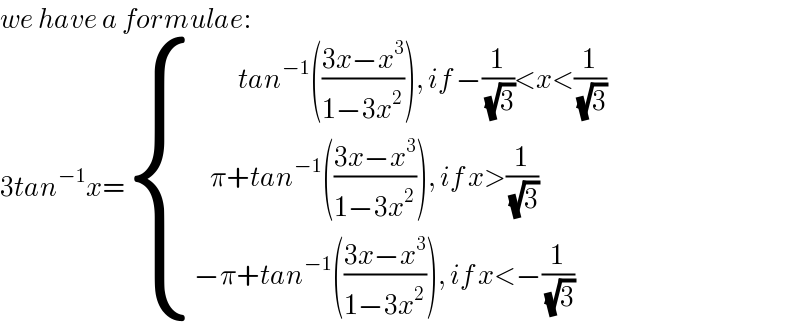
$${we}\:{have}\:{a}\:{formulae}: \\ $$$$\mathrm{3}{tan}^{−\mathrm{1}} {x}=\begin{cases}{\:\:\:\:\:\:\:\:\:\:\:{tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}{x}−{x}^{\mathrm{3}} }{\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} }\right),\:{if}\:−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}<{x}<\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}\\{\:\:\:\:\pi+{tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}{x}−{x}^{\mathrm{3}} }{\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} }\right),\:{if}\:{x}>\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}\\{−\pi+{tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}{x}−{x}^{\mathrm{3}} }{\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} }\right),\:{if}\:{x}<−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}\end{cases} \\ $$
Commented by mathdave last updated on 05/Aug/20
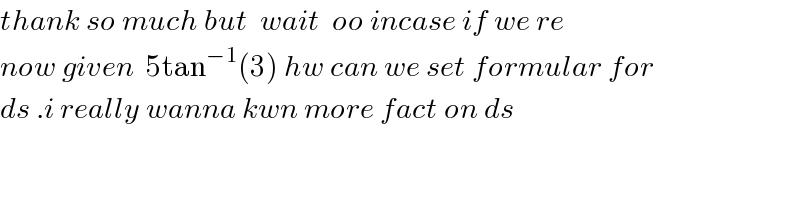
$${thank}\:{so}\:{much}\:{but}\:\:{wait}\:\:{oo}\:{incase}\:{if}\:{we}\:{re} \\ $$$${now}\:{given}\:\:\mathrm{5tan}^{−\mathrm{1}} \left(\mathrm{3}\right)\:{hw}\:{can}\:{we}\:{set}\:{formular}\:{for} \\ $$$${ds}\:.{i}\:{really}\:{wanna}\:{kwn}\:{more}\:{fact}\:{on}\:{ds} \\ $$
